Операторы квантовой механики и среднее значение
В квантовой механике можно говорить лишь о вероятности того или другого значения динамической переменной и спектр физической величины в общем случае является дискретным. Чтобы отобразить эти свойства, используются не самые динамические переменные, а описующие их операторы.
Оператором
называется правило, с помощью которого
каждой функции
из некоторого множества функций ставится
в соответствие функция
из того же или некоторого другого
множества функций. Символическая запись
имеет такой вид
.
(1.9)
В квантовой механике, чтобы удовлетворить принципу суперпозиции, употребляются лишь линейные операторы, то есть такие, для которых имеет место равенство
,
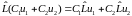где
и
есть какие-либо функции из множества,
а
и
произвольные постоянные.
Произведение
двух линейных операторов
и
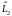определяется как
,
если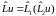
.
Если
произведение не зависит от порядка
сомножителей, то операторы называются
коммутирующими
.
Функция называется собственной функцией оператора, если после действия на нее оператором выходит та же функция с точностью до постоянного множителя
.
(1.10)
Решение
этого уравнения существуют только для
специальных значений
,
которые называются собственными
значениями оператора
.
Собственные значения называются
невырожденными, если каждому из них
отвечает лишь одна собственная функция.
В противном случае собственные значения
называются вырожденными.
В квантовой механике используются лишь эрмитовы (линейные самосопряженные) операторы. Это связано с их главным свойством: собственные значения таких операторов действительны.
Оператор является эрмитовым, если для любых двух функций и имеет место соотношение
,
(1.11))
где произведение определяется как
.
Система собственных функций эрмитова оператора является полной ортогональной системой функций. Поскольку собственные функции определяются с точностью до постоянного множителя, то их можно нормировать. Условие ортогональности и нормировки записывается в виде
.
(1.12)
Вследствие полноты системы собственных функций любая функция может быть представлена в виде разложения по собственным функциям
,
(1.13)
где коэффициенты – постоянные числа и определяются
.
(1.14)
В классической механике каждая динамическая переменная имеет определенное значение. Им является число, которое мы получим при измерении величины, которая нас интересует. Это число мы получаем при измерении каждый раз, если система находится в одном и том же состоянии.
Другое
дело в квантовой механике. Как мы выяснили
выше (см. разд. 1.4), если система находится
в состоянии
,
который представляет суперпозицию
состояний
и
с
собственными значениями
и
соответственно,
то при измерении динамической переменной,
оператор которой
,
мы получим или число
,
или
.
Причем заранее невозможно предвидеть
к которому из чисел приведет измерение:
в одних случаях мы будем получать
,
во других –
.
То или иное значение получается не с
достоверностью, а лишь с определенной
вероятностью. Это означает, что процесс
измерения влияет на систему: до измерения
система находилась в состоянии
,
после измерения она переходит или в
состояние
или
в состояние
(см.
разд.1.4).
Таким образом, динамической переменной в квантовой механике невозможно приписать определенное значение, но возможно приписать определенную вероятность получения данного значения в результате измерения. А если известны вероятности, то можно вычислить и среднее значение.
Среднее значение динамической переменной, которая описывается оператором , для системы в состоянии определяется за формулой
(1.15)
при условии, что волновая функция нормирована на единицу.
Таким образом, в квантовой механике каждая динамическая переменная описывается эрмитовым оператором. Выбор конкретного вида оператора определяется соответствием полученных с его помощью результатов с экспериментом. Ниже приводятся некоторые важнейшие операторы квантовой механики.
Оператор координаты.
Волновая функция рассматривается нами как координата частицы, поэтому оператор координаты есть сама координата
.
(1.16)
Действие
функции координат частицы
как оператора сводится просто к умножению
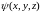на
.
Операторы импульса и проекции импульса.
При таком выборе переменных для волновой функции операторы проекций импульса имеют вид
,
(1.17)
а оператор импульса в векторной форме
,
(1.18)
где
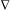– оператор градиента (набла).
Операторы проекций импульса и координат подчиняются определенным правилам перестановки, которые облегчают расчеты с ними.
Если есть волновая функция, то имеем
Отнимая вторую сроку от первой, получим
Следовательно, отсюда можем записать
(1.19)
Это так называемые перестановочные соотношения Гайзенберга.
Следовательно,
(1.20)
Аналогичным образом устанавливаются наиболее общие перестановочные соотношения любой функции и операторов импульса
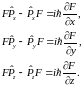(1.21)
Из соотношений (1.19) вытекает, что не существует состояний, в которых импульс и соответствующая ему координата имеют одновременно определенные значения. Уравнение (1.19) и (1.21) в операторной форме выражают известное соотношение Гайзенберга.
Оператор момента импульса и его проекций
Моментом импульса частицы (моментом количества движения) в классической механике называют векторное произведение радиус-вектора на импульс
.
(1.22)
Значение этой величины определяется тем, что она является интегралом движения в поле центральных сил.
В квантовой механике момент импульса задается оператором
.
(1.23)
Операторы проекций момента импульса на оси координат имеют вид
(1.24)
Из (1.24) можно получить перестановки
(1.25)
Таким
образом, операторы компонент момента
импульса некоммутативны, из чего
выплывает, что проекции момента импульса
нельзя одновременно измерить.
Важным в квантовой механике является оператор квадрата момента импульса
.
(1.26)
Каждая из компонент момента импульса коммутирует с квадратом полного момента импульса. Например,
.
(1.27)
Для решения некоторых задач квантовой механики удобнее пользоваться сферической системой координат. В этой системе
(1.28)
где
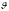– угол между
осью
и радиус-вектором
,
а
– угол, что отчисляется в плоскости
от оси
.
В
этой системе операторы
и
имеют вид
(1.29)
(1.30)
где
– сферический оператор Лапласа
.
(1.31)
Оператор энергии и функции Гамильтона
Опыт
показывает, что кинетическая энергия
микрочастиц связана с импульсом таким
же образом, как и для макроскопических
тел. Из этого обстоятельства вытекает,
что оператор кинетической энергии
частицы с массой
будет иметь вид
.
(1.32)
Воспользовавшись (1.17), получим
,
(1.33)
где
–
оператор Лапласа. В сферической системе
координат этот оператор будет имеет
вид
.
(1.34)
Воспользовавшись (1.33), (1.34) и (1.30), мы получим
,
(1.35)
где
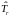– оператор кинетической энергии,
соответствует движению частицы вдоль
радиуса-вектора
.
(1.36)
Оператор
полной энергии
есть сумма операторов кинетической
и потенциальной
энергий. Поскольку последняя представляет
собой функцию только координат частицы,
то оператор
есть
просто
.
Следовательно,
.
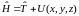(1.37)
Потенциальная энергия характеризует силовое поле, которая действует на частицу, и ее вид заимствуется из опыта.
В квантовой механике нельзя утверждать, что полная энергия представляет собой сумму кинетической и потенциальной энергий, поскольку кинетическая энергия есть функция импульсов, а потенциальная – координат. И не существует таких состояний квантовой системы, в которых частицы имели бы одновременно определенные импульсы и координаты (соотношение неопределенностей).
Следовательно, нельзя измерить полную энергию частицы, отдельно измеряя ее кинетическую и потенциальную энергии. Полная энергия измеряется как одно целое.
В классической механике полную энергию, которая представлена через импульсы и координаты, называют функцией Гамильтона. Поэтому в квантовой механике оператор также называют оператором функции Гамильтона или гамильтонианом.
В заключение этого раздела напомним, что одновременно могут быть измерены лишь такие динамические переменные, операторы которых коммутируют.