10

Глава 9. Металлы

§1. Модель свободных электронов

Первой удачной попыткой объяснения электрических и магнитных свойств твердых тел, в первую очередь металлов, явилась теория свободных электронов. Основное положение модели свободных электронов — валентные электроны атомов металла могут достаточно свободно перемещаться по объему кристалла. Эти электроны являются носителями электрического тока и поэтому их называют электронами проводимости. Они могут проходить расстояния, составляющие несколько периодов кристаллической решетки, не сталкиваясь друг с другом и ионными остовами, т.е. ведут себя как идеальный газ. Газ свободных невзаимодействующих электронов называется идеальным электронным газом Ферми.

В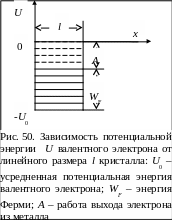 данной модели усредняются силы притяжения, действующие на валентный электрон со стороны ионных остовов. Следовательно, потенциальная энергия электрона — постоянная отрицательная величина. Таким образом, можно считать, что каждый валентный электрон движется в «потенциальной яме» глубиной , а металл объемом V рассматривать как «потенциальную яму» того же объема, содержащую N свободных электронов.

Для одного измерения зависимость потенциальной энергии валентного электрона от линейного размера кристалла имеет вид, представленный на рис. 50.

Электроны в яме будут занимать состояния в соответствии с принципом наименьшей энергии и принципом Паули.

Максимальный занятый энергетический уровень называется уровнем Ферми. Кинетическая энергия электрона, находящегося на уровне Ферми, называется энергией Ферми.

Найдем энергию Ферми для следующей физической модели: «потенциальной ямы» в форме куба со стороной l, в которой находится N электронов.

Кинетическая энергия W_k электрона равна:

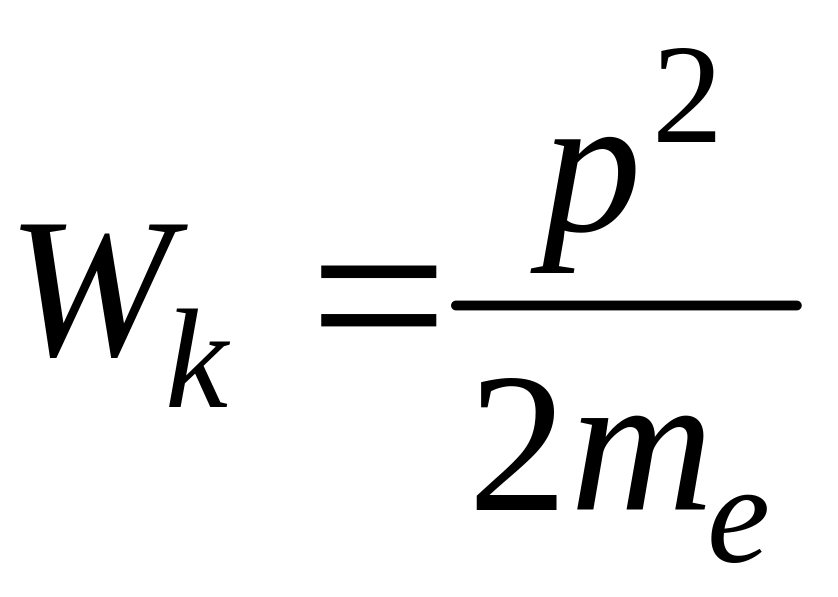, (1)

где p – импульс, – масса электрона.

Величина

, (2)

где , , – проекции импульса электрона на соответствующие координатные оси OX, OY, OZ.

Тогда

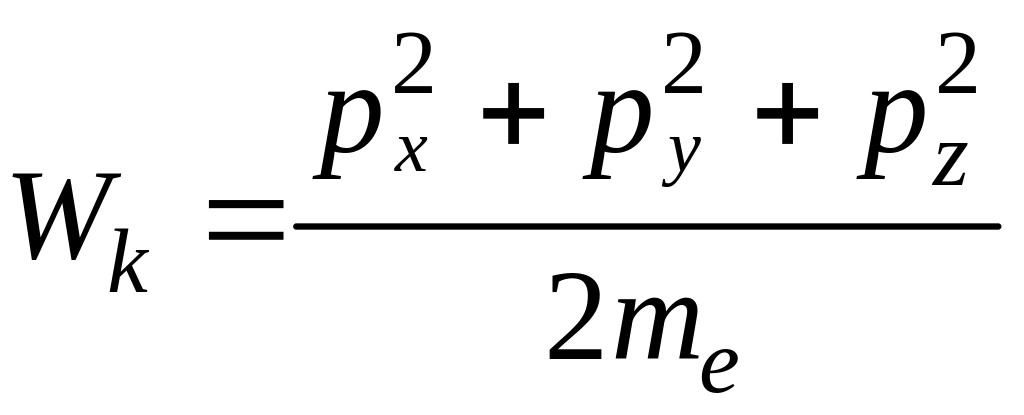. (3)

В соответствии с гипотезой де Бройля:

(4)

где , , – волновые числа вдоль осей OX, OY, OZ, соответственно.

Как было показано ранее, для одномерной «потенциальной ямы»

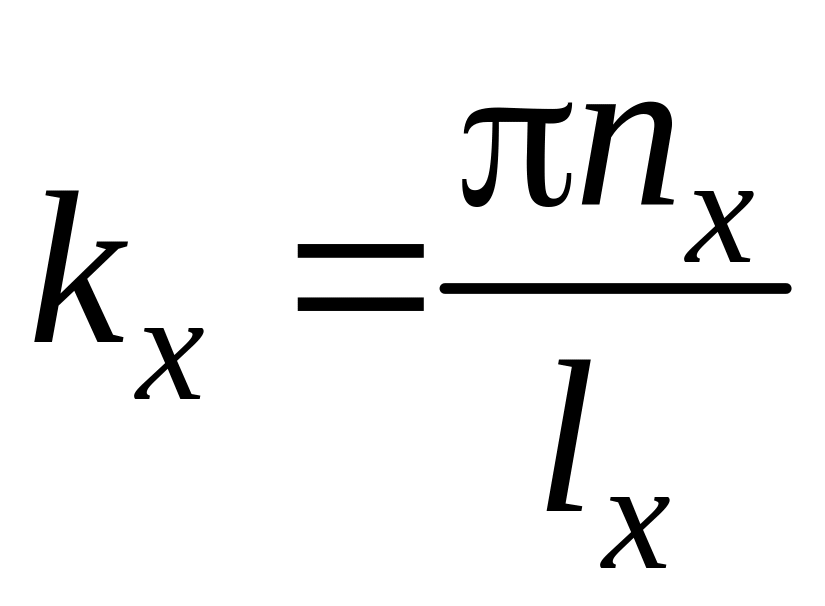, (5)

где – главное квантовое число, – ширина «ямы» в направлении оси ОХ.

Аналогичные соотношения можно записать для и .

Тогда

. (6)

Так как мы рассматриваем случай , то

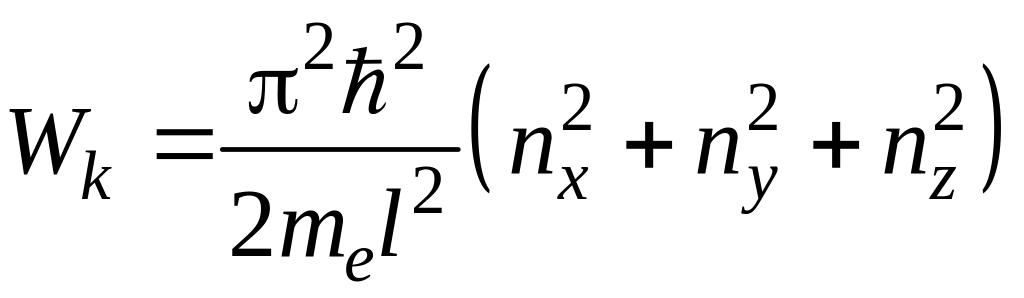, (7)

где , , - квантовые числа, определяющие энергию электрона в трехмерной яме.

В соответствии с Принципом Паули в состоянии с энергией, определяемой набором квантовых чисел , и , может находиться два электрона.

Чтобы найти W_F необходимо подсчитать число заполненных состояний. Найдем это число.

Из соотношений (4) и (5) с учетом следует:

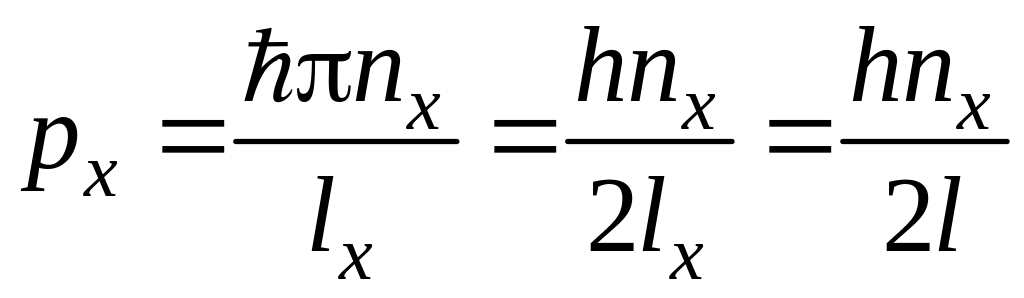; (8)

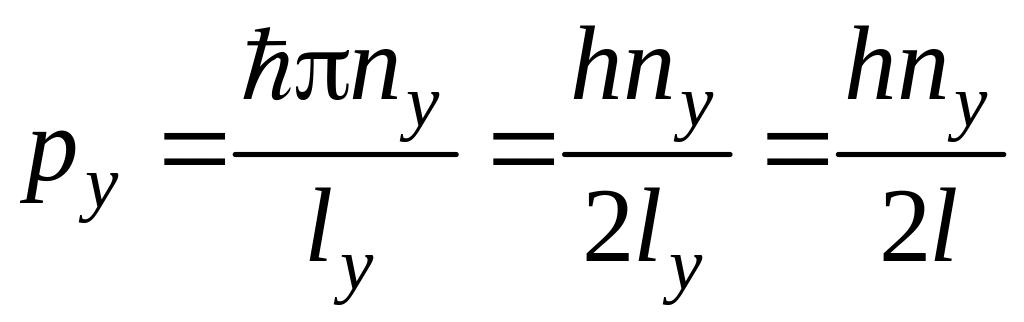; (9)

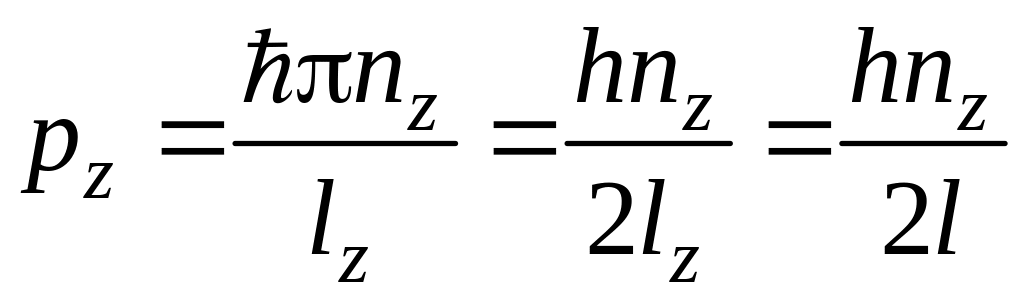. (10)

Обозначим через – импульс электрона, находящегося на уровне Ферми, тогда – максимально возможное значение для , , . Максимальные значения квантовых чисел , и равны:

. (11)

Таким образом, число заполненных состояний равно удвоенному числу возможных комбинаций , и , каждое из которых не превышает . Подсчитаем число возможных комбинаций , и . Каждое из таких состояний можно изобразить точкой в системе координат , и (рис. 51). Заполненные состояния находятся внутри сферического сегмента радиусом

. (12)

Т очки с координатами , и образуют кубическую решетку с ребром ячейки равным 1. Число кубических ячеек равно числу точек.

Тогда число состояний, определяемых числами , и , численно равно числу кубических ячеек, ограниченных сферической поверхностью.

С учетом принципа Паули полное число N заполненных состояний (или полное число электронов):

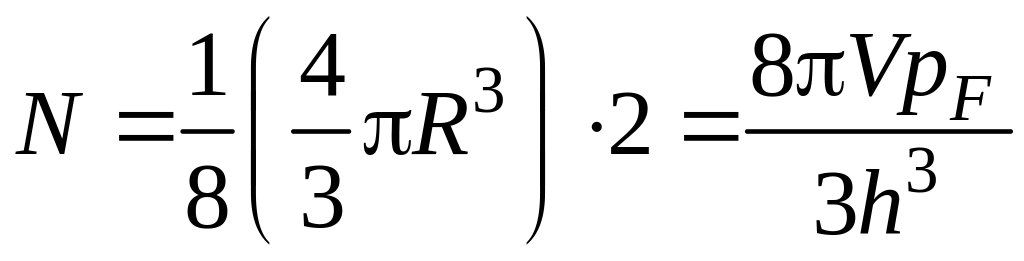, (13)

где – объем кристалла.

Из соотношения (13) находим импульс Ферми:

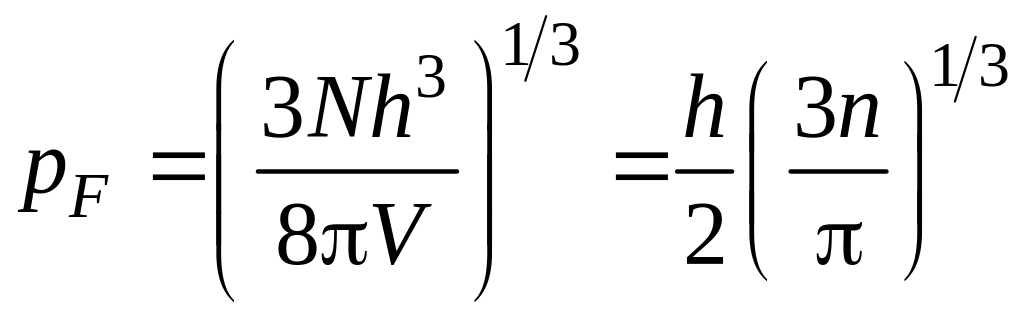, (14)

тогда энергия Ферми:

, (15)

где n – концентрация электронов; – масса электрона.

Таким образом, зависит только от концентрации электронов в металле.

Минимальная энергия, необходимая для удаления электрона из металла, называется работой выхода A:

. (16)

Основное состояние системы электронов — это состояние при температуре . При повышениии температуры кинетическая энергия электронов увеличивается; при этом электроны будут занимать состояния с энергиями . Состояния, которые эти электроны занимали при , становятся вакантными.

Как отмечалось ранее, вероятность того, что в состоянии теплового равновесия идеального газа при температуре T состояние с энергией занято электроном, определяется функцией Ферми-Дирака:

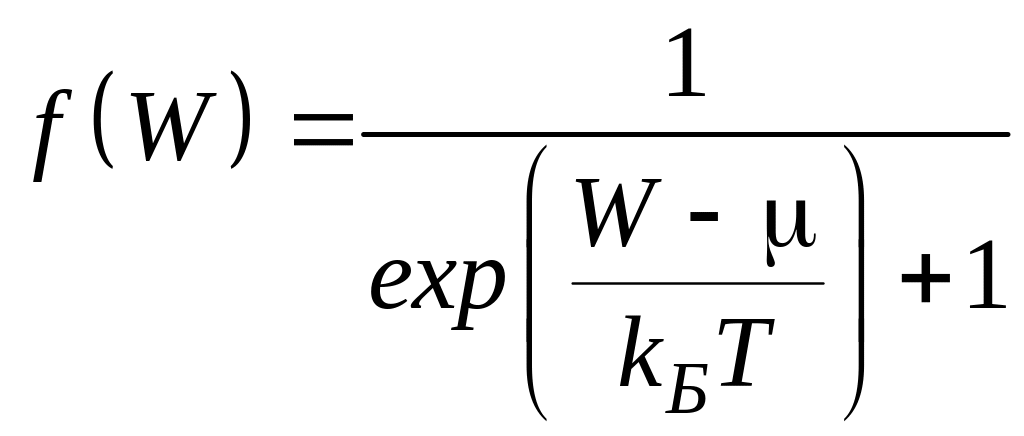. (17)

Г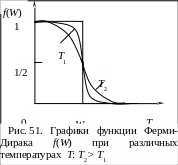 рафики зависимостей при различных температурах T приведены на рис. 52.

При температуре , следовательно,

. (18)

Если , то из (18) следует, что . Таким образом, вероятность заполнения уровня Ферми при любой температуре одинакова и равна .

Газ электронов, подчиняющийся статистике Ферми-Дирака, называется вырожденным.

Если в выражении (18) 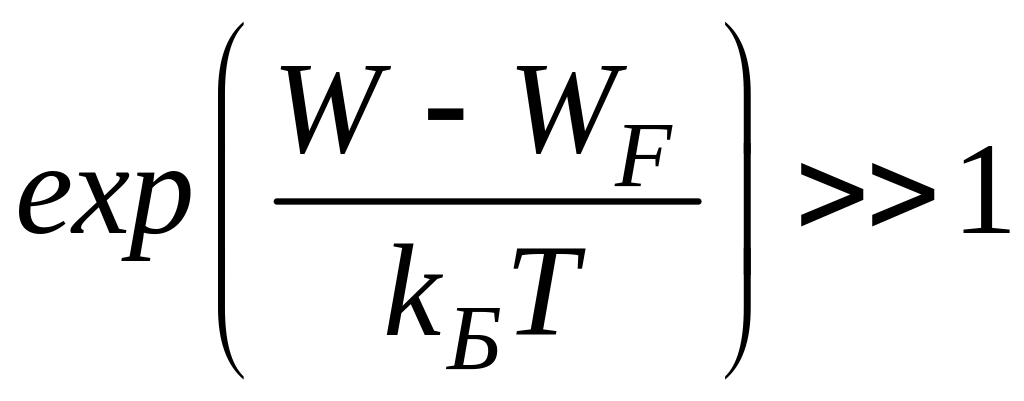, то

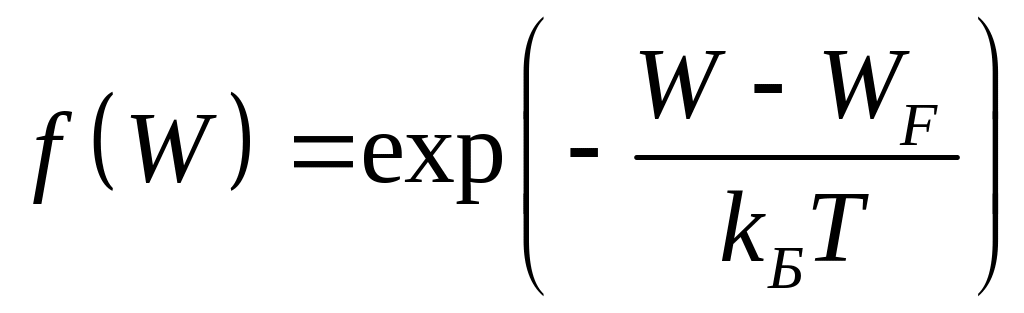, (19)

т.е. распределение Ферми-Дирака переходит в распределение Максвелла-Больцмана. В этом случае поведение газа описывается законами классической статистики, а сам газ называется невырожденным.

Модель свободных электронов позволила установить температурную зависимость электропроводности и теплопроводности, правильно оценить их абсолютную величину, описать широкий круг явлений, связанный с эмиссией электронов, термоэлектрическими явлениями, магнитными свойствами металлов и т.д. Рассмотрим некоторые применения этой теории.