
- •13 Лекция 6 14.03.2007
- •Переход от ду высшего порядка к сду первого порядка.
- •Использование вычислительной системы mathcad
- •График решения
- •Решение систем оду в одной заданной точке
- •Аналитические методы решения ду. Метод последовательного дифференцирования
- •Метод последовательных приближений ( метод Пикара) .
Аналитические методы решения ду. Метод последовательного дифференцирования
Рассмотрим задачу Коши в общем виде
![]()
с начальными
условиями
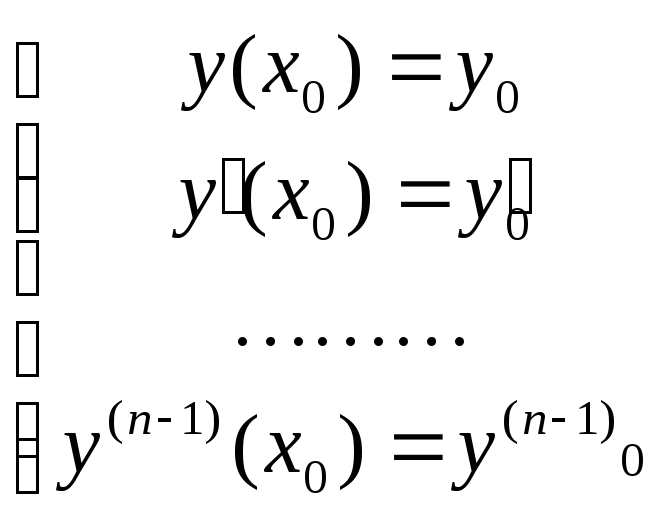
Предположим , что искомое частное решение y(x) может быть разложено в ряд Тейлора по степеням разности (x-x0).
![]()
Начальные условия
дадут
![]()
Значение для
![]() найдем
из уравнения задачи Коши , подставляя
начальные условия
найдем
из уравнения задачи Коши , подставляя
начальные условия
![]()
Величины
![]() ,
,
![]() ,…
определятся аналогично.
,…
определятся аналогично.
Доказано : Если правая часть уравнения задачи Коши в окрестности точки
![]() есть аналитическая
функция своих аргументов, то при значениях
x
, близких к значению x0
, существует единственное решение задачи
Коши, которое разлагается в ряд Тейлора
. Тогда частичная сумма этого ряда будет
приближенным решением поставленной
задачи Коши.
есть аналитическая
функция своих аргументов, то при значениях
x
, близких к значению x0
, существует единственное решение задачи
Коши, которое разлагается в ряд Тейлора
. Тогда частичная сумма этого ряда будет
приближенным решением поставленной
задачи Коши.
Аналогично данный метод применяется и для решения систем ОДУ .
Рассмотрим пример :
Найти первые четыре члена разложения в степенной ряд решения y=y(x) и z=z(x) системы
![]() с начальными
с начальными
![]()
Функции ищем в виде степенных рядов:
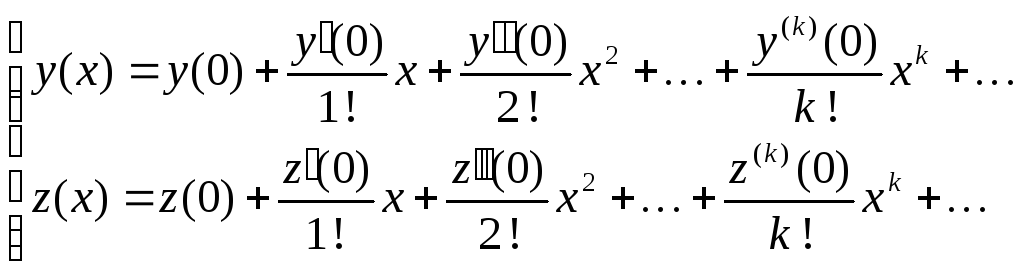
-
Положив x=0 имеем

-
Для вторых производных
![]()
Находим
![]()
-
Далее имеем
![]()
Находим
![]()
Подставляя полученные величины в ряды , получаем разложение вплоть до четвертого слагаемого :
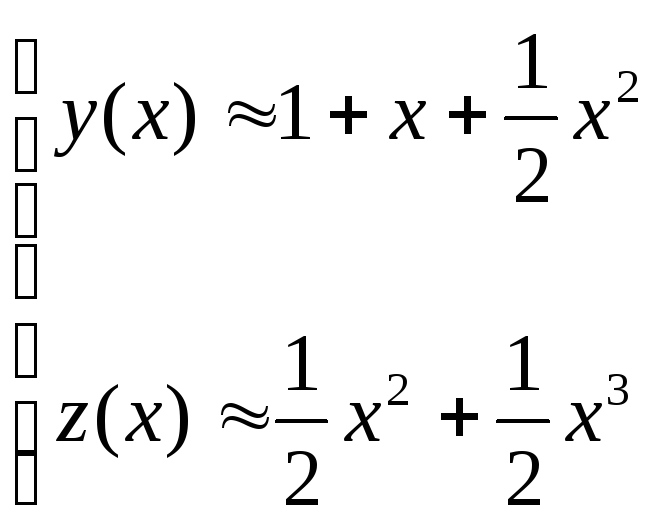
Замечание : Такой метод нахождения решения можно применять к уравнениям n-го порядка не прибегая к замене на систему ДУ первого порядка.
Пример:
Уравнение :
![]() гармонического осциллятора
гармонического осциллятора
с начальными
условиями
![]()
пусть шаг h=0.05 , на промежутке [0,3]
Записываем разложение в ряд :
![]()
Имеем :
![]()
Далее последовательно получаем :
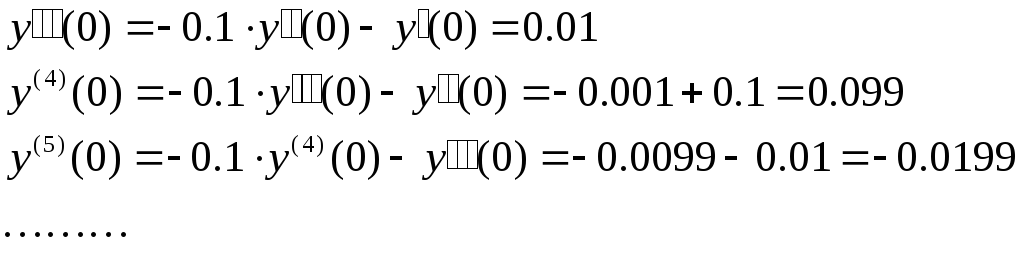
Подставив в исходное выражение , получим :
![]()
Построим график полученного решения и сравним с решением встроенной функцией


Видно , что на протяжении примерно 40 шагов имеем достаточно хорошее приближение к решению.
Метод последовательных приближений ( метод Пикара) .
Суть метода в том , что решение получают как предел последовательности функций , которые находят по рекуррентной формуле :
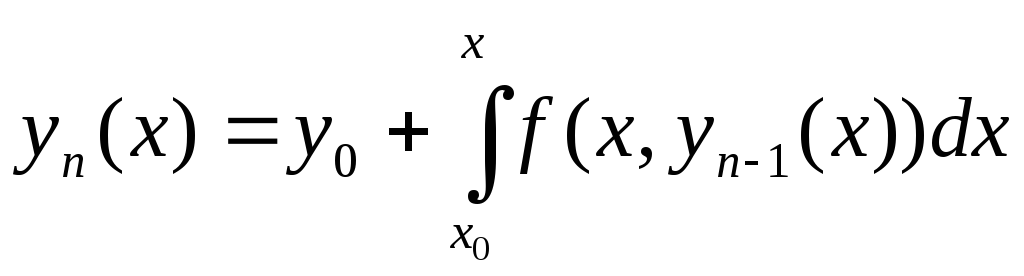
Доказано :
Если правая часть f(x,y) в некотором замкнутом прямоугольнике
R{│x-x0│≤a,│y-y0│≤b} удовлетворяет условию Липшица ( см. предыдущие лекции) , то независимо от выбора начальной функции последовательные приближения fn(x) сходятся на некотором отрезке [x0,x0+h] к решению задачи.
Оценка погрешности приближенного решения :
![]()
![]()
В качестве начального приближения y0(x)можно взять любую функцию , близкую к решению ,в том числе выгодно иногда брать функцию в виде частичной суммы степенного ряда.
Область применения метода последовательных приближений более широкая , чем метода разложения в степенной ряд. Не требуется аналитичности правой части дифференциального уравнения.
Недостаток: все более громоздкие интегралы.
Пример:
Рассмотрим Задачу Коши![]()
![]()
Заменяем на
интегральное уравнение :
![]()
В качестве начального приближения берем начальное условие.
Тогда для последовательных приближений имеем:
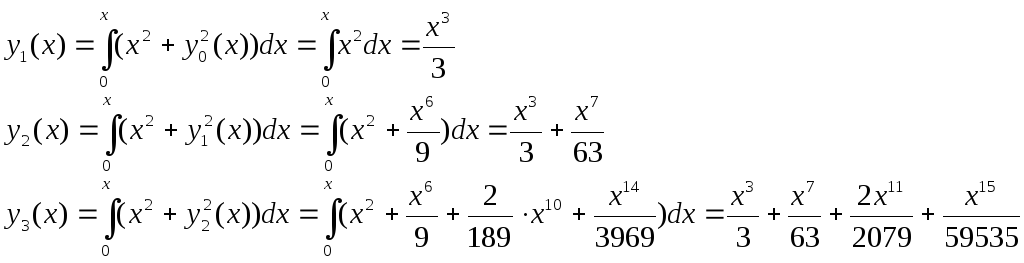
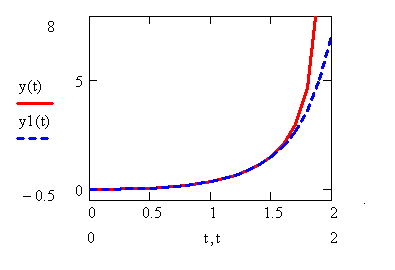
Построим график решения и сравним с встроенной функцией :
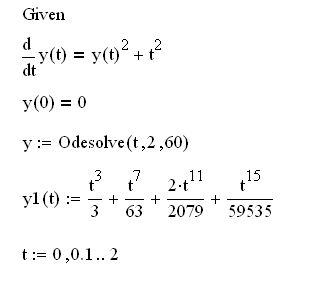
 Теперь
оценим погрешность последнего приближения
.
Теперь
оценим погрешность последнего приближения
.
Функция f(x,y)=x2+y2 определена и непрерывна на всей плоскости, значит в качестве a и b можно взять любые числа .
Пусть мы рассматриваем функцию в пределах величин , указанных на графике.
Следовательно можно вычислить :
![]()
![]()
По правилу оценки шага h=0.4
![]()
Часто такая оценка погрешности завышена .
На практике вычисления останавливают , если соседние приближения отличаются в пределах изначально заданной погрешности.
