10

Лекция 4 27.10.2006

Два дополнения к предыдущей лекции :

1. Интерполяционный полином Ньютона может быть записан в виде :

а) Для интерполяции вперед ( используются конечные разности верхних строк таблицы)

Здесь

б) Для интерполяции назад ( используются конечные разности нижних строк таблицы)

Применение полинома Ньютона имеет практические преимущества по сравнению с полиномом Лагранжа, поскольку может быть использован как в случае неравноотстоящих узлов , так и при постоянном шаге.

Пример использования полинома Ньютона рассмотрен в пособии по лабораторным работам.

2. Погрешность приближения кубическими сплайнами.

Если функция имеет на отрезке [a,b] непрерывную производную четвертого порядка , то для интерполяционного кубического сплайна справедлива оценка погрешности:

или

5.Решение числовых уравнений

5.1Постановка задачи

Математические уравнения различаются по типу искомых величин на числовые и функциональные, а по количеству искомых величин – на уравнения с одним неизвестным и системы уравнений.

Числовые уравнения – это форма связи значений одной неизвестной скалярной величины или упорядоченной группы из нескольких скалярных величин (то есть вектора) с известными величинами (параметрами уравнений). В первом случае имеем уравнение с одним неизвестным, во втором – систему из N уравнений c N неизвестными. Искомые значения называют корнями уравнений.

Для функциональных уравнений искомыми являются функции : одиночные для уравнений с одним неизвестным или упорядоченные группы (вектор-функции) для систем уравнений. Примером могут служить дифференциальные уравнения и системы таких уравнений.

Методы решения числовых и функциональных уравнений заметно различаются, хотя по ряду позиций есть аналогии.

Числовые уравнения с одним неизвестным.

Будем рассматривать уравнения алгебраические и трансцендентные.

Такие уравнения имеют вид f(x) = 0.

Будем полагать, что в конечном или бесконечном интервале [А, В] f(x) определена и непрерывна и что корни уравнения вещественны.

Всякое значение x* , обращающее функцию f(x) в нуль называется корнем уравнения или нулем функции.

Будем предполагать , что уравнение имеет изолированные корни , т.е. для каждого корня уравнения существует окрестность, не содержащая других корней этого уравнения.

Отыскание приближенных изолированных действительных корней уравнений состоит из двух этапов – отделение корней и их уточнение с заданной степенью точности.

Отделение корней представляет процедуру по разбиению всей области числовой оси на интервалы, в каждом из которых содержится один и только один корень, и ее можно выполнить двумя способами – графическим и аналитическим. При графическом методе строят график функции, который позволяет легко находить отрезки, заключающие в себе только один корень.

При аналитическом методе корни уравнения f(x)=0 можно отделить, используя следующую теорему:

Теорема 1:

Если функция f(x) непрерывна на отрезке [a,b] и принимает на концах отрезка значения разных знаков, а производная f’(x) сохраняет постоянный знак внутри отрезка, то внутри отрезка существует корень уравнения f(x)=0 и при том единственный.

Замечание : если существует непрерывная производная f’(x) и можно решить уравнение f’(x)=0 , то для отделения корней достаточно посчитать знаки самой функции f(x) в точках нулей ее производной и в граничных точках .

Пример:

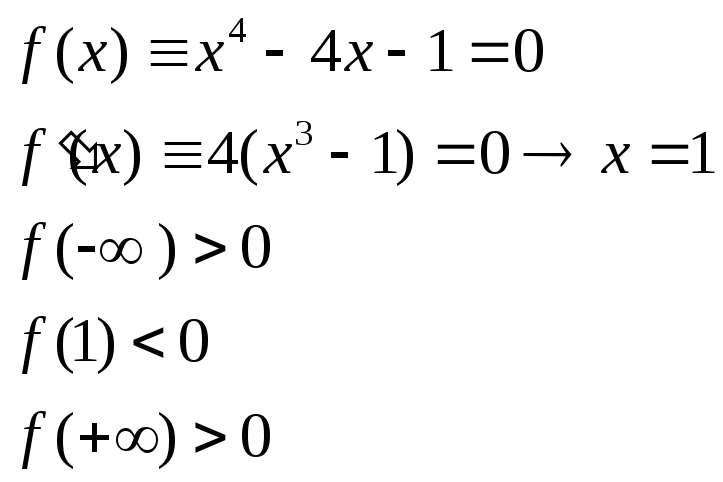
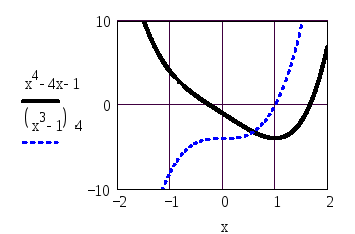
Уравнение имеет только два действительных корня в интервалах [,1[ и [1,+]

Теорема 2:

Для точного и приближенного корней уравнения f(x)=0 , находящихся на одном отрезке [,] , причем f’(x)  m >0 на этом интервале , справедлива оценка

При графическом решении уравнений часто бывает выгодно заменить исходное уравнение f(x)=0 равносильным ему уравнением (x)= (x), где новые функции более простые . тогда , построив графики этих функций , искомые корни получим как абсциссы пересечения этих графиков.

П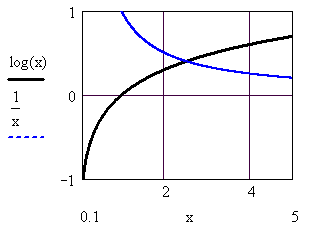ример:

Численные методы решения алг. и трансц. уравнений.