
Тема :
6. « Решение систем линейных алгебраических уравнений»
СЛУ часто встречаются в вычислительной практике как составная часть задачи. Так , например , в задачах математической физики вообще никаких уравнений кроме линейных не решаем , поскольку решение каждой сложной нелинейной задачи сводится многократному решению линейных систем.
Вообще надо сказать , что о задаче решения линейных систем как о единой задаче стоит говорить лишь когда число уравнений невелико. В этом случае это сравнительно простая задача и стандартные программы для решения линейных систем есть на всех вычислительных машинах.
Чем больше количество уравнений в системе , тем более специальную , специфическую структуру она имеет и тем более специальные свойства необходимо использовать для решения таких систем.
Некоторые виды таких систем будут рассмотрены .
-
Общие сведения и определения
Рассмотрим систему , состоящую из m ЛА уравнений с n неизвестными
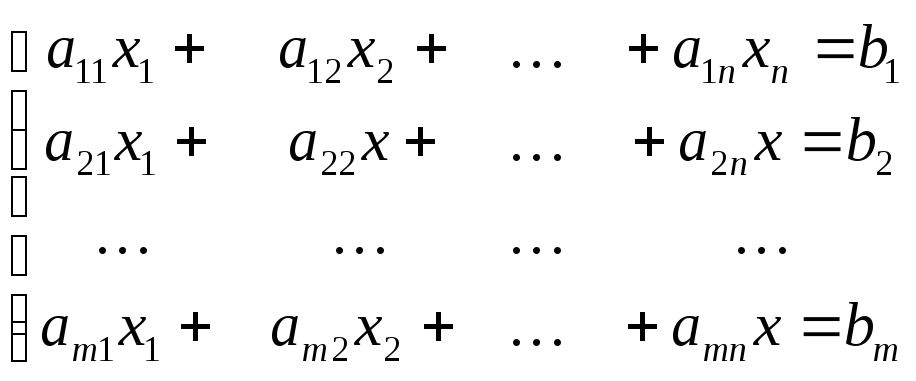 или в матричном
виде
или в матричном
виде
![]() ,
,
где А – прямоугольная матрица размерности m x n .

Определение 1.
Решением СЛАУ называется такая упорядоченная совокупность чисел
x1=c1 , x2=c2, … , xn=cn которая обращает все уравнения СЛАУ в верные равенства.
Определение 2 .
Прямыми методами решения СЛАУ называются методы , дающие решение системы за конечное число арифметических операций, которое можно по расчетной формулам оценить заранее до начала решения . Решение является точным.
При этом надо понимать, что в вычислительной математике понятие «точное решение» есть «решение с точностью до погрешности округления» , т.е. решение , которое можно было бы получить на идеализированном компьютере с бесконечной разрядностью машинного слова. В реальности погрешности округления имеются , поэтому мы говорим что «метод точный» с некоторой условностью.
Определение 3.
Итерационными методами решения СЛАУ называются методы , дающие решение системы уравнений как предел последовательных приближений – итераций , вычисляемых по единообразной схеме, начиная с некоторого начального приближения - « 0-й итерации» .
Решение является приближенным, но с любой заданной погрешностью. Требуемое количество вычислительных операций определяется в процессе счета и не может быть определено заранее.
-
Метод Гаусса
Наиболее распространенными прямыми методами решения СЛАУ являются методы исключения или методы исключения Гаусса.
Рассмотрим СЛАУ:
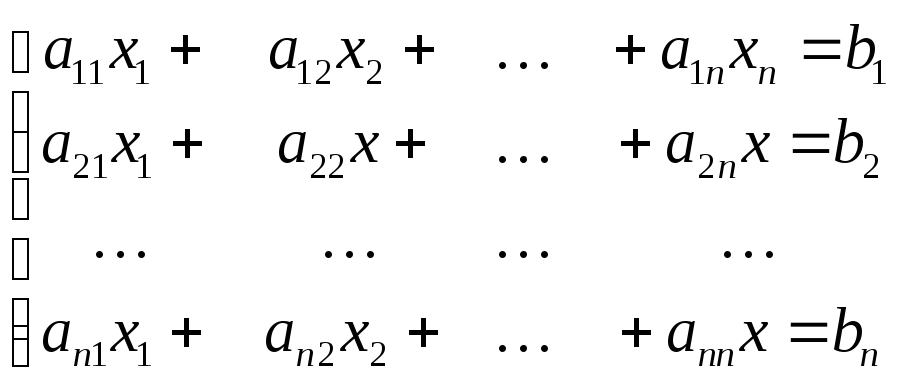 или в матричном
виде
или в матричном
виде
![]() ,
,
где А –квадратная матрица размерности n x n .
x,b – n- мерные векторы , i=1,2,…,n
Будем полагать , что матрица А невырожденная , т.е. детерминант А0 и , следовательно , решение СЛАУ существует и оно единственное.
Основная идея метода состоит в том, чтобы исходную СЛАУ
A x = b
методом исключения свести к системе вида A’ x = b’, где A’ - треугольная (например, верхняя) матрица.
Рассмотрим более подробно процесс преобразования исходной матрицы A к треугольной A’. Предполагая, что a11 0 , разделим первое уравнение СЛАУ на коэффициент a11:
![]()
Вычтем полученное уравнение из всех остальных уравнений , умножая его на соответствующий коэффициент ai1 . В результате первое неизвестное x1 окажется исключенным из всех уравнений, кроме первого, и СЛАУ примет вид:
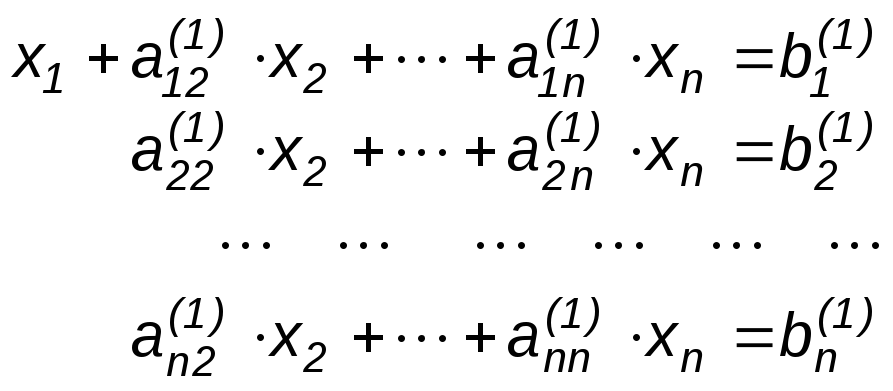
где
![]()
![]()
![]()
Далее,
предполагая, что a22
0, делим второе уравнение преобразованной
системы на коэффициент
![]() .
Затем также умножаем его на соответствующие
коэффициенты ai2
и вычитаем
из всех оставшихся уравнений преобразованной
системы , при этом из них будут исключены
неизвестные x2
, начиная
с третьего уравнения. Продолжая этот
процесс исключения неизвестных, вместо
второй системы получим эквивалентную
систему :
.
Затем также умножаем его на соответствующие
коэффициенты ai2
и вычитаем
из всех оставшихся уравнений преобразованной
системы , при этом из них будут исключены
неизвестные x2
, начиная
с третьего уравнения. Продолжая этот
процесс исключения неизвестных, вместо
второй системы получим эквивалентную
систему :
![]()
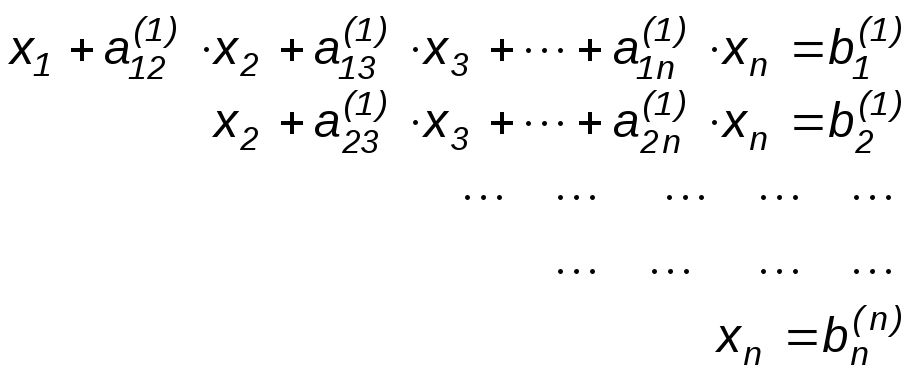
В общем случае формулы имеют вид :
а) для коэффициентов в самом верхнем уравнении на k- ом шаге исключения
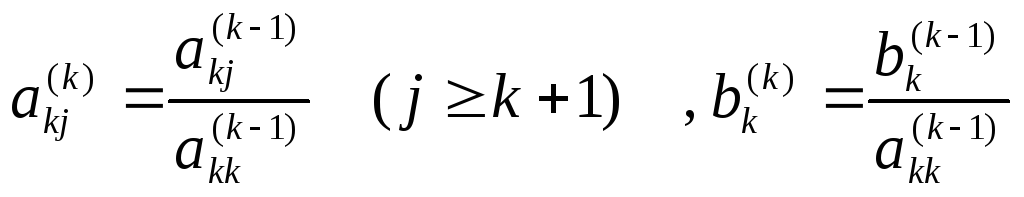
б) для остальных коэффициентов

Процесс
сведения СЛАУ к системе с треугольной
матрицей называется прямым
ходом метода
Гаусса. Выполнение указанных преобразований
возможно, если получающиеся при расчете
коэффициенты
![]() отличны от нуля. В противном случае
нужно производить перестановку уравнений,
т.к. среди коэффициентов
отличны от нуля. В противном случае
нужно производить перестановку уравнений,
т.к. среди коэффициентов
![]() обязательно найдется хотя бы один,
отличный от нуля, - иначе матрица A
была бы вырожденной.
обязательно найдется хотя бы один,
отличный от нуля, - иначе матрица A
была бы вырожденной.
В результате прямого хода СЛАУ приобретает вид:
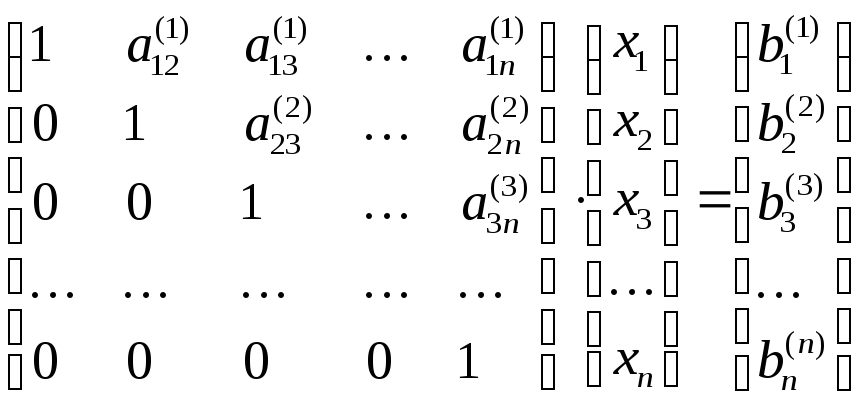
После такого преобразования алгоритм решения уже прост: из последнего уравнения легко находится xn , затем из предпоследнего xn-1 и т.д.
Этот этап решения называют обратным ходом метода Гаусса.
В результате обратного хода
![]()
Описанный алгоритм
иногда называют схемой «единственного
деления» , а элемент
![]() , на который производится деление –
ведущим элементом.
, на который производится деление –
ведущим элементом.
Если очередной ведущий элемент окажется нулевым, решений прерывается. Если очередной ведущий элемент близок к нулю – решение продолжится , но погрешности могут резко возрасти.
Погрешность
вычислений, связанную с ошибками
округления, можно уменьшить, если
выполнить перестановку уравнений в
СЛАУ таким образом, чтобы соблюдалось
условие
![]() .
.
Общее число арифметических операций S, необходимых для решения СЛАУ методом Гаусса определяется по следующей формуле
S = 2/3×n×(n+1)×(n+2) + n×(n-1),
где n - количество неизвестных.
При больших n
![]() .
.
