5.2. Модели кинематических пар с трением

Введение сил трения приводит к увеличению числа неизвестных компонент реакций кинематической пары, а количество уравнений кинетостатики при этом не возрастает. Для того, чтобы задача силового анализа осталась разрешимой, необходимо ввести дополнительные условия, количество которых равно числу неизвестных. Проще всего такие условия вводятся для высшей кинематической пары первого класса (рис.5.3). Пусть поверхности элементов пары деформируются под действием нормальной силы и касаются в малой окрестности точки А, а относительное движение звеньев определяется заданием скорости скольжения и вектора относительной угловой скорости . Направим ось z по общей нормали к поверхностям в точке А, а ось х – по линии действия вектора . Тогда все компоненты реакции выражаются через величину нормальной силы N. Используя соотношения (5.1), находим

(5.7)

где – компонента вектора угловой скорости, лежащая в плоскости хАy, а _х и _y – ее проекции на оси х и y. Формулы (5.7) выражают пять компонент реакций через шестую компоненту.

Получение аналогичных соотношений для пар с меньшей подвижностью является сложной задачей, поскольку в общем случае закон распределения нормальных реакций по поверхности или по линии соприкосновения остается неизвестным. Обычно дополнительные условия выбираются с учетом конструктивных особенностей элементов кинематической пары, позволяющих делать некоторые априорные предположения о характере распределения нормальных реакций.

Рассмотрим некоторые примеры формирования таких условий, т.е., по существу, примеры построения расчетных динамических моделей кинематических пар с трением.

а) Поступательная пара в плоском механизме. Пусть при силовом расчете плоского механизма ставится задача определения реакций, лежащих в плоскости движения. При этом в идеальной поступательной паре неизвестными компонентами реакций будут (рис.5.4) сила R_y, перпендикулярная линии движения ползуна, и момент ; при наличии трения возникает еще одна компонента R_x.

а) б)

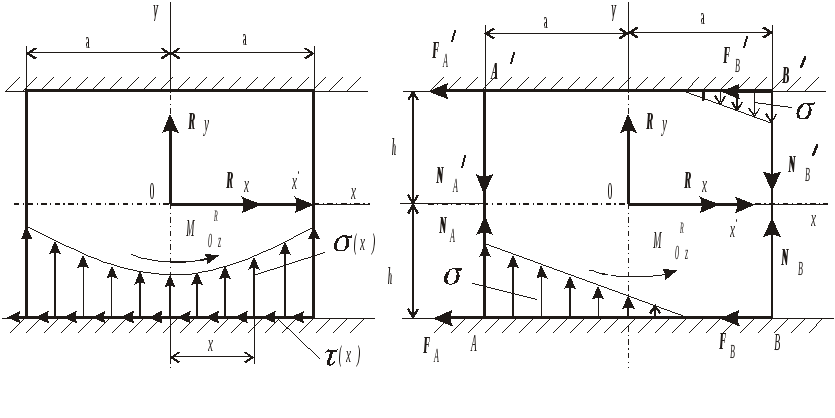
Рис. 5.4

Чтобы задача силового расчета оставалась разрешимой, эту третью компоненту необходимо выразить через первые две или выразить все три неизвестные составляющие через какие-либо два параметра. Сделать это можно различными способами, основываясь на разных предположениях относительно характера распределения нормальных сил по поверхностям соприкосновения. Предположим сначала, что эти силы распределяются некоторым образом по одной из двух контактных плоскостей, например, по нижней (рис.5.4, а). Если (х) – нормальная сила, приходящаяся на единицу длины линии контакта в точке с координатой х, то удельная сила трения , возникающая в той же точке, определяется из выражений (5.1) и (5.2):

(5.8)

Здесь функция (знак ) означает, что силы трения, действующие на ползун, направлены противоположно его скорости. Из (5.8) получаем

(5.9)

поскольку в данном случае

Таким образом, мы получили выражение, связывающее реакцию R_x с R_y и тем самым сводящее число неизвестных компонент реакций к двум. Отметим, что при соприкосновении ползуна и направляющей по верхней плоскости знак R_y изменится на противоположный, а знак R_x в силу (5.9) сохранится. В дальнейшем выражение (5.9) нам будет удобно представить в форме

(5.10)

с учетом того, что

Предположение о том, что контакты ползуна с направляющей происходят только по одной из плоскостей, не всегда оказывается приемлемым. Часто становится необходимым учитывать перекос ползуна, при котором контакт возникает на обеих плоскостях (рис.5.4, б). При этом и выражение (5.9) становится неверным.

В этом случае можно воспользоваться другой моделью поступательной пары. Примем условно, что нормальные силы, возникающие на поверхностях контакта, могут быть заменены двумя сосредоточенными силами N_A и N_B, приложенными в крайних точках ползуна. В зависимости от распределения нормальных сил (х) силы N_A и N_B могут быть приложены в точках А и B , либо в точках А’ и B’ и направлены соответственно либо вверх, либо вниз. Выразим теперь все три компоненты реакций кинематической пары через два параметра – N_A и N_B. Из рис.5.4, б получаем

(5.11)

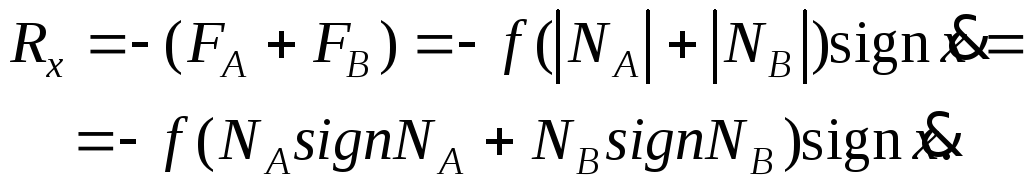(5.12)

Учитывая, что при переходе точки контакта с одной плоскости на другую направление силы трения не изменяется, а направление момента этой силы относительно точки 0 изменяется на противоположное, получаем

(5.13)

Отметим, что при отсутствии трения (f = 0) реакции N_A и N_B будут иметь разные знаки, если Это условие, вообще говоря, может рассматриваться как критерий, указывающий на необходимость использования модели, описываемой уравнениями (5.11)-(5.13).

Для более удобного запоминания сведем модели поступательных пар в табл. 5.1.

Таблица 5.1

	Без трения	Одноточечный контакт	Двухточечный контакт
Rx	0
Ry	Ry	Ry	NA + NB

б) Вращательная пара в плоском механизме. На рис.5.5 представлены динамические модели вращательных пар с трением при учете только компонент реакций, лежащих в плоскости, перпендикулярной оси шарнира.

a) б)

Рис. 5.5

В модели, показанной на рис.5.5, a, предполагается, что силы нормального взаимодействия сосредоточены в точке А, и в этой же точке приложена сила трения F. Проецируя силы трения на оси координат и определяя их моменты, находим

(5.14)

Здесь  – угол между линией действия силы N и осью х, r – радиус цапфы. В формулах (5.14) учтено, что с изменением знака N меняется направление силы F, поскольку точка ее приложения из А смещается в А₁.

В выражение для момента введен множитель , показывающий, что момент сил трения, возникающих во вращательной паре, направлен противоположно относительной угловой скорости. Это выражение показывает также, что линия действия равнодействующей сил реакций во вращательной паре является касательной к окружности с радиусом и центром в точке О.

В модели, показанной на рис.5.5, б, предполагается, что нормальные силы () распределены по полуокружности симметрично относительно точки А. Обычно закон распределения выбирается в форме Силы трения также являются распределенными; при этом .

Проецируя силы на направление радиуса АО и перпендикулярное к нему, а также определяя момент сил относительно точки О, находим

Отсюда получаем

(5.15)

Сравнивая эти выражения с (5.14), замечаем, что они отличаются только увеличением момента сил трения в 4/ раз. Первая модель обычно используется при расчете кинематических пар со значительными зазорами (например, изношенных).

Сведем модели вращательных пар в табл. 5.2.

Таблица 5.2

	Без трения	Пара с зазором (изношенная)	Приработавшаяся цапфа
Rx	Rx	Ncosα – fNsinα	Ncosα – fNsinα
Ry	Ry	Nsinα + fNcosα	Nsinα + fNcosα
	0

в) Червячное зацепление. На рис.5.6, а представлен фрагмент червяка.

Предполагается, что рабочие поверхности витка червяка и зуба червячного колеса контактируют в точке В (или В’), т.е. условно принято, что в зацеплении образуется пятиподвижная кинематическая пара. В точке контакта возникают нормальная сила (или ) и сила трения (или ), касательная к поверхности витка червяка и направленная противоположно скорости скольжения. Для дальнейших расчетов удобно найти проекции этих сил на направления, параллельные осям червяка и червячного колеса. Введем систему координат Bxyz, где ось Bx параллельна оси червячного колеса, ось Вy – оси червяка, а ось Bz параллельна линии межосевого расстояния (рис.5.6, б). Если повернуть систему координат Bxyz вокруг оси Bz на угол β, то есть до совмещения оси Вх с линией действия силы трения , то получим систему координат Bx^*y^*z^*. В этом случае ось Bx^* будет направлена по касательной к поверхности витка червяка в точке контакта В. Угол β – угол подъема винтовой линии червяка (при β = 0 винтовая линия обращается в кольцевую). Далее повернем новую систему координат Вx^*y^*z^* вокруг оси Bx^* на угол α до совмещения оси Вy^* с линией действия нормальной силы N. Получим новую систему координат Вx^**y^**z^**, в которой ось Вy^** направлена перпендикулярно поверхности червяка в точке контакта В. Угол α – угол профиля исходного контура (при α=0 виток червяка становится прямобочным). Тогда несложно получить проекции сил и на оси системы координат Вxyz (рис.5.7):

S = Nּcosαּcosβ – Fּsinβ =N(cosαּcosβ – fּ signNּsinβּsign),

P = Nּcosαּsinβ + Fּcosβ =N(cosαּsinβ + fּsignNּcosβּsign), (5.16)

T = Nּsinα.

Здесь S – осевая сила на червяке (окружная сила на червячном колесе); P – окружная сила на червяке (осевая на червячном колесе); Т – радиальная сила.

152