Экзамен / тмм - экзамен(и задачи) / ТММ / tmm_11

4.3. Решение уравнений кинетостатики

Для механизмов с идеальными связями уравнения кинетостатики представляют собой систему линейных алгебраических уравнений, обладающую единственным решением, если избыточные связи в системе отсутствуют, а рассматриваемое положение механизма не является особым. Для сложных механизмов, содержащих большое число подвижных звеньев, система уравнений кинетостатики имеет высокий порядок (для N–1 подвижных звеньев – 6ּ(N–1) уравнений). Ее решение существенно облегчается тем, что она может быть разделена на несколько независимых систем, каждая из которых содержит обобщенную движущую силу и реакции кинематических пар, действующие на звенья одной структурной группы. Действительно, для каждой структурной группы, не содержащей избыточных связей, справедлива структурная формула

(4.23)

где w_G – число степеней подвижности группы, N_G – число подвижных звеньев группы, p_SG – число s-подвижных кинематических пар в группе. С другой стороны, как было показано выше, сумма

(4.24)

представляет собой число неизвестных движущих сил и реакций в идеальных связях, подлежащих определению. Сравнивая выражения (4.23) и (4.24), замечаем, что n_u=6N_G, т.е. число неизвестных сил равно числу уравнений кинетостатики. Таким образом, уравнения кинетостатики могут решаться последовательно для каждой структурной группы.

Силовой расчет следует производить в направлении, обратном геометрическому и кинематическому расчетам, т.е. начинать его с групп последнего слоя. Тогда реакции во внешних кинематических парах групп m–го слоя оказываются известными и могут рассматриваться как заданные силы при расчете групп (m–1)-го слоя.

Особенности расчета плоского механизма. В плоском механизме, выделяя последовательно плоские структурные группы, можно для каждой из них определить отдельно компоненты реакций, лежащих в плоскости движения х0y (R_x, R_y, ), и обобщенные движущие силы. Компоненты реакций, не лежащие в плоскости движения, входят в другую группу уравнений. Часто из-за наличия избыточных связей определение всех реакций второй группы (Rz, , ) становится невозможным; в этом случае приходится ограничиваться определением только реакций освобождающих связей.

Рассмотрим некоторые примеры.

а) На рис.4.4 показан плоский механизм с одной степенью подвижности, состоящий из двух структурных групп: однозвенной одноподвижной группы (звено 1) и группы Ассура типа ВВП (звенья 2 и 3).

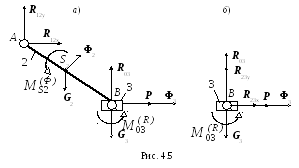
На рисунке нанесены активные силы: заданные и подлежащие определению (движущий момент Q), а также силы инерции, лежащие в плоскости движения , и проекции моментов сил инерции на ось z, перпендикулярную плоскости движения (). Силовой расчет начинается с последней группы, т.е. группы Ассура ВВП (рис.4.5, а). В соответствии с принципом освобождаемости от связей в шарнире А и в ползуне В приложены реакции отброшенных связей. На рисунке показаны компоненты реакций, лежащие в плоскости движения. Во вращательных парах (например, в шарнире А) возникают реакции с компонентами R_x и R_y, а в поступательных парах (например, в поступательной паре В) – нормальная реакция R и момент . Каждая компонента реакций снабжена двумя индексами, указывающими номер воздействующего звена и номер звена, воспринимающего воздействие. Следовательно, в шарнире А со стороны звена 1 на звено 2 действуют компоненты реакции R_12x и R_12y, а в поступательной паре В со стороны стойки 0 на ползун 3 действуют реакция R₀₃ и момент .

Реакция в шарнире В является внутренней для группы, поэтому она на рисунке не показана. Для того, чтобы включить в рассмотрение реакцию в шарнире В, надо отбросить либо звено 2, либо звено 3. На рис.4.5, б оставлено звено 3 (ползун); к указанным ранее силам добавлены компоненты реакции R_23x и R_23y, действующей со стороны звена 2 на звено 3.

Таким образом, в группе ВВП в плоскости, перпендикулярной оси z, всего 6 неизвестных: R_12x, R_12y, R_23x, R_23y, R₀₃, . Для плоской двухзвенной группы можно составить 6 независимых уравнений кинетостатики. В некоторых случаях удается так составить уравнения, чтобы в них было по одному неизвестному. Например, для звена 3 из условия равенства нулю суммы моментов всех сил относительно оси Bz (т.е. оси z, проходящей через точку B) следует: .

Сумма моментов всех сил, действующих на звенья 2 и 3, относительно оси Аz:

(Р + Ф₃)(y_A – y_B) – (R₀₃ – G₃)(x_A – x_B) + Ф_2x(y_A – y_S2) –

– (Ф_2y – G₂)(x_A – x_S2) + = 0,

где Ф_2х и Ф_2y – проекции главного вектора сил инерции второго звена, х_А, y_A, x_B, y_B, x_S2, y_S2 – координаты точек соответственно А, В, S₂. Отсюда можно найти реакцию R₀₃. После этого легко определяются остальные неизвестные. Уравнения для ползуна 3:

R_23x + P + Ф₃ = 0,

R₀₃ + R_23y – G₃ = 0.

Уравнения для звеньев 2 и 3:

R_12x + Ф_2x + P + Ф₃ = 0;

R_12y + Ф_2y – G₂ + R₀₃ – G₃ = 0.

После определения всех реакций в группе ВВП переходят к расчету первой структурной группы (рис.4.6).

Реакции в шарнире А уже известны: в соответствии с третьим законом Ньютона R_12x=–R_21x, R_12y=–R_21y. Следовательно, остаются три неизвестные: компоненты реакции R_01x, R_01y в шарнире 0 и движущий момент Q. Для кривошипа можно составить три уравнения кинетостатики, из которых находятся оставшиеся неизвестные. Если угловая скорость вращения кривошипа постоянна и центр масс находится на оси вращения О, то уравнения кинетостатики можно записать в виде:

R_21x + R_01x = 0,

R_21y + R_01y – G₁ = 0,

R_21x(y₀ – y_A) – R_21y(x₀ – x_A) + Q = 0.

П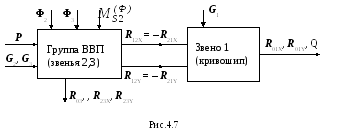оследовательность силового расчета проиллюстрирована на схеме рис.4.7. Предварительно определяются силы инерции . Потом решаются 6 уравнений для звеньев 2 и 3 группы ВВП, входящей во второй слой, находятся реакции R_12x, R_12y, R_23x, R_23y, R₀₃, . Затем решаются три уравнения для звена 1, являющегося группой первого слоя. Реакции R_21x и R_21y рассматриваются как известные (R_12x = – R_21x, R_12y = – R_21y). Определяются реакции R_01x, R_01y и движущий момент Q.

б) Механизм с тремя степенями подвижности (рис.4.8). Данный механизм состоит из трех одноподвижных групп: двух однозвенных (звенья 1 и 5) и одной трехзвенной (звенья 2, 3, 4). Определив силы инерции и моменты сил инерции звеньев, а также задав значения активных сил P_3X и P_3Y, приложенных в точке С₃ звена 3, и момента М^w, приступаем к силовому расчету последней структурной группы АВСD. Для плоской системы сил, действующих на три звена этой группы, составляем 9 уравнений кинетостатики, из которых определяем обобщенную движущую силу Q₂ и 8 реакций (R_12X, R_12Y, R_23X, R_23Y, R_34X, R_34Y, R_54X, R_54Y). Затем приступаем к расчету однозвенных групп первого слоя ОА и ЕD. При этом силы R_21X = – R_12X, R_21Y = – R_12Y, R_45X = – R_54X, R_45Y = – R_54Y рассматриваются уже как известные, найденные на предыдущем этапе. Из уравнений кинетостатики для звена ОА определяем R_01X, R_01Y и обобщенную движущую силу Q₁; из уравнений, составленных для звена ЕD, определяем R_05X, R_05Y и обобщенную движущую силу Q₃.

Н а рис.4.9 схематично представлен алгоритм силового расчета этого механизма. Для каждой группы указаны заданные («входные») силы и силы, найденные при силовом расчете.

Рис. 4.9

Силовой расчет по кинетостатической модели может производиться не только решением уравнений кинетостатики, составленных для каждого звена в отдельности, но и с помощью других методов. Рассмотрим, каким образом можно провести расчет трехзвенной группы АВСD, показанной на рис.4.8, методом размыкания кинематической цепи. Разомкнем кинематическую цепь в шарнире D и введем реакции освобождающих связей R_54X и R_54Y. Составим уравнения равновесия моментов всех активных сил, всех сил инерции и введенных реакций связей относительно осей шарниров А, В, С. Получим три уравнения:

Из этих уравнений определяются три неизвестные величины: R_54X, R_54Y и Q₂. После этого определение реакций в шарнирах А, В, С не вызывает затруднений; их можно найти, например, из уравнений проекций на оси х и y сил, действующих на звенья 2, 3, 4.

Решение уравнений кинетостатики усложняется, если в механизме имеются избыточные связи. В этом случае система становится статически неопределимой, поскольку число неизвестных реакций и движущих сил превосходит число уравнений кинетостатики. В ряде случаев удается избежать статической неопределимости увеличением подвижности некоторых кинематических пар (например, заменой вращательных пар цилиндрическими или сферическими); однако этот путь, связанный с изменением конструкции механизма, часто оказывается нежелательным как из-за снижения жесткости механической системы, так и по технологическим соображениям. В отдельных случаях оказывается возможным условно в расчетной схеме увеличить подвижность кинематических пар, учитывая некоторые свойства реальной конструкции. Так, например, наличие зазоров во вращательной паре (между осью шарнира и его втулкой) позволяет рассматривать при расчете эту пару как сферическую, считая равными нулю моменты, возникающие в ней при угловых перекосах. Однако в общем случае провести полный силовой расчет механизма с избыточными связями можно только за счет отказа от динамической модели жесткого механизма и введения расчетной схемы, учитывающей упругость звеньев и их соединений. Рассмотрение такой усложненной модели выходит за рамки дисциплины ТММ.

Вместе с тем всегда имеется возможность выполнить частичный силовой расчет механизма, ограничиваясь определением обобщенных движущих сил и реакций всех освобождающих связей. (Напомним, что освобождающей мы называем такую связь, устранение которой приводит к увеличению числа степеней подвижности механизма на единицу). Такой ограниченный расчет можно выполнить разными методами; один из них основан на использовании общего уравнения динамики.

4.4. Применение общего уравнения динамики

для силового расчета механизмов

Для любой системы материальных точек с идеальными связями сумма работ всех активных сил и всех сил инерции на любом возможном перемещении в любой фиксированный момент времени равна нулю. Это положение записывается в аналитической форме:

(4.25)

и называется уравнением Даламбера-Лагранжа или общим уравнением динамики. В уравнении (4.25) и – активная сила и сила инерции к-й материальной точки, – ее возможное перемещение, т.е. любое бесконечно малое перемещение, совместимое с наложенными на систему связями в данный фиксированный момент времени (в отличие от действительного малого перемещения, соответствующего бесконечно малому приращению времени t); М – число материальных точек в системе.

Р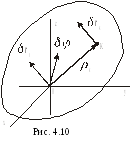ассмотрим звено механизма, являющееся абсолютно твердым телом. Введем систему координат 0хyz, связанную с этим телом (рис.4.10). Для произвольной точки звена имеем

, (4.26)

где – возможное перемещение полюса 0, – вектор бесконечно малого поворота, – радиус-вектор к-й точки. Подставив (4.26) в (4.25), находим

(4.27)

Здесь и – главные векторы, а и – главные моменты активных сил и сил инерции звенa. Складывая выражения (4.27) для всех подвижных звеньев, приводим уравнение (4.25) для механизма с жесткими звеньями и идеальными кинематическими парами к следующей форме

(4.28)

где N – число подвижных звеньев. Необходимо отметить, что каждое из выражений (4.27) в отдельности нулю не равно, поскольку не равна нулю работа сил реакций, действующих на каждое отдельное звено.

Если механизм имеет w степеней свободы и q₁,…,q_w – его обобщенные координаты, то

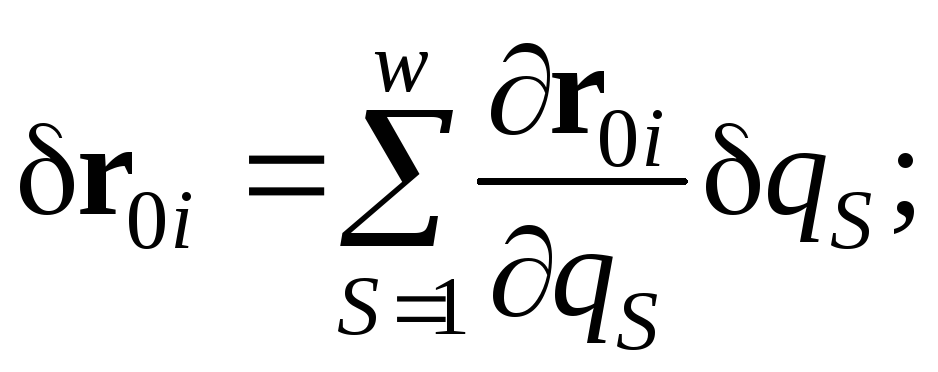
(4.29)

Подставляя (4.29) в (4.28) и используя независимость вариаций обобщенных координат q_S, получаем следующую систему уравнений:

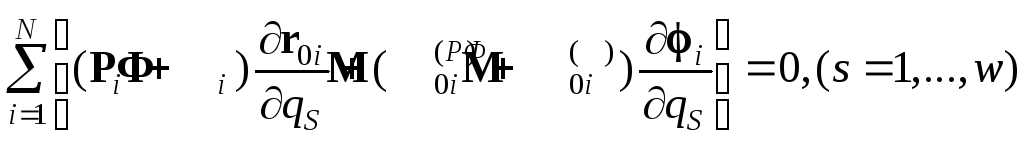. (4.30)

Отметим, что выражение следует понимать не как частную производную от функции положения _i (q₁, …, q_w ), поскольку вектор угла поворота в общем случае вообще не существует как функция положения, а как отношение бесконечно малого угла поворота к бесконечно малому парциальному возможному перемещению q_S. Выражение может рассматриваться также как отношение парциальной угловой скорости к скорости при = 0 для всех ks. Производная является обычной частной производной от функции положения r_0i( q₁, …, q_w) по координате q_S.

Для механизма с одной степенью подвижности система (4.30) сводится к одному уравнению

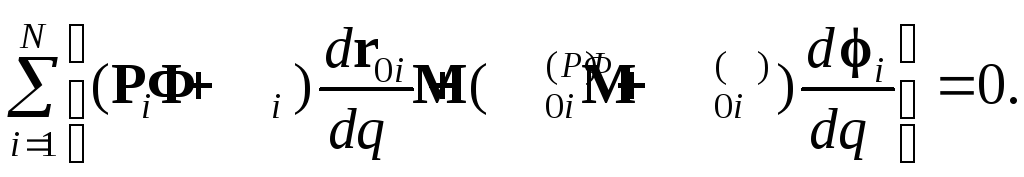(4.31)

Поскольку в этом случае , где – скорость точки 0_i, уравнение (4.31) записывается также в форме

(4.32)

Отсюда следует, что сумма возможных мощностей всех активных сил и сил инерции в любой момент времени равна нулю для механизма с одной степенью подвижности при идеальных кинематических парах.

Уравнение Даламбера-Лагранжа в форме (4.28) удобно использовать для определения обобщенных движущих сил. Учитывая, что работа движущей силы Q_S на возможном перемещении q_S равна Q_Sq_S , и выделяя обобщенные движущие силы из прочих активных сил, имеем

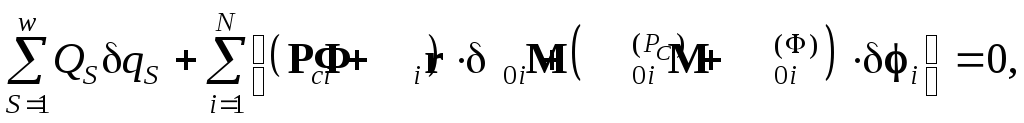(4.33)

где – главный вектор всех активных сил, приложенных к i–му звену, кроме движущих, а – главный момент этих сил. Из (4.33) получаем уравнения, аналогичные (4.30):

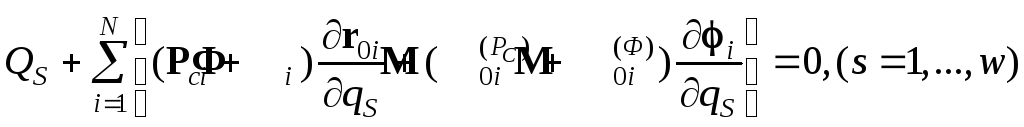. (4.34)

Эти уравнения могут быть непосредственно использованы для определения обобщенных движущих сил Q_S. Отметим, что они остаются в силе и для механизмов с любым числом избыточных идеальных связей. Для механизма с одной степенью подвижности из (4.31) находим:

(4.35)

Рассмотрим в качестве примера задачу об определении движущей силы для рычажного механизма, показанного на рис.4.4. Поскольку в плоском механизме векторы возможных перемещений всех точек параллельны плоскости движения, а векторы малых поворотов звеньев перпендикулярны ей, для составления уравнений Даламбера-Лагранжа достаточно определить компоненты активных сил и сил инерции, лежащие в плоскости движения, и компоненты моментов, ей перпендикулярные. Остальные компоненты сил и моментов не совершают работы на возможном перемещении плоского механизма, а следовательно, и не влияют на величины движущих сил.

Уравнение Даламбера-Лагранжа для механизма, показанного на рис.4.4, составляем в форме (4.35); получаем

(4.36)

где ₂ – абсолютный угол поворота звена 2.

Общее уравнение динамики позволяет определить реакции всех освобождающих связей. Пусть, например, для механизма, показанного на рис.4.4, требуется определить реакцию R₀₃ в поступательной паре. Освободим связь, соответствующую этой реакции; для этого введем условную дополнительную степень подвижности, предположив, что направляющая ползуна может перемещаться в направлении оси y (рис.4.11). Тогда получим механизм с двумя степенями подвижности, в котором координата y_B будет играть роль второй входной координаты, а реакция R₀₃ станет обобщенной «движущей» силой, соответствующей этой координате.

Применим к этому механизму общее уравнение динамики в форме (4.34); для силы R₀₃ получим следующее выражение:

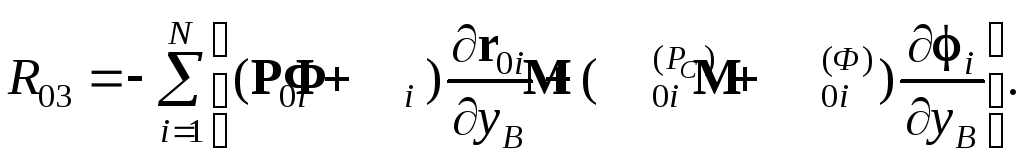(4.37)

Отметим, что силы и моменты сил инерции, входящие в это выражение, должны определяться при заданных значениях и при y_B = 0, = 0, =0, т.е. они должны вычисляться для заданного движения исследуемого механизма без какого-либо учета дополнительной подвижности. Выражение (4.37) получено из условия равенства нулю работ активных сил и сил инерции на возможном перемещении, соответствующем q = 0, y_B  0. Легко видеть, что при таком перемещении работу будут совершать только силы, приложенные к звеньям 2 и 3. При этом из уравнения (4.37) получим

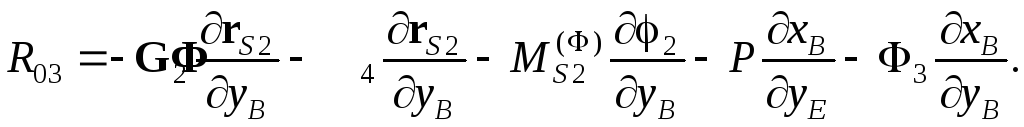(4.38)

Из геометрических соображений (см. рис.4.11) можно получить, что

(4.39)

Подставив (4.39) в (4.38), находим величину R₀₃ в заданном положении. Изложенный метод можно применить для определения реакции любой освобождающей связи. Что же касается неосвобождающих связей, то соответствующие им реакции в принципе невозможно определить в процессе силового расчета механизма.

139