Содержание

Предисловие 4

1 Уравнения первого порядка, разрешенные относительно производной 5

1.1 Уравнения с разделяющимися переменными и приводящиеся к ним 5

1.2 Однородные уравнения и приводящиеся к ним 12

1.3 Линейные уравнения 1-го порядка. Уравнения Бернулли 20

1.4 Уравнение в полных дифференциалах. Интегрирующий множитель 27

1.5 Дифференциальные уравнения 1-го порядка, не разрешенные относительно производной 43

2 Дифференциальные уравнения высших порядков, допускающие понижение порядка 56

3 Линейные дифференциальные уравнения n-го порядка 71

3.1 Линейные однородные уравнения с постоянными коэффициентами 71

3.2 Линейные неоднородные уравнения с постоянными коэффициентами 82

3.3 Уравнения Эйлера 94

4 Системы линейных дифференциальных уравнений с постоянными коэффициентами 99

5 Линейные и квазилинейные дифференциальные уравнения в частных производных первого порядка 123

1 Уравнения первого порядка, разрешенные относительно производной

1.1 Уравнения с разделяющимися

переменными и приводящиеся к ним

Дифференциальное уравнение

(1.1)

где коэффициент при зависит только от , а коэффициент при - только от , называется уравнением с разделенными переменными.

Общим интегралом такого уравнения в предположении, что обе функции и непрерывны, будет

(1.2)

или

(1.3)

Особых решений нет.

Дифференциальное уравнение

(1.4)

называется уравнением с разделяющимися переменными. Умножая обе части уравнения (1.4) на , получаем уравнение с разделенными переменными:

(1.5)

Общим интегралом этого уравнения, а следовательно, и уравнения (1.4) будет в предположении, что все функции непрерывны,

(1.6)

или

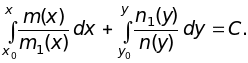(1.7)

Замечание Деление на может привести к потере частных решений, обращающих в нуль произведение . Эти решения, и только они, могут оказаться особыми.

Дифференциальное уравнение вида

(1.8)

где - постоянные, заменой переменных

(1.9)

преобразуется в уравнение с разделяющимися переменными.

Пример Найти общий интеграл уравнения

Решение. Разделяем в уравнении переменные и интегрируем:

Далее из уравнения находим решения уравнения: . Первое из этих решений частное, второе - особое.

Задание 1.1 Проинтегрировать уравнение.

1

Ответ:

2

Ответ:

3

Ответ:

4

Ответ:

5

Ответ:

6

Ответ:

7

Ответ:

8

Ответ:

9

Ответ:

10

Ответ:

11

Ответ:

12

Ответ:

13

Ответ:

14

Ответ:

15

Ответ:

16

Ответ:

17

Ответ:

18

Ответ:

19

Ответ:

20

Ответ:

21

Ответ:

22

Ответ:

23

Ответ:

24

Ответ:

25

Ответ:

26

Ответ:

27 (подстановка ).

Ответ:

28

Ответ:

29

Ответ:

30

(подстановка ).

Ответ: