Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет им. М.В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

R5.DOC

Скачиваний:

Добавлен:

18.07.2019

Размер:

578.56 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Решение. Выпишем систему для определения и :

Характеристическое уравнение

имеет корни

Подставляя в , получим два уравнения для определения и :

из котоых одно является следствием другого (в силу того, что определитель системы равен нулю). Мы можем взять тогда первое частное решение выпишется так

Аналогично, подставляя в корень найдем второе частное решение:

Перейдем к новой фундаментальной системе решений:

Пользуясь известной формулой Эйлера

где - действительное число, получим

Общим решением системы будет:

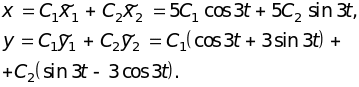
3 Случай кратных корней.

Пример Решить систему

Решение. Характеристическое уравнение

или имеет кратный корень

Решение следует искать в виде

Подставляя в первое уравнение системы, получим:

Сравнивая коэффициенты при одинаковых степенях в левой и правой части , получим:

откуда

Величины и остаются произвольными. Обозначая их соответственно через и , получим общее решение системы в виде:

Замечание Легко проверить, что если подставить во второе уравнение системы, то получим тот же результат.

4.3 Решение системы дифференциальных

уравнений нахождением интегрируемых

комбинаций (метод Д’Аламбера)

Этот метод интегрирования системы дифференциальных уравнений (не обязательно линейных) состоит в следующем: посредством подходящих арифметических операций (например, сложения, вычитания и др.) из уравнений заданной системы образуют так называемые интегрируемые комбинации, т.е. достаточно просто интегрируемые уравнения вида

(4.11)

где – некоторая функция от искомых функций

Пример Решить систему

Решение. Перепишем исходную систему в виде

Сложив почленно, получим

или

откуда

Потенцируя, будем иметь

Вычитая почленно из первого уравнения второе, получим

или

отсюда

Разрешая и относительно и , найдем общее решение системы:

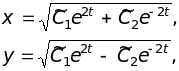
где

4.4 Метод вариации постоянных

Проиллюстрируем этот способ на примере трех неоднородных уравнений.

Пусть задана система

(4.12)

Мы предполагаем, что общее решение соответствующей однородной системы уже найдено.

Пусть оно имеет вид:

(4.13)

Будем искать решение неоднородной системы (4.12) в виде

(4.14)

где - новые неизвестные функции. Подставим (4.14) в (4.12), тогда первое уравнение (4.12) примет вид

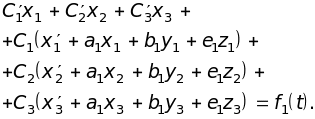(4.15)

Все суммы, стоящие в скобках, обратятся в нуль (в силу (4.13)), так что будем иметь

(4.16)

Аналогично из второго и третьего уравнений (4.12) после подстановки в них (4.14) получим

(4.17)

Система уравнений (4.16), (4.17), линейных относительно имеет решение, так как ее определитель

(4.18)

в силу линейной независимости частных решений соответствующей однородной системы. После нахождения с помощью интегрирования найдутся и а тем самым будет найдено и решение (4.14) неоднородной системы (4.12).

Пример Методом вариации постоянных решить систему

Решение. Сначала решим однородную систему

Дифференцируем первое уравнение по

Но из второго уравнения поэтому получим

Из первого уравнения так что

или

Общее решение этого уравнения есть

Так как

то получим

Заменив на будем иметь

Это и есть общее решение однородной системы.

Ищем теперь решение неоднородной системы в виде

После подстановки в исходную систему получим

Откуда

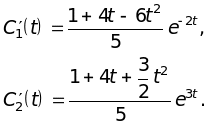
Следовательно,

где - постоянные интегрирования.

Подставляя найденные значения в , получим общее решение исходной системы:

Задание 4 Проинтегрировать линейную неоднородную систему, применяя следующие методы:

а) общее решение соответствующей однородной системы найти путем сведения системы к одному уравнению;

б) общее решение соответствующей однородной системы найти методом Эйлера;

в) используя найденное общее решение соответствующей однородной системы, найти общее решение неоднородной системы методом вариации произвольных постоянных.