
Коллоквиум / A / Вариант 01
.docТест по векторной алгебре и аналитической геометрии
для студентов I курса ММФ преподаватель – доц. Лагунова М. В.
ВАРИАНТ №0
0. Дайте определение векторного произведения.
Даны
точки
![]() ,
найдите
,
найдите
-
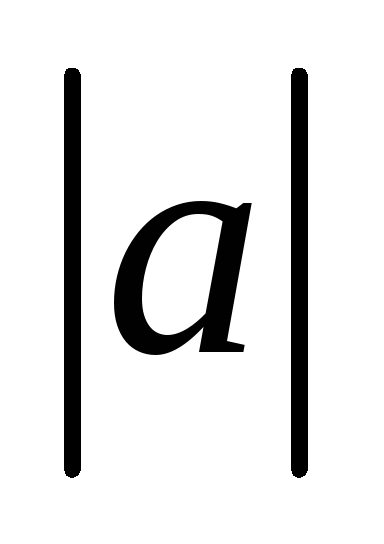 ,
, -
аппликату вектора
 ;
; -
проекцию вектора
 на ось абсцисс;
на ось абсцисс; -
косинус угла между направлениями вектора
 и оси ординат.
и оси ординат.
Даны
векторы
![]() найдите
найдите
-
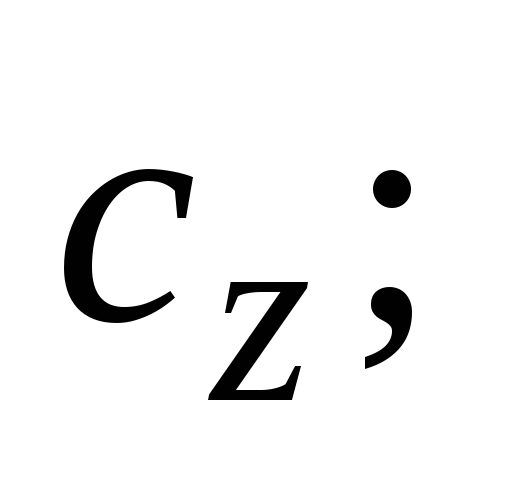
-
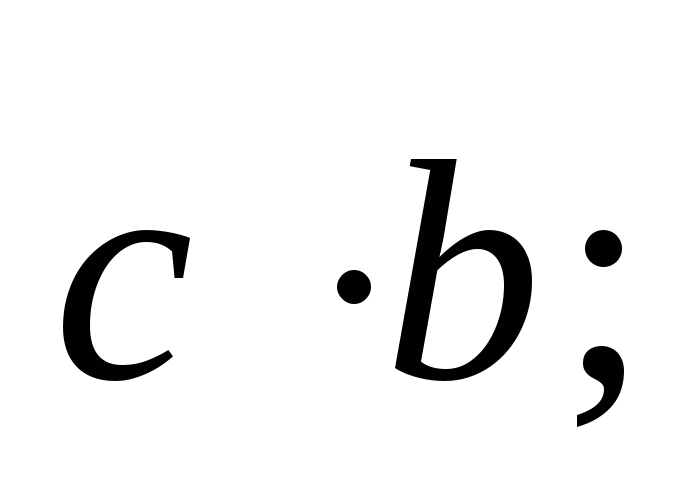
-
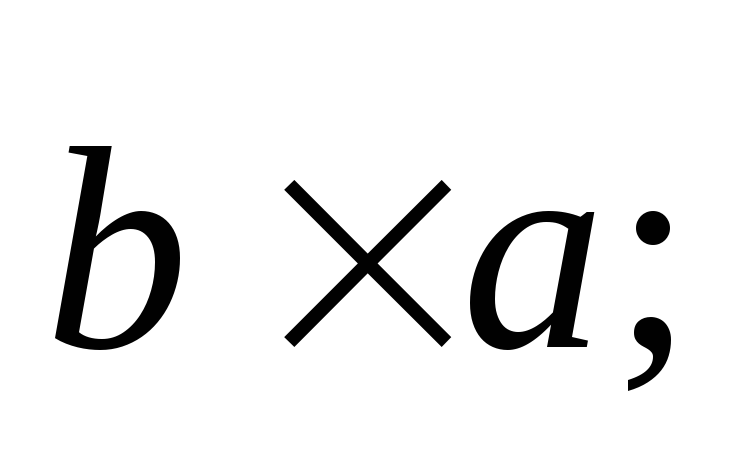
-
Точка
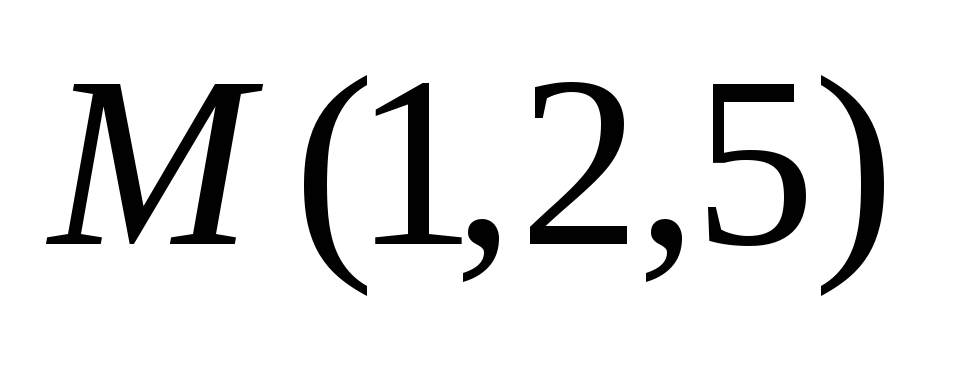 делит отрезок с концами
делит отрезок с концами
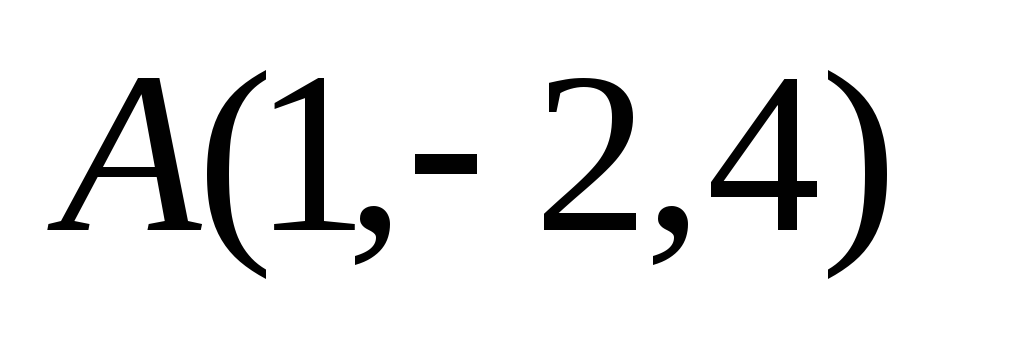 и
и
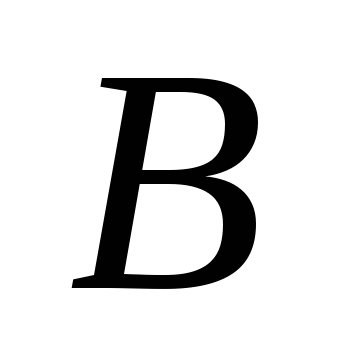 в отношении
в отношении
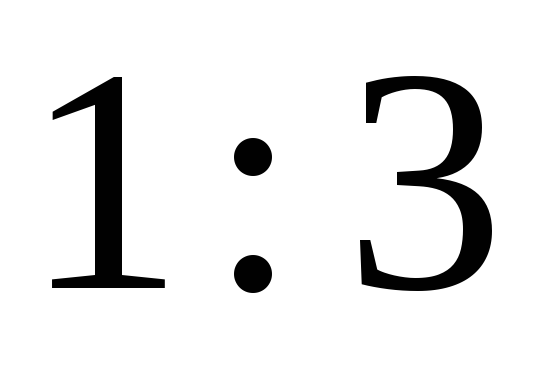 ,
считая от А.
Найдите координаты точки В.
,
считая от А.
Найдите координаты точки В. -
Даны векторы
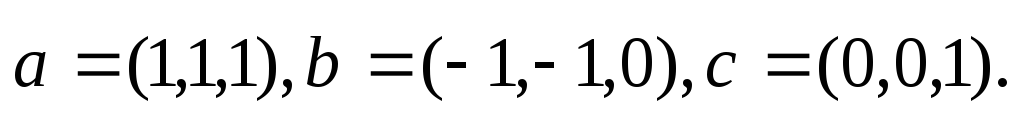 Справедливы утверждение:
Справедливы утверждение:
-
векторы
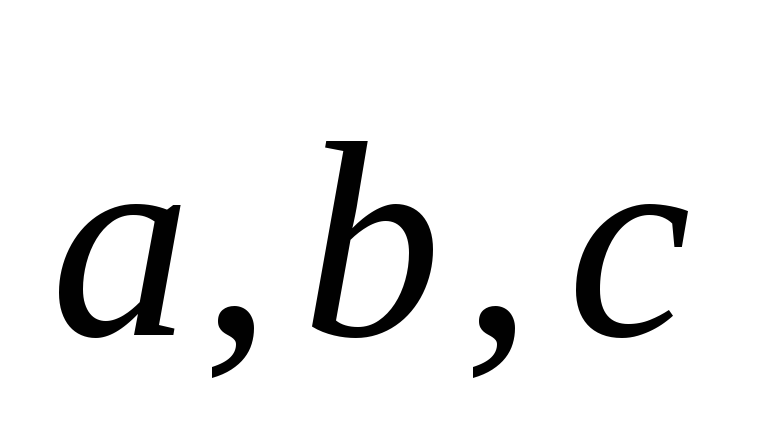 не образуют базис пространства;
не образуют базис пространства; -
векторы
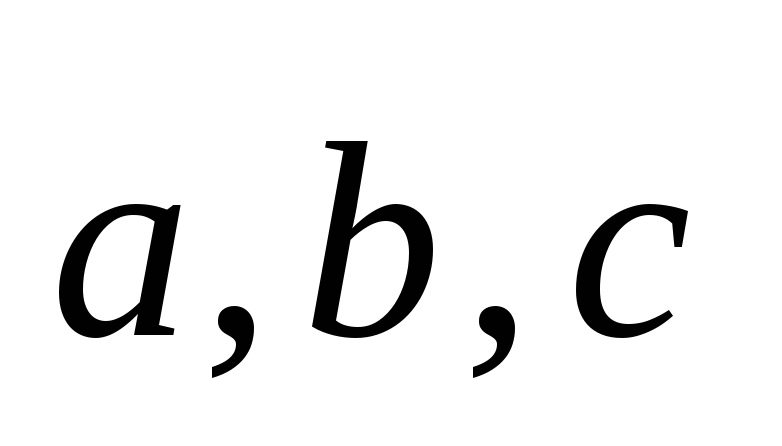 образуют ортогональный базис пространства;
образуют ортогональный базис пространства; -
векторы
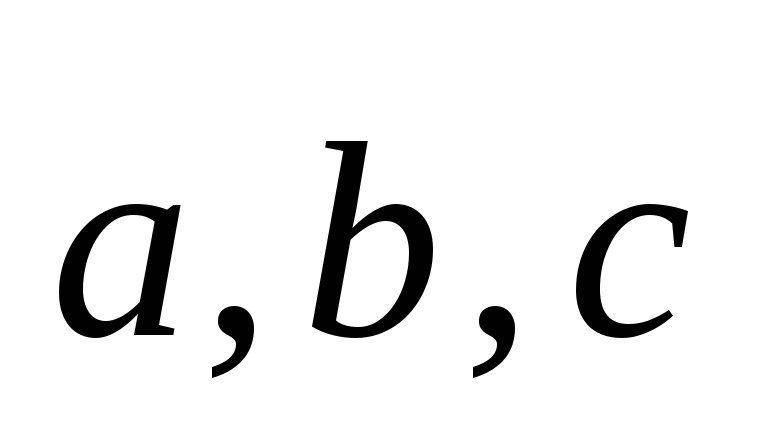 образуют нормированный базис пространства;
образуют нормированный базис пространства; -
векторы
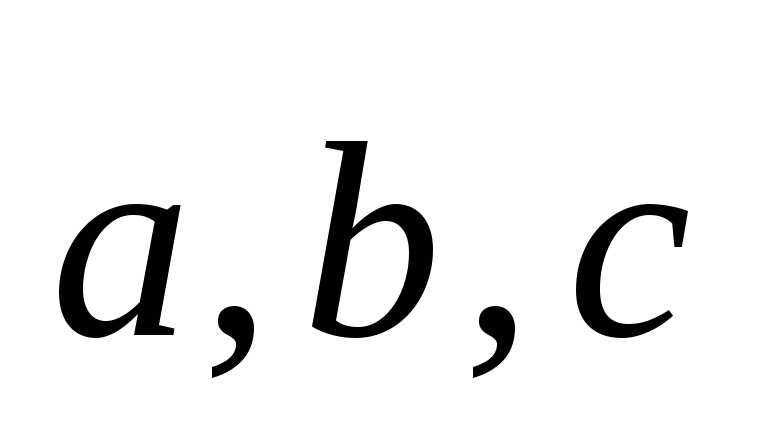 образуют базис пространства, который
не является ни ортогональным, ни
нормированным;
образуют базис пространства, который
не является ни ортогональным, ни
нормированным; -
нет правильного утверждения.
-
Известно, что
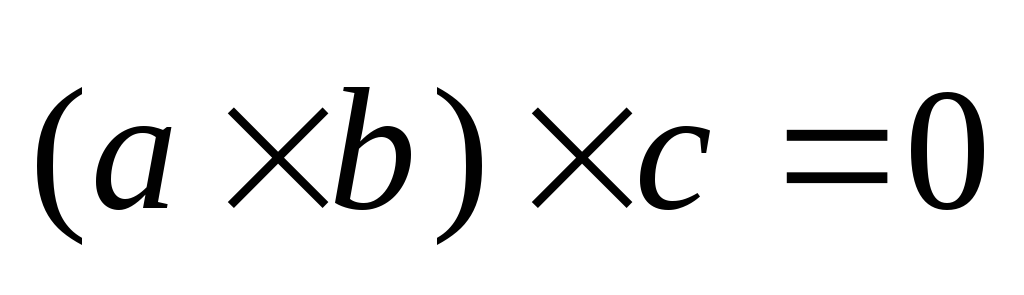 ,
тогда обязательно: А)
,
тогда обязательно: А)
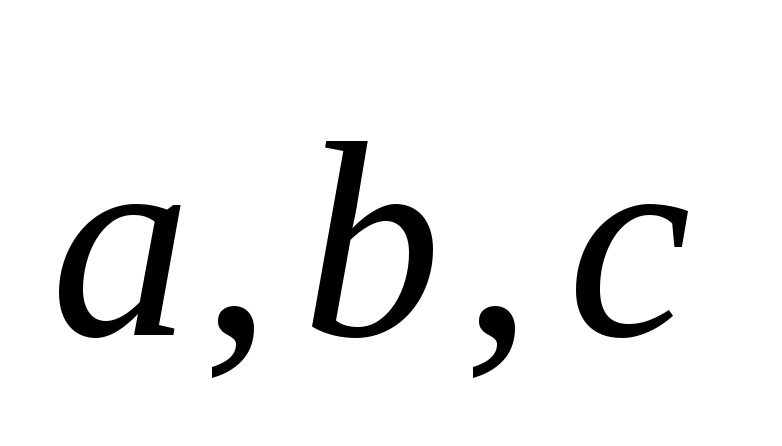 компланарны; B)
компланарны; B)
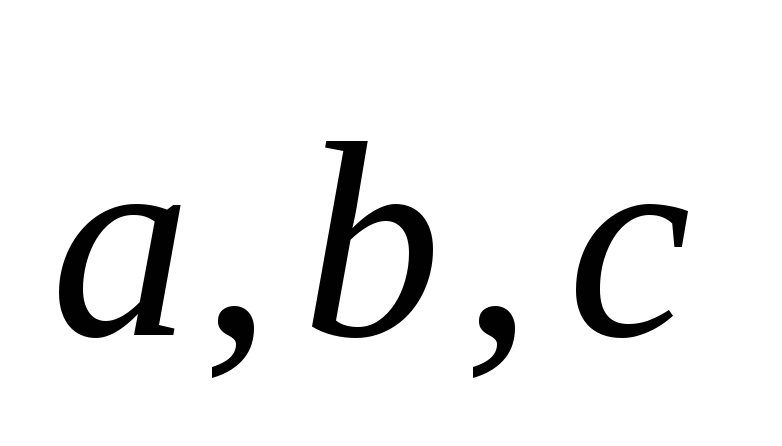 попарно ортогональны; С)
попарно ортогональны; С)
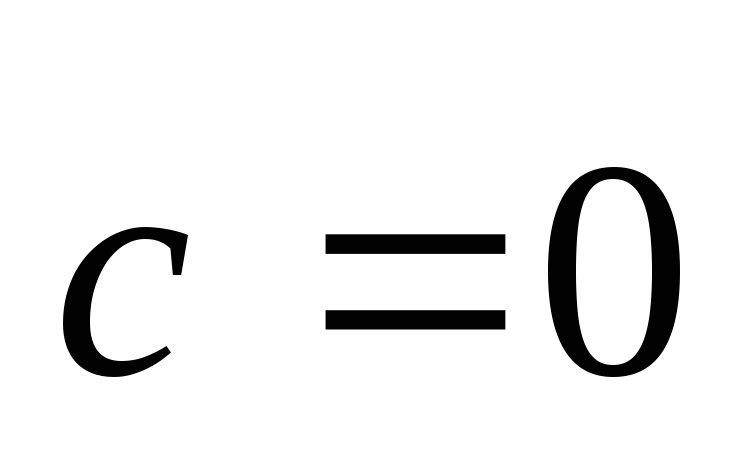 ;
D)
;
D)
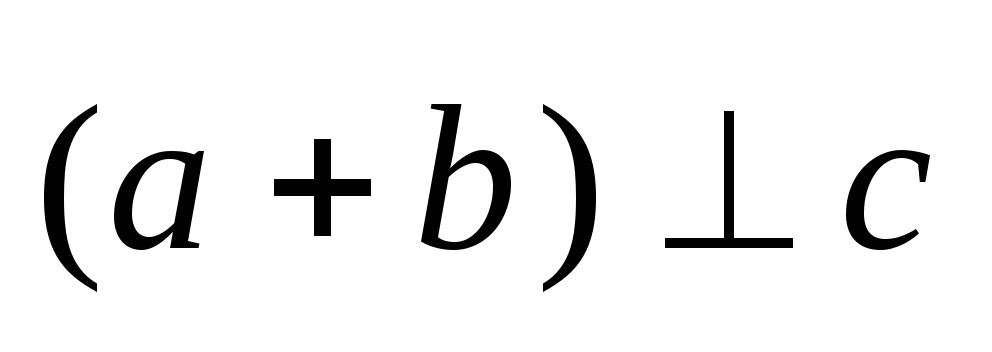 ;
;
E) нет правильного ответа.
-
Н
 а
рисунке изображена окружность, уравнением
которой в полярной системе координат
является:
а
рисунке изображена окружность, уравнением
которой в полярной системе координат
является:
-
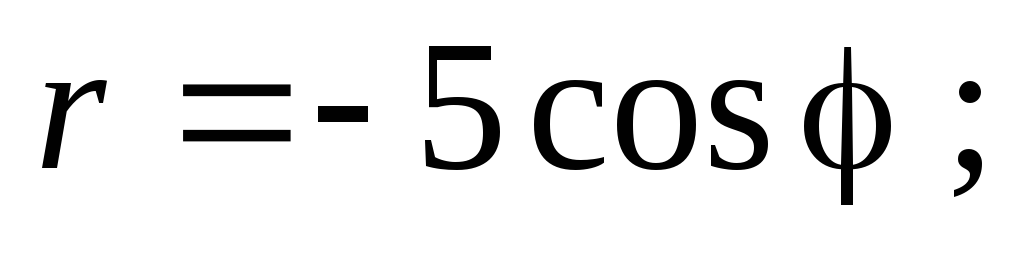 В)
В)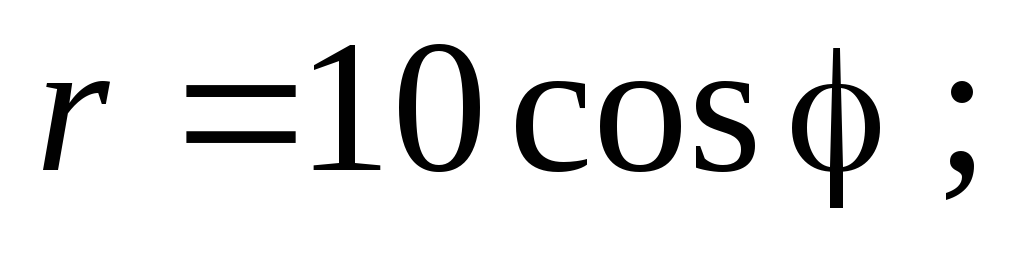 С)
С)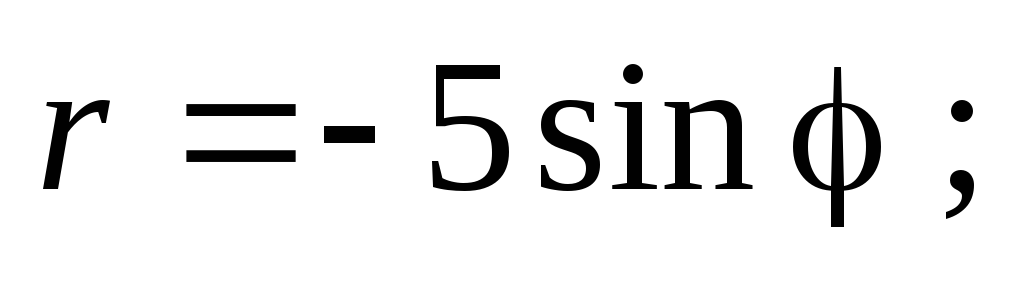 D)
D)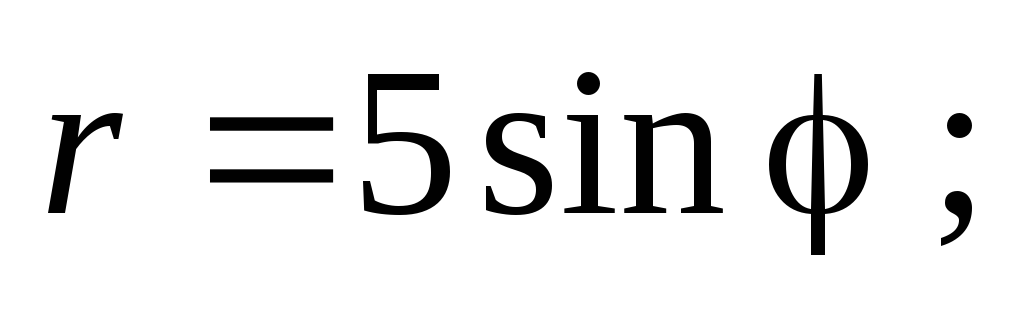 E)
нет правильного ответа.
E)
нет правильного ответа.
-
Две прямые
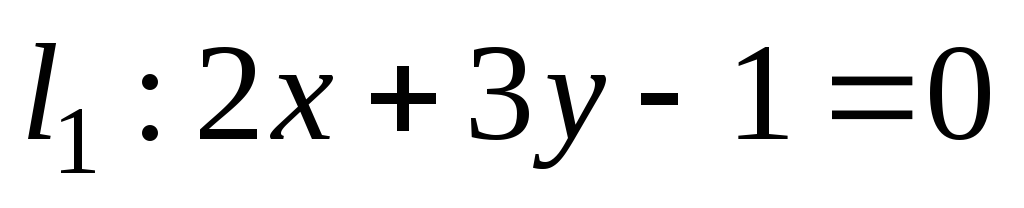 и
и
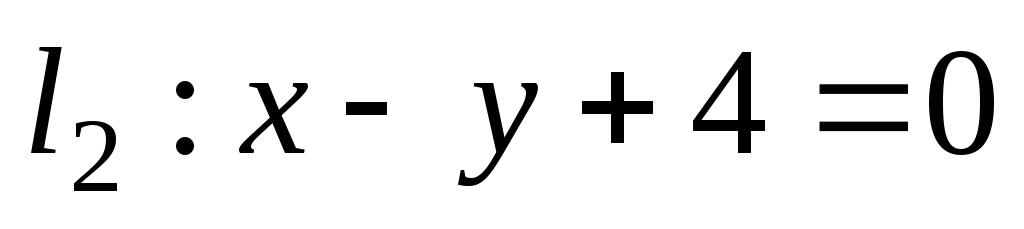 разбивают плоскость на 4 угла. Даны две
точки:
разбивают плоскость на 4 угла. Даны две
точки:
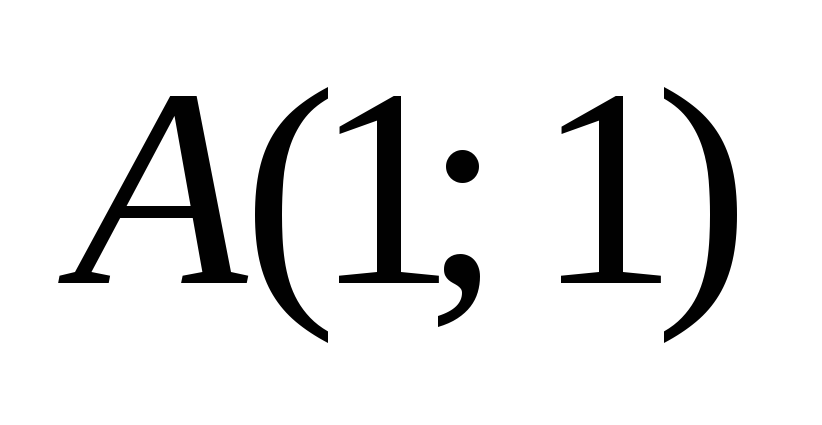 и
и
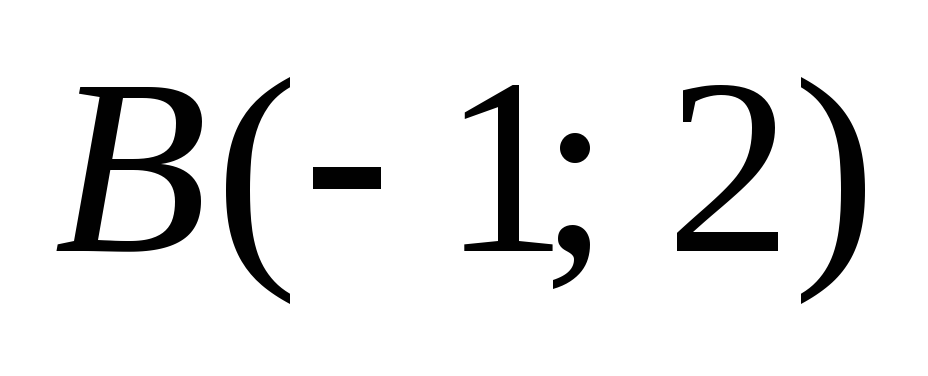 ,
тогда:
,
тогда:
-
точки А и В лежат в одном из 4-х углов;
-
точки А и В лежат в смежных углах;
-
точки А и В лежат в вертикальных углах;
-
одна или две из этих точек лежат на какой-нибудь из данных прямых;
-
нет правильного ответа.
-
Прямая, заданная параметрическими уравнениями
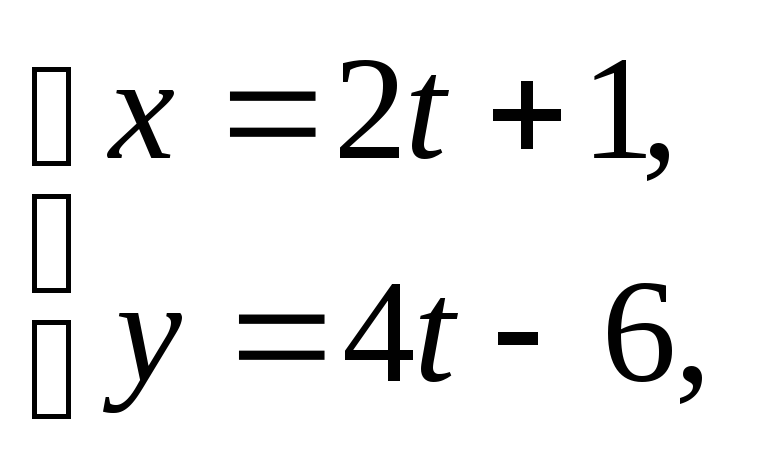 проходит
через точку А)
проходит
через точку А)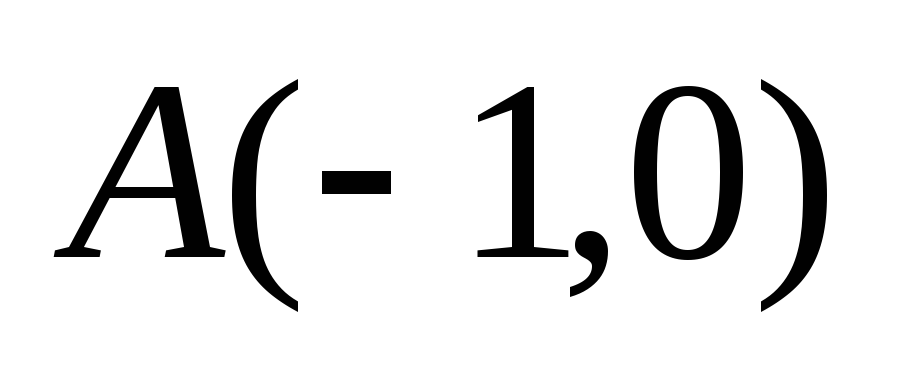 ;
В)
;
В)
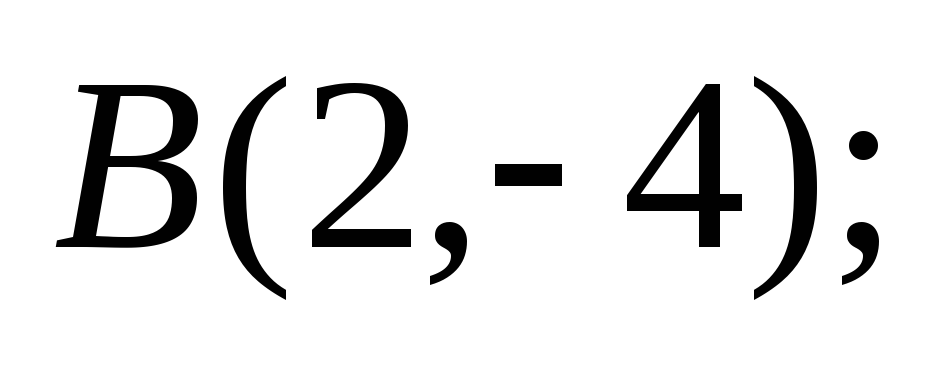 С)
С)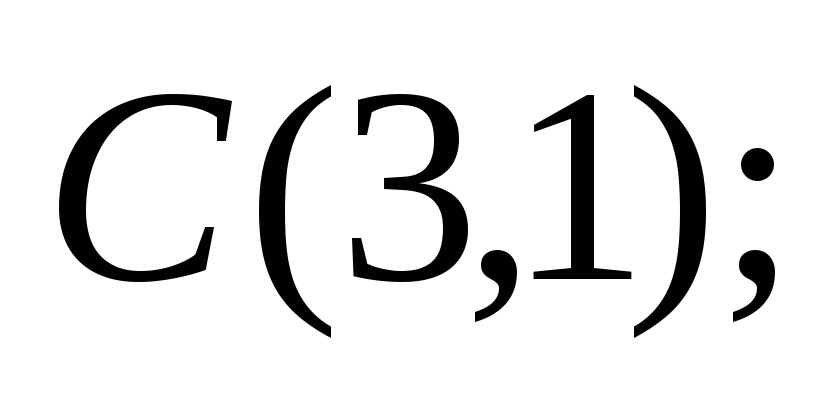 D)
D)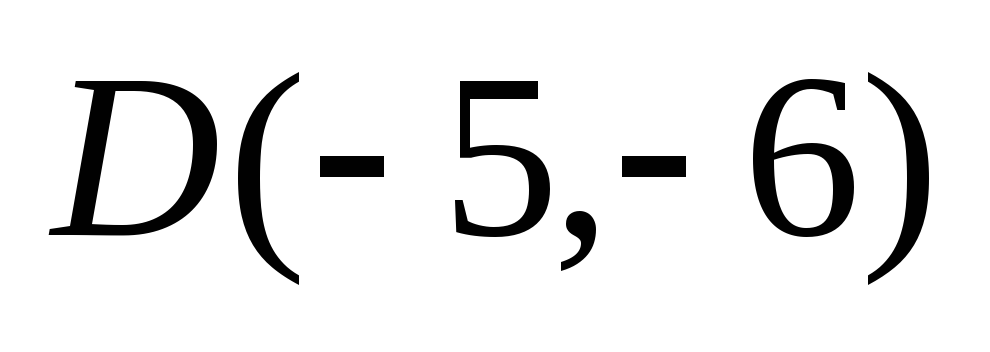 ;
Е) нет правильного ответа.
;
Е) нет правильного ответа. -
Директриса параболы имеет уравнение:
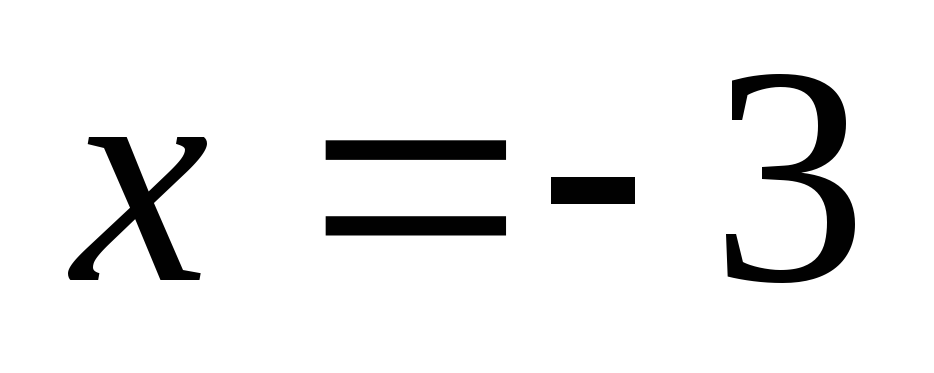 .
Найдите параметр параболы и ее
эксцентриситет.
.
Найдите параметр параболы и ее
эксцентриситет. -
Плоскость, задаваемая уравнением
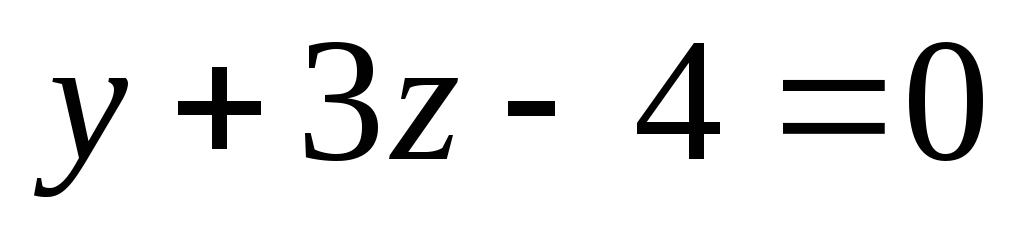 ,
А)
,
А)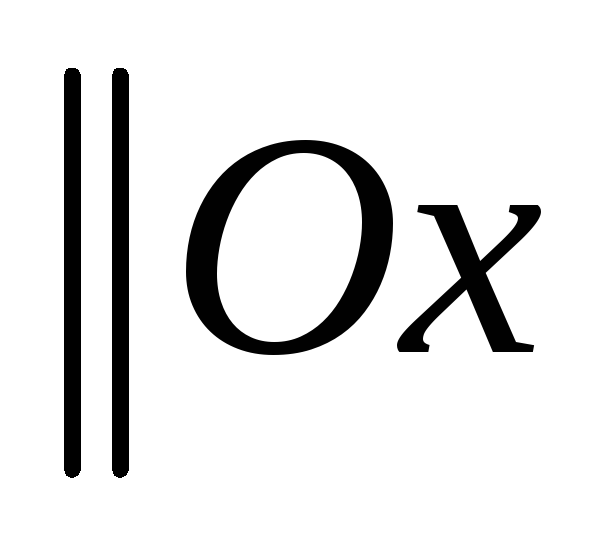 ;
В)
;
В)
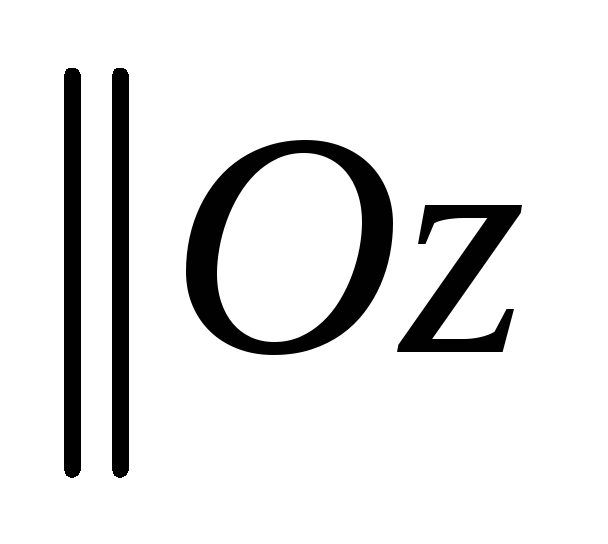 ;
С)
;
С)
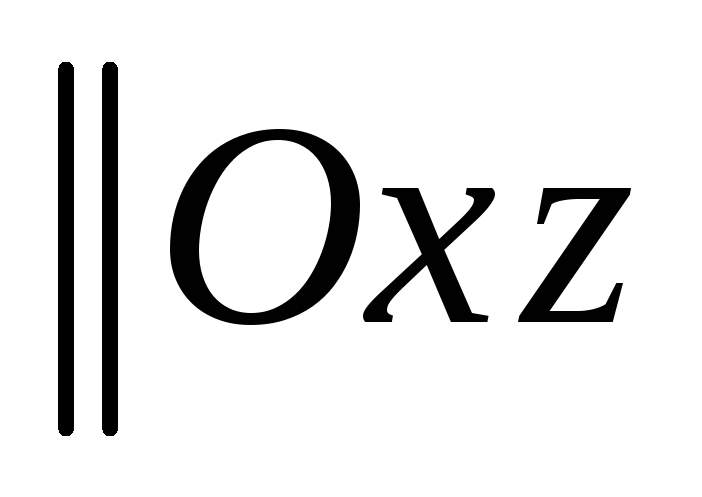 ;
D)
;
D)
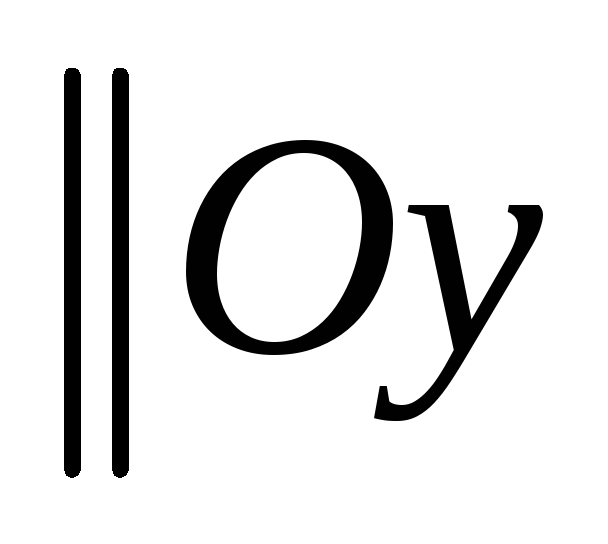 ; Е) нет правильного ответа.
; Е) нет правильного ответа.
-
Тетраэдр, ограниченный координатными плоскостями и плоскостью
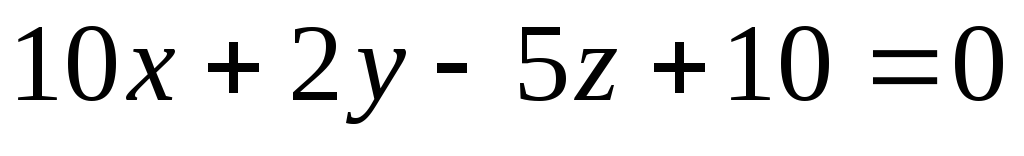 имеет объем А) 10; В)10/3; С) 5; D)
5/3; Е) нет правильного ответа.
имеет объем А) 10; В)10/3; С) 5; D)
5/3; Е) нет правильного ответа. -
Прямые
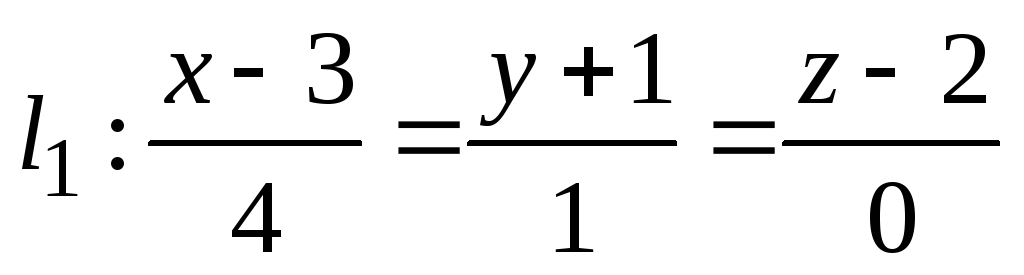 и
и
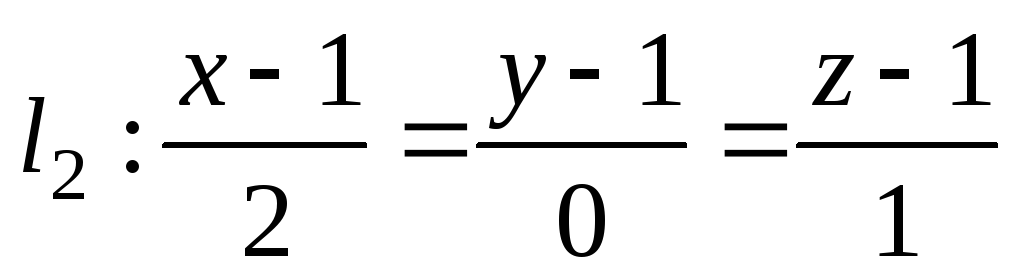
-
совпадают;
-
параллельны и не совпадают;
-
пересекаются;
-
скрещиваются;
E) нет правильного ответа.
-
Прямая задана общими уравнениями:
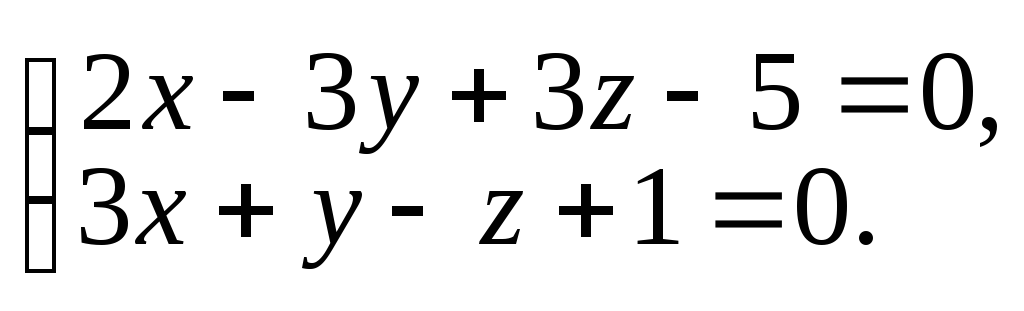 .
Найдите ее направляющий вектор.
.
Найдите ее направляющий вектор. -
Сечения поверхности второго порядка, заданной уравнением
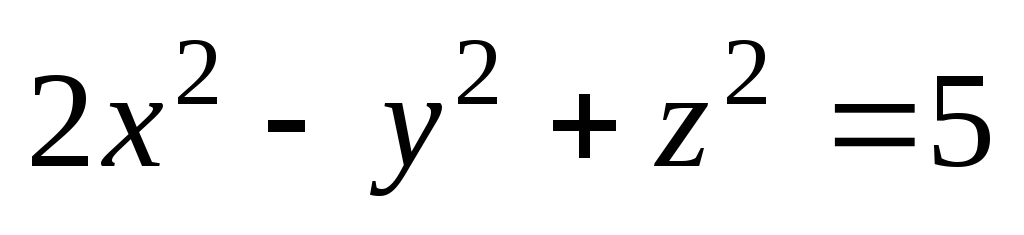 ,
плоскостями, параллельными плоскости
Оху,
являются;
,
плоскостями, параллельными плоскости
Оху,
являются;
-
окружностями;
-
эллипсами;
-
гиперболами;
-
параболами;
-
нет правильного ответа.
-
Выведите канонические уравнения прямой в пространстве.
Примечание:
За правильный ответ на вопрос №0 очки не присуждаются. В случае, когда нет правильного ответа на этот вопрос, работа далее не проверяется. В течение недели после оглашения результатов тестирования Вы имеете право выучить определение векторного произведения и сдать его. После этого Ваша работа будет проверена и оценена.
Вопросы по геометрии.
-
Необходимое и достаточное условие коллинеарности двух векторов.
-
Необходимое и достаточное условие компланарности трех векторов.
-
Теорема о единственности разложения по базису.
-
Теорема о вычислении проекции.
-
Необходимое и достаточное условие ортогональности двух векторов.
-
Выражение скалярного произведения через координаты векторов.
-
Выражение векторного произведения через координаты векторов.
-
Теорема о смешанном произведении. Необходимое и достаточное условие компланарности векторов.
-
Выражение смешанного произведения через координаты векторов.
-
Различные виды уравнений прямой на плоскости (10).
-
Взаимное расположение двух прямых на плоскости.
-
Угол между прямыми.
-
Расстояние от точки до прямой.
-
Различные виды уравнений плоскости в пространстве (5).
-
Угол между плоскостями.
-
Расстояние от точки до плоскости.
-
Различные виды уравнений прямой в пространстве (4).
-
Взаимное расположение двух прямых в пространстве.
-
Угол между прямыми в пространстве.
-
Расстояние от точки до прямой в пространстве.
-
Взаимное расположение прямой и плоскости в пространстве.
-
Угол между прямой и плоскостью в пространстве.
-
Преобразование декартовых координат при переносе начала координат.
-
Преобразование декартовых координат при повороте координатных осей. Матрица поворота.
-
Вывод канонического уравнения параболы.
-
Построение поверхностей второго порядка (эллипсоида, однополостного м двуполостного гиперболоидов, конуса вторго порядка, эллиптического и гиперболического параболоидов) методом сечений.
Вопросы по геометрии.
-
Необходимое и достаточное условие коллинеарности двух векторов.
-
Необходимое и достаточное условие компланарности трех векторов.
-
Теорема о единственности разложения по базису.
-
Теорема о вычислении проекции.
-
Необходимое и достаточное условие ортогональности двух векторов.
-
Выражение скалярного произведения через координаты векторов.
-
Выражение векторного произведения через координаты векторов.
-
Теорема о смешанном произведении. Необходимое и достаточное условие компланарности векторов.
-
Выражение смешанного произведения через координаты векторов.
-
Различные виды уравнений прямой на плоскости (10).
-
Взаимное расположение двух прямых на плоскости.
-
Угол между прямыми.
-
Расстояние от точки до прямой.
-
Различные виды уравнений плоскости в пространстве (5).
-
Угол между плоскостями.
-
Расстояние от точки до плоскости.
-
Различные виды уравнений прямой в пространстве (4).
-
Взаимное расположение двух прямых в пространстве.
-
Угол между прямыми в пространстве.
-
Расстояние от точки до прямой в пространстве.
-
Взаимное расположение прямой и плоскости в пространстве.
-
Угол между прямой и плоскостью в пространстве.
-
Преобразование декартовых координат при переносе начала координат.
-
Преобразование декартовых координат при повороте координатных осей. Матрица поворота.
-
Вывод канонического уравнения параболы.
-
Построение поверхностей второго порядка (эллипсоида, однополостного м двуполостного гиперболоидов, конуса вторго порядка, эллиптического и гиперболического параболоидов) методом сечений.
