
- •Дифференцируемость в точке. Связь существования производной.
- •Дифференцируемость в точке связь с непрерывностью.
- •Дифференцируемость в точке его геометрический смысл
- •Теорема Лагранжа
- •Раскрытие неопределённости . Правило Лопиталя.
- •Монотонность функции на промежутках. Исследование функций на монотонность
- •1. Монотонность функции.
- •Экстремумы функции.
- •Выпуклость функций
- •Асимптоты графика функции. Необходимое и достаточное условие существования наклонных асимптот.
Производная, ее геометрический и физический смысл. Правила дифференцирования.
Производной функции у = f{x) в точке x0 называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю.
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке
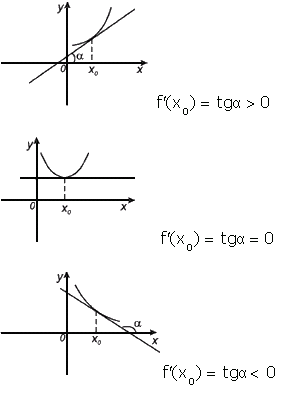
Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
![]()
Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то
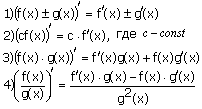
Производная сложной функции:
![]()
Определение Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е. limΔx→0α(Δx)=0.
Дифференцируемость в точке. Связь существования производной.
Теорема Для того, чтобы функция y=f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную. Доказательство
Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной функции в точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A.
Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A.
Если
для данного значения x приращение
функции Δy = f(x+Δx)
– f(x) можно
представить в виде Δy = A·Δx +
α, где α – бесконечно малая величина,
удовлетворяющая условию ![]() ,
т.е. если для функции y=f(x) существует
дифференциал dy=A·dx в
некоторой точке x,
то эта функция имеет производную в
точке x и f '(x)=А.
,
т.е. если для функции y=f(x) существует
дифференциал dy=A·dx в
некоторой точке x,
то эта функция имеет производную в
точке x и f '(x)=А.
Действительно,
имеем ![]() ,
и так как
,
и так как ![]() при
Δx→0,
то
при
Δx→0,
то ![]()
Дифференцируемость в точке связь с непрерывностью.
Если функция дифференцируема в точке, то она непрерывна в этой точке.
Доказательство. Пусть
функция у=f(x) дифференцируема
в точке х0.
Дадим в этой точке аргументу приращение Dх.
Функция получит приращение Dу.
Найдем ![]() .
.
![]() .
.
Следовательно, у=f(x) непрерывна в точке х0.
Следствие. Если х0 – точка разрыва функции, то в ней функция не дифференцируема.
Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.
Пример. у=|х| , х0=0.
Dх>0, ![]() ;
Dх<0,
;
Dх<0, ![]() .
.
В точке х0=0 функция непрерывна, но производной не существует.
Дифференцируемость в точке его геометрический смысл
Пусть функция f(x) дифференцируема в точке х0. Проведем касательную к графику этой функции в точке M0(x0, f(x0)) (рис. 1).
Угловой коэффициент касательной равен tg α = f '(x0), где α — угол между касательной и осью OX. При изменении абсциссы х0 на Δx приращение ординаты соответствующей точки касательной равно
|
Δx · tg α = f '(x0) · Δx ≡ df(x0). |
|
Таким образом, дифференциал функции f(x) в точке х0 равен приращению, которое получает линейная функция, графиком которой является касательная, при переходе из точки x0 в точку x0 + Δx.
Дифференцируемость в точке инвариантность формы дифференциала


![]()
Дифференцирование показательно степенной функции.
Показательно-степенной функцией называется функция вида y = uv, где u=u(x), v=v(x).
Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции.
![]()
![]()
Дифференцирование функции заданной неявно.
|
Пусть значения переменных х и у связаны уравнением F(x, y) = 0. (1) Если функция y = f(x), определенная на некотором интервале (а,в), такая, что уравнение (1) при подстановке в него вместо у выражения f(x) обращается в тождество, то говорят, что уравнение (1) задает функцию y = f(x) неявно или что функция y = f(x) есть неявная функция. Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, то есть не представляя в виде y = f(x), так как часто это преобразование бывает технически сложным или невозможным. Для нахождения производной у'х неявной функции, нужно продифференцировать по х обе части равенства (1), учитывая, что у есть функция от х. Затем из полученного равенства выразить у'х. |
Производные высших порядков, и их свойства.
Производные высших порядков
Пусть
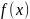 дифференцируемая
на промежутке
дифференцируемая
на промежутке
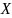
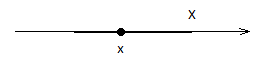
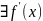 ,
если она дифференцируема на промежутке
,
если она дифференцируема на промежутке
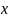 ,
то существует ее производная на
промежутке
.
,
то существует ее производная на
промежутке
.
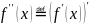
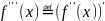
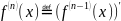
Свойства
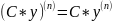 ,
,
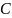 – константа
– константа
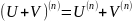
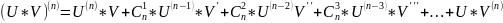 (формула
Лейбница).
(формула
Лейбница).
Повторное дифференцирование функции, заданной параметрически.
Пусть
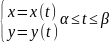
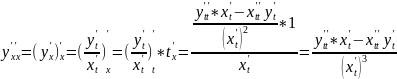
Дифференциалы высших порядков, их свойства.
Дифференциалы высших порядков
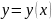 определена
на промежутке
определена
на промежутке
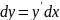
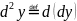
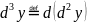
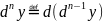
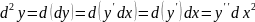
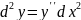
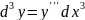
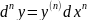
Дифференциалы высших порядков не обладают инвариантностью
Пусть
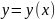 ,
где
– независимая переменная
,
где
– независимая переменная
,
по
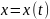
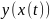 сложная
функция
сложная
функция
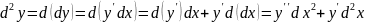
Дифференциал не совпадает.
Свойства
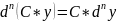
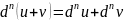
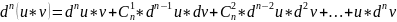 (Формула
Лейбница)
(Формула
Лейбница)
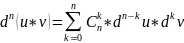
Доказательство
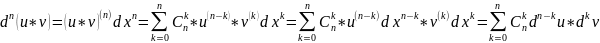
Теорема Ферма
Пусть
дифференцируема
на промежутке
и
в некоторой точке
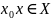 принимает
наибольшее значение
принимает
наибольшее значение
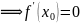
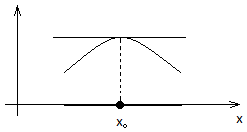
Доказательство
Пусть
принимает
в точке
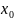 наибольшее
значение
наибольшее
значение
Пусть
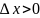
![]()
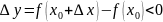
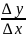 <0
<0
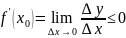
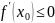
Пусть
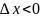
![]()
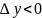
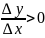
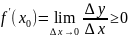
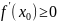
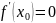
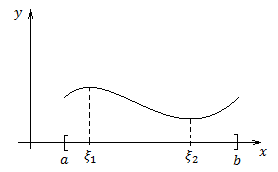
Теорема Ролля.
Пусть
– непрерывна на
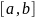 и
дифференцируема на
и
дифференцируема на
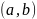 и
пусть
и
пусть
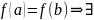 по
меньшей мере одна точка
по
меньшей мере одна точка
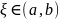 ,
в которой
,
в которой
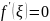
Доказательство
По
условию
непрерывна
на
,
тогда
достигает
на
своей точной верхней и нижней граней,
т. е. точки
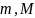 являются
наименьшим, наибольшим значениями
соответственно.
являются
наименьшим, наибольшим значениями
соответственно.
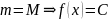
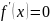 в любой точке
в любой точке
Пусть
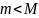 тогда
одно из них достигается во внутренней
точке
тогда
одно из них достигается во внутренней
точке
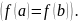
Пусть,
например,
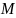 достигается
во внутренней точке
достигается
во внутренней точке
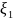 ,
по теореме Ферма
,
по теореме Ферма
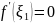 .
.
