Решение

1)Используя нижеперечисленные формулы заполним таблицу. Так как в таблице представлены изменение по сравнению с предыдущим годом будем использовать цепные показатели.

Абсолютный прирост (цепной):

Темп роста:

Темп прироста:

Темп прироста можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100 %.

Т акже мы будем использовать формулу абсолютного значения одного процента прироста, который рассчитывается как отношение абсолютного прироста к темпу прироста за тот же период времени:

Получилась следующая таблица:

Год	Импорт, млрд. долл. США	Изменение по сравнению с предыдущим годом
		абсолютный прирост, млрд. долл.	темп роста, %	темп прироста, %	абсолютное значение1 % прироста, млрд. долл.
2001	53,8	-	-	-	-
2002	61	7,2	113,383	13,383	0,538
2003	76,1	15,1	124,754	24,754	0,610
2004	97,4	21,3	127,989	27,9895	0,760
2005	125,3	27,9	128,644	28,644	0,974
2006	163,9	38,6	130,806	30,806	1,253

2)Рост объёма импорта происходило с наибольшей абсолютной скоростью в 2006году т.к абсолютную скорость роста определяют по показателю абсолютный прирост а в 2006 году он наибольший.

Рост объёма импорта происходило с наибольшей относительной скоростью в 2006 году т.к относительная скорость роста определяют по показателю темп роста а в 2006 году он тоже наибольший.

3) Для обобщающей характеристики динамики объёма импорта внешней торговли РФ определим средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.

С редний уровень ряда находим по формуле средней арифметической простой:

где - абсолютные уровни ряда;

- число уровней ряда

П олучим:

Средний абсолютный прирост рассчитывается по формуле

,

где n – число цепных абсолютных приростов.

Получаем:

Средний темп роста равен:

Тогда средний темп прироста равен:

3. График изменение импорта

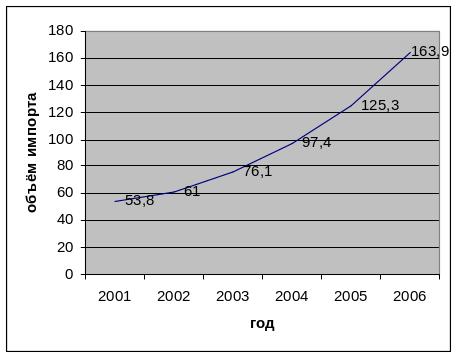
График изменения абсолютного прироста

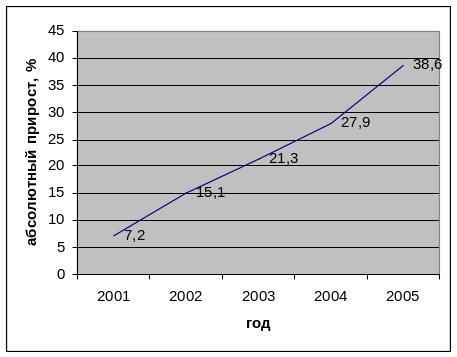
4) Вывод: Объём импорта внешней торговли РФ имеет тенденцию к увеличению, что хорошо видно из таблицы и графиков представленных выше.

Задача № 5

Средняя месячная заработная плата работников в отчетном периоде составила 9620 р., что на 10 % превышало соответствующий показатель базисного периода. Численность работников за этот же период сократилась на 2 % и составила 132 человека.

Определите, как изменился фонд заработной платы за этот период в абсолютном и относительном выражении в целом и за счет отдельных факторов: изменения средней заработной платы и изменения численности работников.

Решение

Сначала составим таблицу с данными из условия задачи для более удобного вычисления.

период	Средняя месячная зарплата, руб	Средняя месячная зарплата, %	Численность работников	Численность работников, %
Базисный		100		100
Отчётный	9620	110	132	98

Вычислим среднемесячную зарплату в базисном периоде

Вычислим численность работников в базисном периоде

Изменение фонда заработной платы в относительном выражении будем высчитывать по формуле

Фонд заработной платы увеличился на 7,56%

Изменение фонда заработной платы в абсолютном выражении будет равно

Изменение фонда заработной платы зависит от двух факторов: среднемесячной заработной платы и численности работников.

В зависимости от изменения численности работников (это количественный показатель):

За счёт уменьшения численности работников фонд заработной платы экономит 26235рублей.

В зависимости от изменения среднемесячной зарплаты(это качественный показатель):

За счёт увеличения среднемесячной зарплаты фонд заработной платы тратит на 26235рублей больше.

Задача № 6

По данным задачи № 1:

1) постройте линейное уравнение регрессии, проверьте значимость уравнения и его параметров с вероятностью 90 %;

2) дайте интерпретацию коэффициента регрессии, определите коэффициенты корреляции и эластичности;

3) на графике изобразите теоретическую линию регрессии;

4) сопоставьте результаты аналитической группировки и корреляционно-регрессионного анализа. Сделайте выводы.

	Соотношение мужчин и женщин, (х)	Смертность, ‰, 2004 (у)	xy
1	0,86	16,0	13,76	0.7396
2	0,87	16,0	13,92	0,7569
3	0,88	14,3	12,58	0,7744
4	0,93	10,1	9,39	0,8649
5	0,94	9,8	9,21	0,8836
6	0,94	9,4	8,84	0,8836
7	0,94	8,4	7,9	0,8836
8	0,94	9,5	8,93	0,8836
9	0,95	10,0	9,5	0,9025
10	0,95	8,1	7,7	0,9025
11	0,97	8,2	7,95	0,9409
12	0,99	4,5	4,46	0,9801
13	0,9961	5,0	4,98	0,9922
14	1,004	7,2	7,23	1,008
15	1,02	6,2	6,3	1,04
16	1,043	6,5	6,78	1,088
17	1,063	6,4	6,8	1,13
18	1,072	7,5	8,04	1,149

Итого

17,3581

163,1

154,27

16,0638

Решение