14

Задания на выполение лабораторных работ

по дисциплине

«Дискретная математика»

Лабораторная работа № 1

Представление и выполнение операций над множествами

Цель: Получить навыки в задании множеств и операций с ними.

Если все элементы множе­ства А принадлежат также множеству В, а все элементы множества В принадлежат также множеству А, то А = В.

Все элементы множества Z могут принадлежать также множеству А. Тогда множество Z именуется подмножеством А. Для подмножества Z множества А принято обо­значение: Z А. Символ именуется «включение». Если не исключается возможность ситуации, когда Z = А, то для того чтобы акцентировать на этом внимание, пишут Z А, хотя это и не обязательно.

Принимая термин «подмножество», аксиому Z1 мож­но сформулировать следующим образом:

Z1: если В А и А В, то А = В.

Рассмотрим, в чем смысл этой аксиомы состоит в следующем.

Пусть А = {а₁, а₂} и В = {b_lt Ь₂} — множества. В соответ­ствии с введенным определением принадлежности эле­ментов множествам имеем а₁, а₂ А и b₁, b₂ В. Если при этом также выполнено a_v a₂ В и b₁, b₂ А, то, что А = В.

Иногда возникает вопрос: как определить принадлежность элементов одного множества другому множеству? Эта принадлежность может быть известна по условию задачи, либо установлена на основании ее дополнительных исследований, либо не определена. Пре­достерегая от возможных ошибок, отметим, что символ принадлежности имеет более высокий статус, чем сим­вол равенства. Поэтому из попарного равенства число­вых значений элементов двух различных множеств еще не вытекает их взаимная принадлежность.

1. Метод диаграмм Эйлера – Венна:

: :

2. Метод принадлежности:

Два множества равны (М=N) тогда и только тогда, когда множество М является подмножеством множества N и множество N является подмножеством множества M, т.е.

1. 

;

2. 

.

3. Метод характеристической функции:

Для произвольных множеств А и В существует единственное множество С, элементами которого являются все элементы множества А и все эле­менты множества В и которое никаких других элемен­тов больше не содержит.

Множество С именуется суммой или объединением множеств А и В. Символ операции объединения: .

Из аксиомы Z3 следует, что сумму множеств А и В можно записать в виде

С=А В. (1.2)

При этом из единственности С следует выполнение свойств:

А В = В А — коммутативность и

(А В) D = А (В D) — ассоциативность для любой тройки множеств, входящих в объединение.

Представляет интерес рассмотреть в качестве приме­ров три случая: когда множества А и В не имеют общих элементов, когда все элементы общие и когда только некоторые элементы этих множеств являются общими.

Если множества А и В не имеют общих элементов, их объединение строится наиболее просто. Пусть элемента­ми множеств А и В являются точки некоторого одного и того же отрезка числовой оси: А = {1, 2}, В = {3, 4, 5, 6}. Тогда С = А В = {1, 2, 3, 4, 5, 6}.

Если у множеств А и В все элементы общие, например, в условиях предыдущего примера А = {1, 2, 3}, B = {1, 2, 3}, то на основании Zl: A В = {1, 2, 3}.

Пусть у множеств А и В общие только некоторые эле­менты. Положим А = {1, 2, 3, 4}, В = {1, 2, 3, 4}, и пусть при этом известно, что принадлежат обоим множествам элементы со значениями 2 и 3. В таком случае остальные элементы этих множеств необходимо отметить как при­надлежащие разным множествам. Условимся, например, индексировать их символами исходных множеств. Тогда С = А В = {1^a, 1^b, 2, 3, 4^a, 4^b|.

Такая ситуация может иметь место, например, при слиянии таблиц, когда у таблиц А и В колонки 2 и 3 являются общими, а остальные — нет.

Для наглядности операцию объединения множеств можно интерпретировать диаграммой, предложенной ØЭйлером.

Если речь идет об объединении нескольких множеств, пишут: _аА и считают, что элемент, принадлежащий U А , принадлежит каждому из А .

С=А В

Теорема 1.1. Для любых двух множеств А и В суще­ствует единственное множество С, составленное из тех и только тех элементов, которые принадлежат как множе­ству А, так и множеству В.

Доказательство. Существование общих элементов у множеств А и В допускается по определению принад­лежности элемента множеству.

Если общий элемент единственен, то сразу же прихо­дим к заключению теоремы.

Если имеем пару общих элементов, то для построения множества С воспользуемся аксиомой Z2.

Если общих элементов более двух, то, последовательно применяя к ним аксиому пары, получим систему множеств, каждое из которых содержит предыдущее множество и последующий общий элемент. Теперь для построения мно­жества С достаточно воспользоваться аксиомой суммы, применяя ее ко всем множествам данной системы.

Если же A и В не имеют ни одного общего элемента, то множество С также определяется единственным обра­зом — как множество, не содержащее ни одного элемен­та. Теорема доказана.

Множество, не содержащее ни одного элемента, назы­вается пустым. Для него принят специальный символ: Ø. Иногда этот символ в литературных источниках заменя­ют символами О либо { }. Смысл их тот же.

Для произвольного семейства множеств А имеет мес­то следующая теорема , которую мы приводим без доказательства.

Для произвольного семейства множеств А существует единственное множество С, составленное из тех и только тех элементов, которые принадлежат всем множествам семейства А.

Множество С, определенное теоремами 1.1 и 1,2, на­зывается произведением либо, что чаще, пересечением множеств, на которых оно построено. Это понятие столь же часто встречается в теории множеств, что и понятие суммы. Для обозначения операции пересечения множеств принят символ:

Операция пересечения множеств А и В записывается следующим образом:

С =А В. (1.3)

Из единственности множества пересечения вытекают свойства этой операции:

А В =В А — коммутативность для любой пары и

(А В) D = А (В D) — ассоциативность для любой тройки пересекающихся множеств.

Пусть А и В — произвольные множества. Построим множество тех элементов А, которые не принадлежат В. Тот факт, что такое множество существует и единствен­но, доказывается точно так же, как и в теореме 1.1.

Полученное множество называется разностью множеств А и В. Для представления разности множеств принята операция, которая обозначается символами: «-» либо “\”.

Например, запись

С=А~В (1.4)

или, что то же, С = А \ В имеет смысл: “те элементы из А, что не в В”.

Операция разности множеств, по своему определению, не ассоциативна и не коммутативна. В частности, из определения этой операции также следует, что должно быть выполнено

(А-В) (В-А) = 0. (1.5)

Часто в рамках некоторой математической теории фик­сируется множество, содержащее все другие множества как объекты этой теории. Такое множество называют уни­версальным. Обозначают его, как правило, наименовани­ем данного фиксированного множества.

Так, пусть I — любое универсальное множество и А I. Построим разность I - А. Ясно, что I - А I. Такая разность множеств именуется дополнением. Любое подмножество универсального мно­жества называется его собственным подмножеством.

Существенный интерес в теории множеств представ­ляет объединение множеств (А - В) (В - А). Это мно­жество называется симметрической разностью множеств А и В. Для обозначения симметрической разности при­нят символ , т. е.

А В = (А-В) (В-А). (1.6)

То, что эта операция коммутативна, вытекает непо­средственно из ее определения формулой (1.6). Ассоци­ативность не очевидна, но также имеет место.

В рамках данной теории можно продолжать введение все новых операций над множествами. Однако перед этим естественно дать ответ на вопрос: не является ли уже введенная система операций избыточной? Избыточ­ность будем понимать в смысле существования на мно­жестве всех введенных операций непустого подмноже­ства, через элементы которого можно выразить все ос­тальные операции исходного множества.

Рассмотрим этот вопрос.

Теорема 1.3. Пусть А и В — любые множества. Тогда

А В = (А В) (А В) (1.7)

и при этом множества (А B) и (А В) не пересекаются.

Oперация суммы множеств может быть единственным образом выражена через опера­ции симметрической разности и пересечения.

Аналогично ,

А-В=А (А В). (1.8)

Из соотношений (1.7) и (1.8) видно, что все ранее вве­денные операции можно истолковать в терминах опера­ции пересечения и симметрической разности.

Такой подход получил фундаментальное применение в различных областях математики: теории интегрирова­ния, общей теории меры, теории вероятностей и других.

Основанием для его развития явилось понятие кольца множеств.

Непустая система множеств С называется кольцом множеств, если она замкнута относительно операций пересечения и симметрической разности:

если А, В С, то А В С;

если А, В С, то А B С.

Ясно, что кольцо множеств ассоциативно, коммута­тивно и его нулем служит пустое множество.

В кольце может существовать единица. Под единицей по­нимают такое множество Z, что А Z =А для любого А С.

В частности, пусть D С — множество, содержащее все другие элементы системы С, кроме самого себя, и не содержащее никаких других множеств. Тогда А D = А для любого А е С и, следовательно, D = Е.

Для кольца с единицей введено понятие алгебры мно­жеств.

Алгебраические вычисления в кольцах выполняются по правилам, аналогичным обычным арифметическим. При этом роль «суммы» играет операция , а роль «про­изведения» — операция .

B заключение отметим следующее. Рас­смотренные выше операции объединения, пересечения, разности и симметрической разности множеств, получен­ные исключительно на основе понятия принадлежности элемента множеству и аксиом Zl, Z2 и Z3, составляют основной арсенал операций теории множеств.

Задание

Выполнить на заданных множествах операции объединения, пересечения, симметрической разности, дополнения.

Лабораторная работа № 2 Представление отношений в эвм

Цель: Получить навыки задания отношений на декартовом произведении.

Допустим, что X и Y — произвольные множества. На основа­нии аксиомы пары составим множество X×Y всех упоря­доченных пар (х, у}, где х X, у Y.

Поскольку существует не более одного множества, содер­жащего в качестве элементов все пары (х, у), и только та­кие пары, то множество X×Y определено ими однозначно: X×Y = {(х, у}: х X, у У}.

Определенное в (1.9) множество именуется декарто­вым произведением множеств X и У.

В частности, не исключается случай, когда для каж­дого элемента множества X найдется равный ему элемент множества У и обратно. В таком случае декартово произведение именуется декартовым квадратом и обо­значается X².

Удобно употреблять для декартовых произведений геометрический язык. Элементы множества X×Y назы­вают точками, множества X и У — осями координат, элементы х — абсциссами, а элементы у — ординатами.

Пусть, например, X = {1, 2, 3} и У = {1, 2}. Соответ­ствующее декартово произведение

X×Y = {(1,1), (1, 2), (2,1), (2, 2), (3,1), (3, 2)}.

Это множество можно интерпретировать графическим построением

Если задана система п множеств: X_lt Х₂,..., Х_п, то де­картовым произведением Х₁хХ₂,...,хХ_п множеств назы­вается множество всех упорядоченных п-ок, составлен­ных из элементов этих множеств.

Отношениями называются любые непустые подмно­жества декартовых произведений.

Так, допустим, R — отношение, т. е. R X×Y. Вместо (х, у} R чаще пишут xRy, что означает: «x находится в отноше­нии R к у» или «отношение R имеет место между х и у». Отношение {(х, у}: yRx] называется обратным к R и обо­значается R^c.

Рассмотрим примеры отношений.

Определим на множестве всех точек отноше­ние R например следующим образом:

R = {(1,2), (3, 2}}.

Этому отношению можно придавать самый различный смысл. Например, объявить элементы множества R как концы некоторой дуги. В этом случае xRy означает: «эле­менты х и у находятся в отношении друг к другу как координаты одного из концов некоторой кривой».

Можно, например, объявить, что множество точек, определенных отношением R, и только они, окрашены в зеленый цвет. Тогда запись xRy означает: х и у — координаты зеленой точки. Остальные точки в нашем примере будут выделены отношением

Отношением эквивалентности называется всякое от­ношение R, которое удовлетворяет трем условиям:

рефлексивности: xRx,

симметричности: если xRy, то и yRx,

транзитивности: если xRy и yRz, то и xRz для любых (х, у) R.

Пусть X — любое множество, представленное в виде семейства А непустых, непересекающихся подмножеств

X_1, X₂,... Х_n Х и таких, что X_:U Х₂ U X_n = X, Такое семейство А = {Х_1,Х₂, ... X n}J - называется разбиением мно­жества X.

Например, если X = {1, 2, 3, 4, 5, 6}, то в качестве разбиения X можно принять семейство подмножеств А = { Х_1, Х₂, Х₃}, где Х₁ = {I, 2}, Х₂ = {3, 4}, а Х₃ = {5, 6}. Каждое их этих подмножеств не пусто, но пусто любое их попарное пересечение. Сумма же этих множеств со­ставляет все X.

Задание.

Задать декартово произведение. На нем задать отношение. Определить, является ли оно функцией и, если да, определить сурьективность, инъективность и биективность.

Лабораторная работа № 3

Унарные и бинарные операции над графами.

Цель: Получить навыки в задании операций над графами.

Бинарным отношением на множестве называется любое подмножество множества , состоящего из всевозможных упорядоченных пар элементов множества . Каждому такому отношению можно поставить в соответствие граф отношения . Сравнивая с тем, что говорилось выше об определениях различных типов графов, видим, что понятие бинарного отношения эквивалентно понятию ориентированного графа с петлями. Другие типы графов без кратных ребер - это частные виды бинарных отношений. Отношение называется рефлексивным, если для любого пара принадлежит , и антирефлексивным, если ни одна такая пара не принадлежит . Отношение называется симметричным, если из следует, что . В графе антирефлексивного и симметричного отношения нет петель и для каждой пары вершин либо нет ни одного, либо есть два ребра, соединяющих эти вершины. Если в таком графе каждую пару ориентированных ребер, соединяющих одни и те же две вершины, заменить одним неориентированным ребром, то получится обыкновенный граф.

Граф G и орграф D изображены на рисунке. Найдем их матрицы смежности.

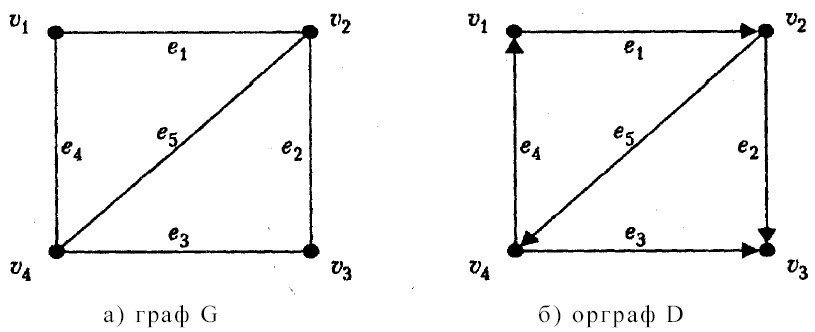
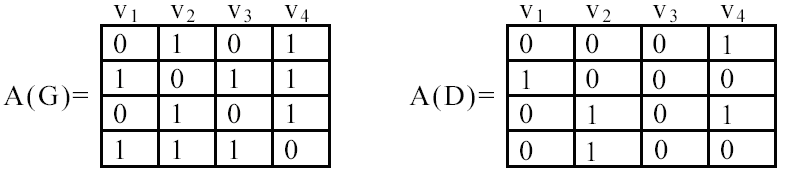
Матрица смежности для неоринтированного графа является симметричной.

Матрицу смежности можно ввести для мультиграфов: элемент aij матрицы A равен числу ребер (дуг) идущих из вершины vi к вершине vj.

Пусть G=(V,E) граф (орграф) с p-вершинами и q ребрами, т.е. V={v1,v2,…,vp}, E={e1,e2,…,eq}.

Матрицей инцидентности B(G) орграфа G называется матрица порядка p q, элементы которой вычисляются следующим образом:

Матрицей инцидентности B(G) графа G называется матрица порядка p q, элементы которой вычисляются следующим образом:

В каждом столбце матрицы инцидентности только два элемента не равны нулю (они равны 1).

Пример. Для графа G и орграфа D матрицы инцидентности будут выглядеть следующим образом:

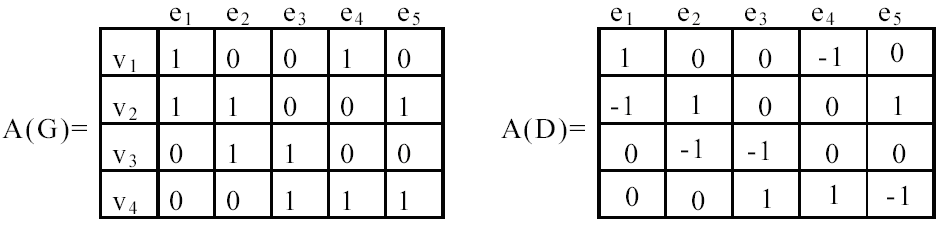
Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин называется списком смежности.

Для получения новых графов можно использовать разнообразные операции над графами. Здесь мы рассмотрим два вида операций - локальные, при которых заменяются, удаляются или добавляются отдельные элементы графа, и алгебраические, когда новый граф строится по определенным правилам из нескольких имеющихся.

1. Объединением двух графов G1 и G2 называется граф G=(V,E), где

V=V1 V2, E=E1 E2. Обозначение: G=G1 G2.

2. Пересечением двух графов G1 и G2 называется граф G=(V,E), где

V=V1 V2, E=E1 E2. Обозначение: G=G1 G2.

3. Симметрической разность (или суммой по модулю двух графов

G1 и G2 называется граф G=(V,E), где V=V1 V2, E=E1 E2

(E=E1 E2). Обозначение: G=G1 G2.

Пусть задан граф G=(V,E) c |V|=n (т.е. с n вершинами) и без петель.

На множестве вершин V построим полный граф Kn=(V,M).

4. Дополнением графа без петель G(V,E) называется граф G = (V, E \ M).

Простейшая операция - удаление ребра. При удалении ребра сохраняются все вершины графа и все его ребра, кроме удаляемого. Обратная операция - добавление ребра.

При удалении вершины вместе с вершиной удаляются и все инцидентные ей ребра. Граф, получаемый из графа удалением вершины , обозначают . При добавлении вершинык графу добавляется новая изолированная вершина. С помощью операций добавления вершин и ребер можно "из ничего", то есть из графа , построить любой граф.

Операция стягивания ребра определяется следующим образом. Вершины и удаляются из графа, к нему добавляется новая вершина и она соединяется ребром с каждой вершиной, с которой была смежна хотя бы одна из вершин .

Операция подразбиения ребра действует следующим образом. Из графа удаляется это ребро, к нему добавляется новая вершина и два новых ребра и Изображены исходный граф , граф , полученный из него стягиванием ребра и , полученный подразбиением того же ребра. В обоих случаях вновь добавленная вершина обозначена цифрой .

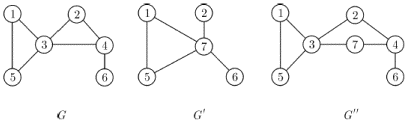
Задание

Выполнить операции объединения, пересечения и симметрической разности над графами

Лабораторная работа № 4

Вершинная и реберная связность графов

Цель: Получить навыки в работе с определением связности в графах.

Пусть в G есть контур. Рассмотрим любую дугу (a,b) в этом контуре. Тогда имеем а>b, но b>а по транзитивности, что противоречит строгости упорядочения.

Если орграф G(V,E) нe имеет контуров, то достижимость есть отношение строгого порядка.

1. Нет циклов, следовательно, нет петель, следовательно, достижимость антирефлексивна.

2. Если существуют пути из v в w и из w в u, то существует и путь из v в u. Следовательно, достижимость транзитивна.

3. Пусть достижимость — это не строгое упорядочение. Тогда существуют u,v такие, что u>v и v>u, то есть существует путь из v в u и из u в v. Следовательно, существует контур <u,v> <v,u>, что противоречит условию.

Если орграф не имеет контуров, то в нем есть вершина, полустепень захода которой равна 0.

Пусть такой вершины нет, тогда для любой вершины найдется вершина, из которой есть дуга в данную вершину. Следовательно, имеем контур против направления стрелок.

Двудольный граф (или биграф, или четный граф) — это граф G(V,E), такой что множество вершин V разбито на два непересекающихся множества V1 и V2 (т.е. V1»V2=V, V1…V2=«), причем всякое ребро из Е инцидентно вершине из V1 и вершине из V2 (то есть ребро соединяет вершину из V1 с вершиной из V2). Множества V1 и V2 называются долями двудольного графа. Если в двудольном графе, каждая вершина из V1 соединяется ребрами со всеми вершинами из V2, то граф называется полным двудольным графом. Если |V1|=n, и |V2|=m, то полный двудольный граф обозначается K_n,m.