
- •Перенос энергии электромагнитной волной. Вектор Пойнтинга и его взаимосвязь с объёмной плотностью энергии электромагнитного поля.
- •Распространение электромагнитных волн в веществе. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Электронная теория дисперсии.
- •Предмет и место в физике и технике
- •Геометрическая оптика: условия справедливости, четыре закона, явление полного внутреннего отражения света.
- •Расчёт эквивалентной схемы интерференционного опыта с двумя когерентными источниками света.
Расчёт эквивалентной схемы интерференционного опыта с двумя когерентными источниками света.
Эквивалентная схема интерференционного опыта представляет собой два точечных источника света S1 и S2, разделённых расстоянием d и удалённых на расстояние l от экрана, на котором наблюдается интерференционная картина.
Волны, приходящие от источников S1 и S2 в некоторую точку М на экране, имеют разность хода r = r1 – r2. Выразим эту разность хода через параметры схемы l, d и .
Т
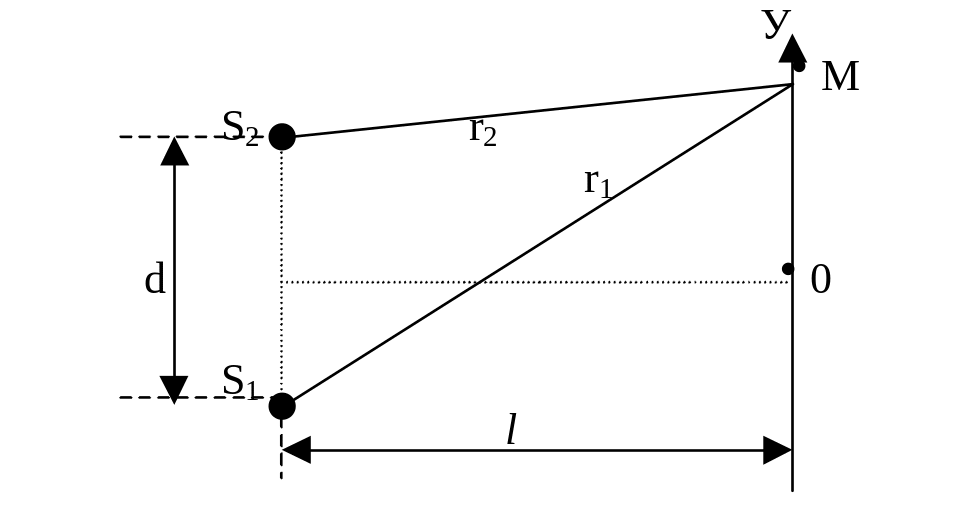
Обычно l d, и тогда (r1 + r2) 2l, а r = r1 – r2 уd/l.
Из условия максимума: r = m, получим координаты максимумов: уm макс = ml/d , где m .
В центре экрана, при у = 0 и m = 0, имеем светлое пятно (максимум) для любых длин волн. Остальные же (боковые) максимумы с номерами m 0 в белом1 свете окрашиваются, ибо положение уm макс зависит от длины волны .
Из условия минимума: r = r1 – r2 = (m + 1/2) следуют координаты минимумов уm мин = (m + ½)l/d.
Интерференционная картина характеризуется двумя параметрами:
- шириной b интерференционной полосы, равной расстоянию между соседними тёмными полосами (минимумами): b = уm, мин - уm-1, мин = l/d;
- расстоянием у между соседними полосами: у = уm макс - уm-1 макс = l/d.
Эти параметры равны друг другу. Имеем, так называемое, эквидистантное расположение полос.
Для заметного разноса у полос на экране удаление l экрана от источников должно быть много больше расстояния d между источниками света: l d.
Если какая-либо из волн (или обе) проходят часть или весь путь r1 (и/или r2) не в вакууме (воздухе), а в среде с показателем преломления n1 (n2), отличным от единицы, то геометрическую разность хода r необходимо заменять на оптическую. Оптический путь в n раз больше геометрического. Это связано с тем, что среда тормозит, замедляет световую волну в n раз по сравнению с вакуумом: = с/n. Поэтому тот же путь преодолевается с меньшей скоростью за большее время, что эквивалентно увеличению пути. Можно отметить также, что в среде уменьшается в n раз длина световой волны:
= Т = (с/n)Т = о/n, где о = сТ – длина световой волны в вакууме.
Интерференционную картину в естественном свете можно наблюдать, используя расщепление узкого пучка света, вырезанного из поля излучения одного и того же источника. Расщеплённые пучки, проходя разные пути и, накладываясь друг на друга, дают в области пересечения интерференционную картину. Ниже рассмотрены три примера интерференции в естественном свете: 1) опыт со щелями Юнга, 2) бипризма Френеля, 3) зеркало Ллойда.
О
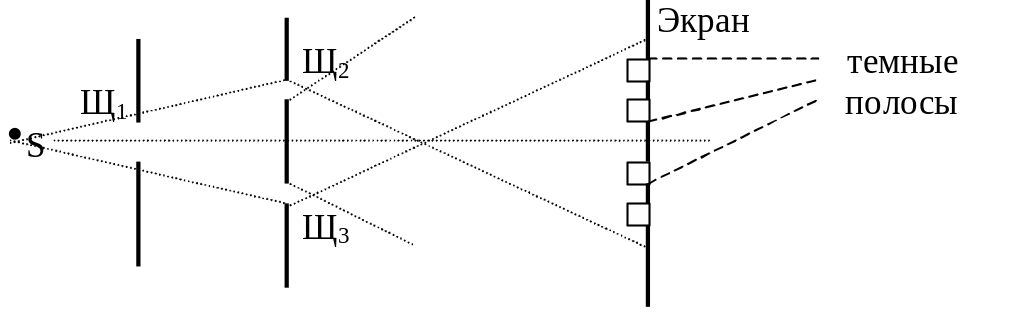
Опыт с бипризмой Френеля.
Расщепление узкого пучка света, падающего от источника S, осуществляется бипризмой - двумя призмами, склеенными своими основаниями. Каждая из призм, преломляя падающий на нее пучок света, отклоняет его к своему основанию. Поэтому за бипризмой оба пучка света пересекаются и на экране дадут интерференционную картину. Применительно к единой эквивалентной схеме роль двух точечных источников когерентного света здесь играют мнимые изображения S и S источника S, даваемые каждой из призм.
ДИФРАКЦИЯ СВЕТА.
Дифракция - близкое к интерференции и тесно взаимосвязанное с ней характерное волновое явление, наблюдаемое при рассеянии волн неоднородностями, соизмеримыми по величине с длиной волны света. Дифракция проявляется в проникновении (загибании) волн в область геометрической тени и образовании там интерференционной картины в виде чередующихся максимумов и минимумов интенсивности (освещенности). Неоднородности создают условия для пространственного наложения разных лучей из одного и того же светового пучка, которые, являясь когерентными, способны интерферировать.
Из общего случая дифракции, называемой дифракцией Френеля, выделяют частный, но важный случай, называемый дифракцией Фраунгогофера или дифракцией в параллельных лучах. Она имеет место, когда расстояния от неоднородности Н до источника света S и до экрана (на котором наблюдается интерференционная картина) много больше размера неоднородности.
О
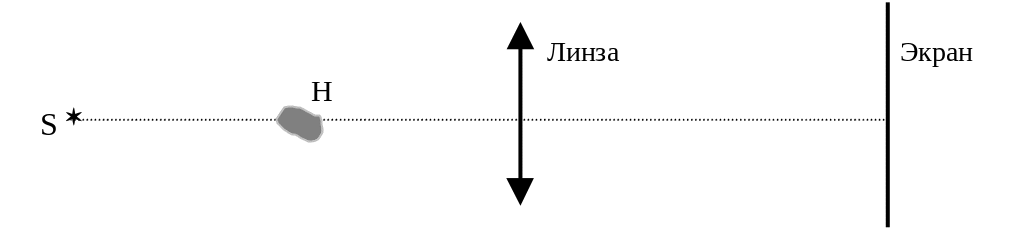
Основная задача теории дифракции - расчёт интенсивности (освещенности) в области за неоднородностями, препятствиями по заданному взаиморасположению источника света, неоднородности и экрана. Строгое решение этой задачи осуществляется путём решения (интегрирования) уравнений Максвелла с заданными граничными условиями - очень сложно. Но еще до открытия электромагнитной природы света, Гюйгенсом и особенно Френелем, были заложены основы упрощенного метода решения основной задачи теории дифракции.
Гюйгенс (1690 г) сформулировал принцип, согласно которому каждая точка волновой поверхности (до которой в данный момент дошла волна) становится элементарным (точечным) источником вторичных сферических волн, а огибающая этих вторичных волн даёт положение волнового фронта исходной волны в следующий момент времени.
Френель дополнил принцип Гюйгенса утверждением о когерентности вторичных волн и предложил далее решать задачу дифракции как результат интерференции вторичных волн. В результате объединённый принцип Гюйгенса-Френеля можно сформулировать так: реальный источник света в задачах дифракции можно заменять совокупностью элементарных когерентных вторичных источников света, распределённых по его волновой поверхности2 S.
Френель
предложил конкретный простой метод
выбора элементарных
источников, при
котором они выбираются в виде равновеликих
по площади полос (зон Френеля) волнового
фронта. При этом удаления от соседних
зон до точки наблюдения должны
отличаться на половину длины волны, то
есть разность хода волн, посылаемых
соседними зонами в точку наблюдения
равна /2,
а сами волны приходят в эту точку в
противофазе и ослабляют друг друга.
Поясним выбор этих зон на примере
точечного исходного источника,
излучающего сферические световые волны
(метод зон Френеля фактически позволяет
заменить интегрирование алгебраическим
суммированием).
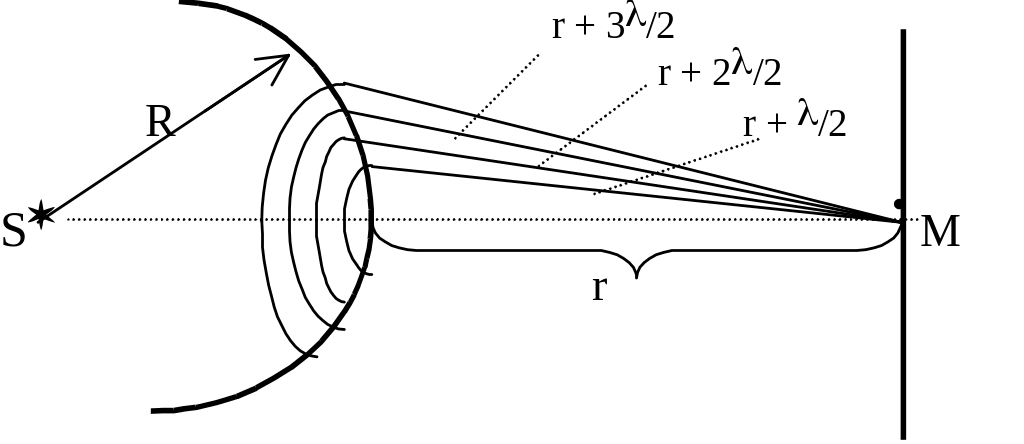
Размер (площадь) зоны Френеля подсчитывается по формуле: dS = Rr(R + r); при R = 1 м и r = 1 м, dS 1 мм2, то есть зоны Френеля очень малы.
Результирующая амплитуда А в точке М на экране определится суммой (алгебраической) амплитуд А1, А2, А3, … от элементарных вторичных источников - зон Френеля:
А = А1 –А2 + А3 – А4 + … Аk = А1 + (А1/2 – А2 + А3/2) + (А3/2 – А4 + А5/2) + … Аk/2 А1/2 Аk/2,
где знаки: плюс - для нечетного k и минус – для четного k (k – номер последней зоны Френеля).
Соседние зоны Френеля посылают свет в противофазе, и поэтому амплитуды посылаемых ими волн берутся с противоположными знаками. По причинам, изложенным выше, значение амплитуды монотонно убывает с ростом номера зоны Френеля: Am-1 Am Аm+1.
Д
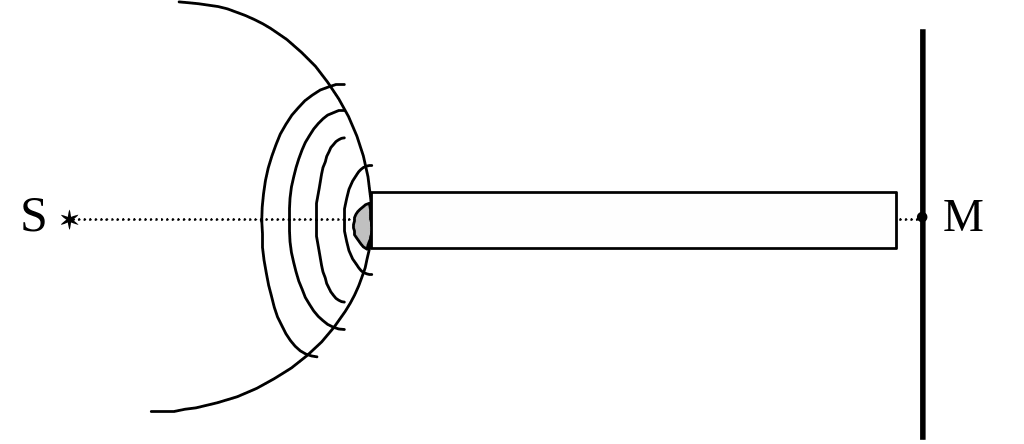
Дифракция Френеля на круглом отверстии и на непрозрачном диске.
Пусть между точечным источником света S и экраном Э расположена непрозрачная ширма с отверстием диаметром d. Для точки М на экране отверстие откроет некоторое число k зон Френеля. Тогда амплитуда результирующей волны в точке М определится выражением:
А = А1/2 Аk/2, где знак плюс - для нечетного k и минус – для четного k; k – номер последней открытой зоны.
Суть метода зон Френеля в том и заключается, что он интегрирование заменяет алгебраическим суммированием и фактически подсчётом числа зон Френеля; при этом важной оказывается степень чётности этого числа зон Френеля.
П
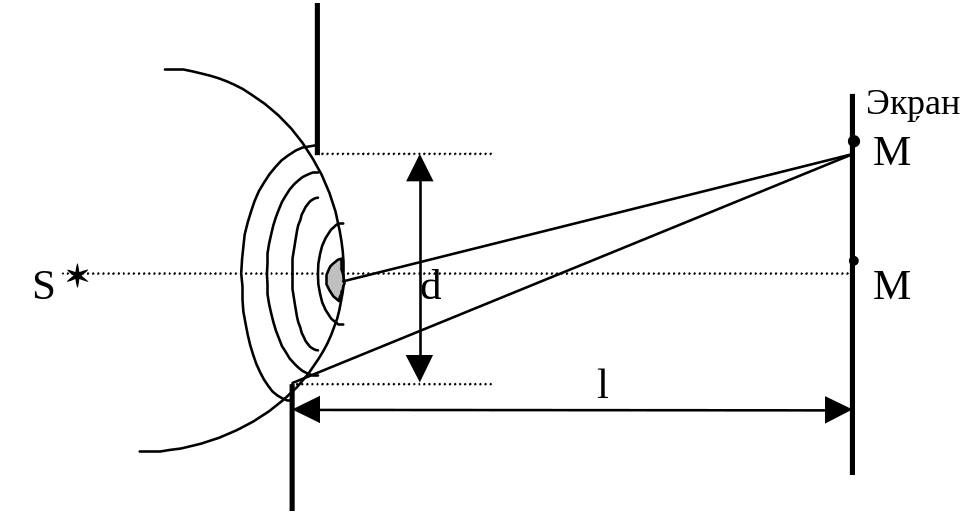
Если же число k зон Френеля будет чётным для точки М, в ней будет максимальная амплитуда: А = А1/2 + Аk/2. Здесь две половинки крайних нечётных зон Френеля оказываются нескомпенсированными и обусловливают максимум освещенности в точке М.
С перемещением точки М по экрану от центра число k зон Френеля, открываемых отверстием d для точки М будет изменяться. Соответственно при разных удалениях точки М от центра экрана будем наблюдать чередующиеся максимумы и минимумы освещенности, т. е. на экране будет иметь место интерференционная картина.
На примере дифракции света на круглом отверстии можно проиллюстрировать соотношение между геометрической и волновой оптиками и предельный переход волновой оптики в геометрическую при увеличении размеров неоднородности (здесь - отверстия) до значений много больших длины волны света. Действительно, если сделать отверстие довольно большого диаметра, то оно раскроет большое число k зон Френеля, так, что амплитуда последней открытой зоны Аk будет очень малой. И тогда разницы между максимумом Амакс = А1/2 + Аk/2 и минимумом Амин = А1/2 - Аk/2 практически не будет заметно. Соответственно, на экране исчезает интерференционная картина. Он весь освещен равномерно, как того и требует геометрическая оптика.
Рассмотрим
дифракцию Френеля на непрозрачном
диске диаметром d. Пусть он закрывает
для точки М на экране некоторое число
m зон Френеля.
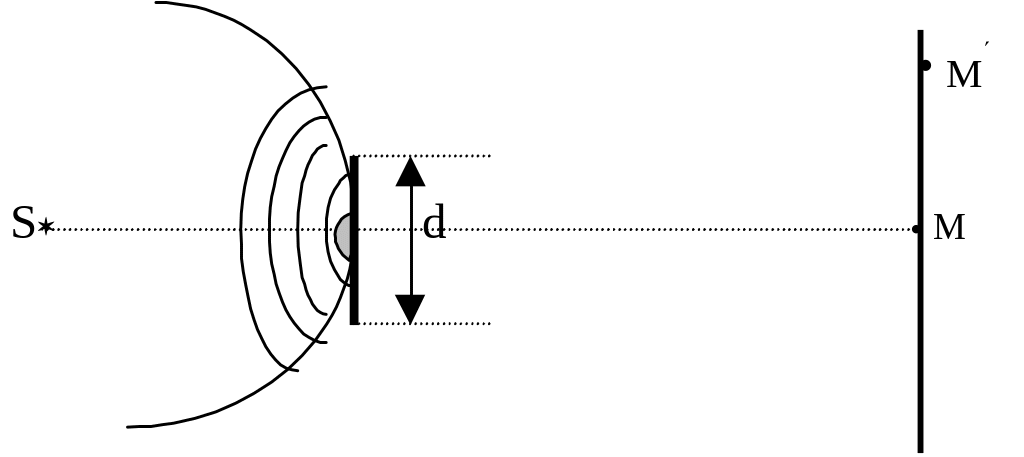
А = Аm+1/2 Аk/2 = Аm+1/2, так как Аk/2 0.
Интересно, что прямо против центра непрозрачного диска имеем светлое пятно, что противоречит положениям геометрической оптики, прямолинейности распространения света, образованию тени за непрозрачными препятствиями. В своё время этот парадокс (эффект Пуассона - Араго) был выдвинут французской академией наук в качестве одной из важнейших оптических проблем. Теоретически его обосновал Пуассон, а экспериментально проверил и подтвердил Араго.
При смещении точки М от центра по экрану число m зон Френеля, закрываемых диском для точки М, изменяется и, соответственно, изменяется освещенность экрана, т. е. максимумы сменяются минимумами, имеет место интерференционная картина.
На этом примере также можно проиллюстрировать предельный переход волновой оптики в геометрическую оптику. При увеличении размеров диска до значений, при которых он закрывает столь большое число зон Френеля, что первая открытая зона будет давать очень малую освещенность, всё поле пространства за экраном становится монотонно тёмным, превращаясь в обычную геометрическую тень. Лишь вблизи её границы будет наблюдаться слабая интерференционная картина. Таким образом, мы опять приходим к результату, что при d имеем дифракционное загибание света в область тени и образования там интерференционной картины, при другом же соотношении d , имеем прямолинейное распространение света и справедливость геометрической оптики.
Дифракция Фраунгофера на длинной и узкой щели
Р
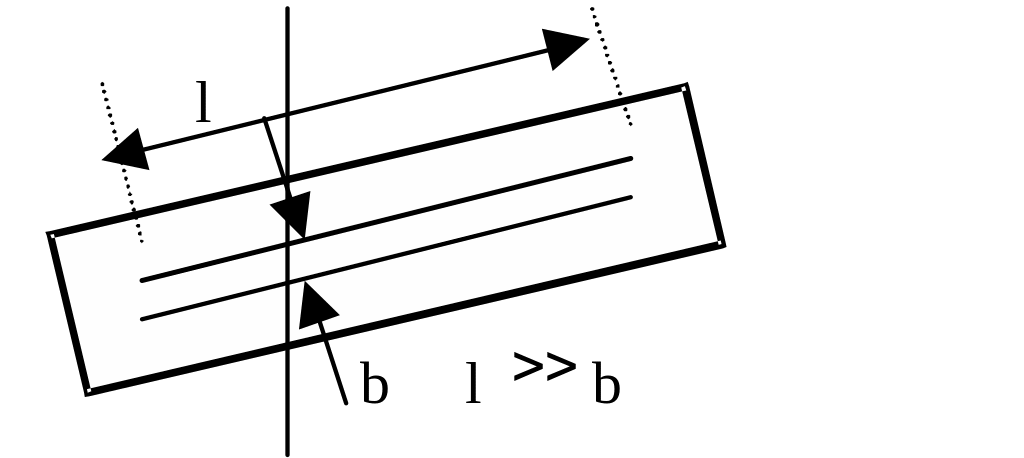
Пусть имеется длинная (l) и узкая шириной b щель в непрозрачном экране. Нормально к плоскости экрана падает пучок параллельных лучей (плоских волн).
З
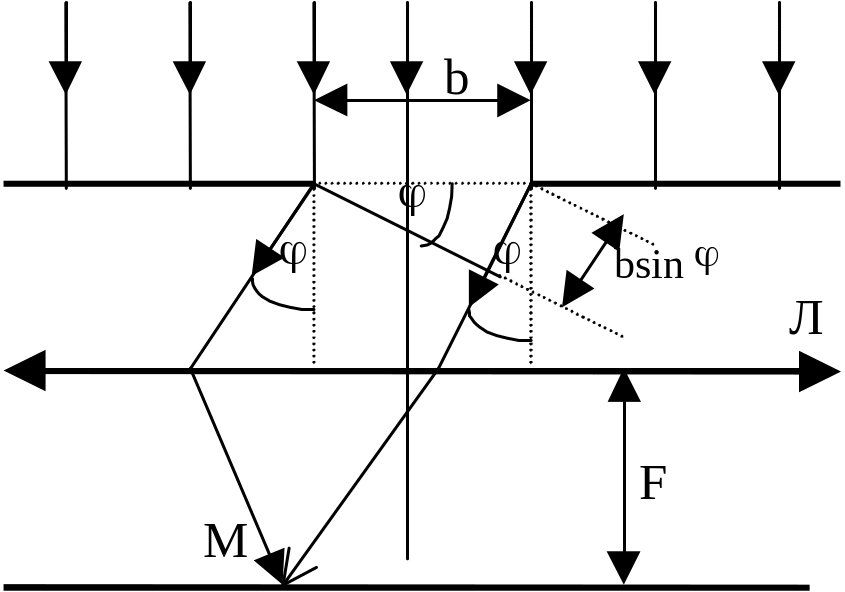
Разность хода для крайних лучей, рассеянных щелью под углом равна: = bsin . (Линза считается таутохронной - не вносящей дополнительной разности хода в проходящие через неё лучи). Так как соседним зонам Френеля соответствует разность хода в /2, то вся щель раскроет для точки М число k зон Френеля, равное: k = (/2) = bsin (/2) = 2bsin .
Чётному числу k зон Френеля соответствует условие минимума освещённости для соответствующего угла : 2bsin = 2m bsin = m -
- условие минимума, где m .
При m = 0 все зоны светят в одной фазе (разность хода посылаемых ими волн равна нулю) и максимально усиливают друг друга - имеем центральный максимум в дифракционном спектре.
При нечётном числе k зон Френеля имеем для соответствующего угла наблюдения максимум освещенности (боковые максимумы в дифракционном спектре): 2bsin = (2m + 1)
bsin = (m + ½) - условие максимума, где m - порядок дифракционного максимума.
О
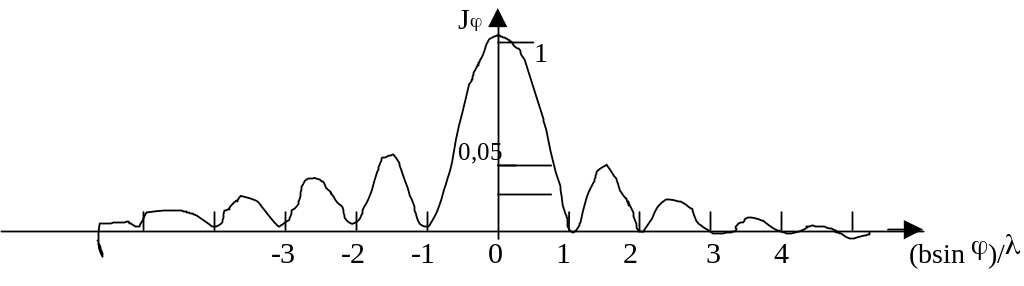
В белом свете центральный максимум остаётся белым, ибо его условие не зависит от значения длины волны. Боковые же максимумы для падающего на щель белого света окрашиваются и "разъезжаются" друг относительно друга тем сильнее, чем больше длина волны .
С увеличением длины волны угол , под которым наблюдается максимум m - го порядка увеличивается, т. к. большей соответствует большая необходимая разность хода , которая для своего обеспечения требует большего угла . Дифракционный спектр щели при этом растягивается, максимумы становятся шире и разносятся на большие углы.
С увеличением ширины щели b угол , под которым наблюдается максимум m - го порядка уменьшается, т. к. необходимая разность хода у более широкой щели достигается при меньшем угле отклонения . Дифракционный спектр при этом сжимается, максимумы становятся более узкими.
Дифракционная решетка, её спектр и характеристики.
Под дифракционной решеткой понимают спектральный оптический прибор, представляющий собой систему длинных и узких щелей или штрихов. Картина дифракции Фраунгофера на такой системе усложняется по сравнению с дифракционным спектром одной щели вследствие явления межщелевой интерференции света. Условие минимума для одной щели bsin = m сохраняется в качестве такового и для решётки в целом, ибо понятно, что если, под некоторым углом свет не посылает ни одна из щелей, то его под данным углом не посылает и решетка в целом. Условие же максимума для одной щели не может быть сохранено в качестве такового для решетки в целом, ибо, хотя каждая из щелей и посылает свет под некоторым углом, но в результате интерференции свет от отдельных щелей может гасить друг друга и давать в итоге минимум (свет плюс свет даёт тьму). Поэтому для более детального анализа картины дифракции Фраунгофера на решётке изобразим ход лучей, рассеянных ею под некоторым углом .
Максимумы,
называемые главными, будут наблюдаться
под такими углами, при которых соседние
щели светят синфазно, т. е. посылают
волны с разностью хода кратной целому
числу длин волн: dsin
= m
, где d - расстояние между соседними
щелями, называемое периодом или постоянной
дифракционной решётки, а m
- порядок главного максимума (порядок
спектра).
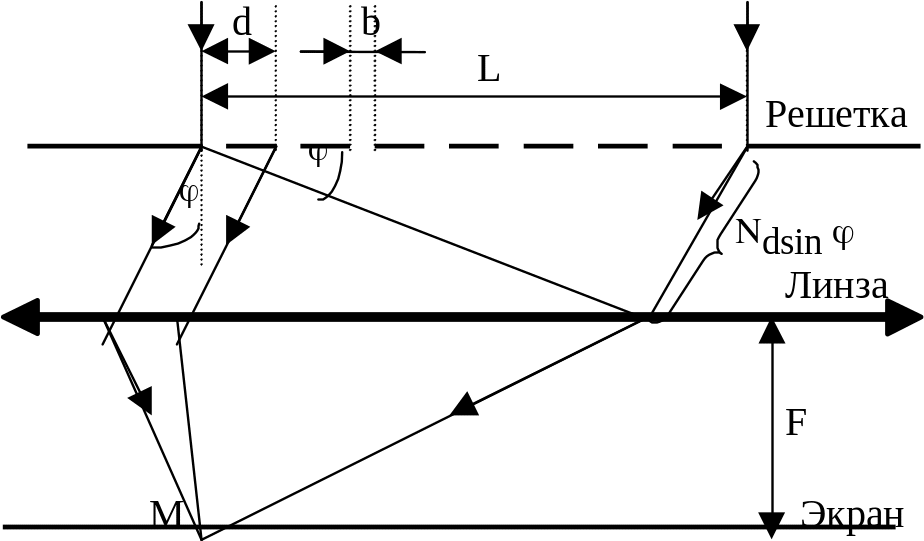
Главные максимумы в спектре дифракционной решётки воспроизводятся в виде узких световых полосок, называемых спектральными линиями.
Наложение межщелевой интерференции на картину дифракции от одной щели проявляется ещё и в появлении добавочных минимумов. Они наблюдаются под углами, соответствующими условию: dsin = р, где - полное число щелей в решётке и dsin - полная разность хода лучей, посылаемых краями (началом и концом) решётки под углом . Число р принимает целочисленные значения, исключая 0 и кратные числу щелей N в решётке, т. к. при этих значениях имеют место соответственно центральный и боковые главные максимумы.
При р = 1, dsin = р полная разность хода лучей посылаемых началом и концом решётки равна длине волны , значит первая половина щелей светит в противофазе второй половине и имеет место взаимопогашение, т. е. минимум (добавочный) в спектре решётки.
При р = 2 полная разность хода составляет 2. Здесь взаимно погашают друг друга волны света, посылаемые первой и второй четвертями всех щелей решётки, а также третей и четвёртой четвертями всех щелей, т. е. опять имеет место минимум.
П
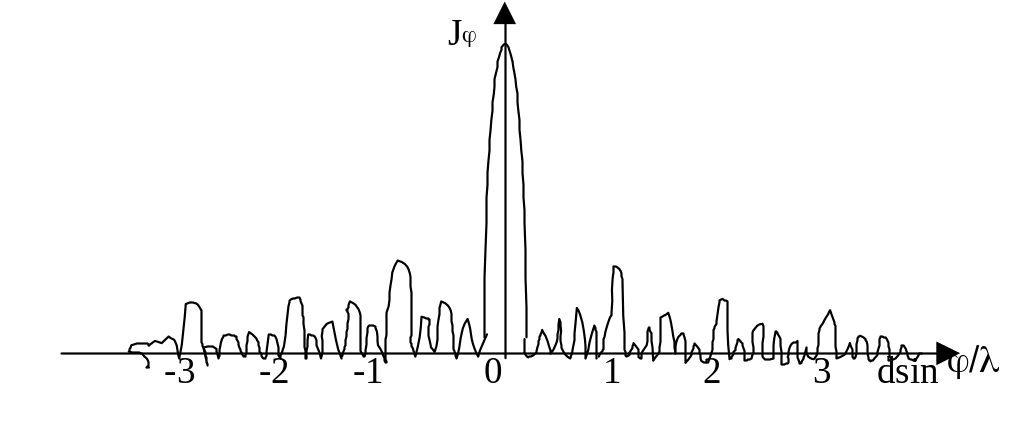
Между добавочными ми- нимумами размещаются доба- бавочные максимумы. В целом дифракционный спектр решётки будет иметь следующий вид:
Этот спектр, как и спектр отдельной щели, сим- метричен относительно центра- льного максимума, который несёт в себе основную интенсивность света соответствующей длины волны. Боковые максимумы быстро убывают по интенсивности с ростом их номера.
В белом свете центральный максимум остаётся белым, а боковые максимумы окрашиваются Волны с большими длинами отклоняются на большие углы. Это отличает дифракционный спектр от призменного, где сильнее отклоняются волны с большей частотой, т. е. с меньшей длиной волны.
ПОЛЯРИЗАЦИЯ СВЕТА
Представляя собой поперечные электромагнитные волны, свет обладает внутренней характеристикой (называемой поляризацией), отражающей возможность какого-либо упорядочения колебаний вектора (и, соответственно, вектора ) в плоскости перпендикулярной направлению распространения (вектору скорости ) волны.
Естественный свет является неполяризованным, в нем вектор с течением времени равновероятно и неупорядоченно занимает любые направления (в плоскости перпендикулярной вектору скорости волны).
В
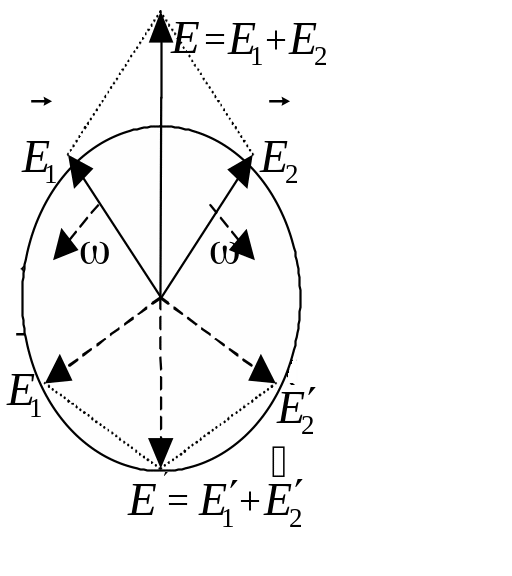
У
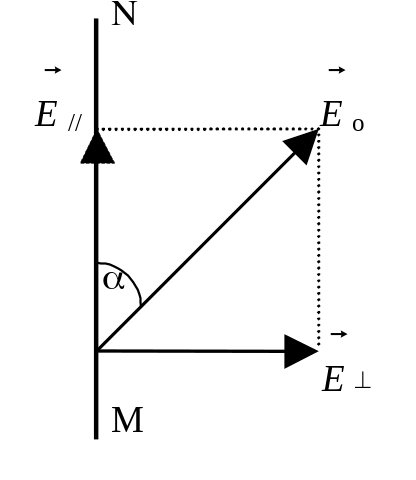
Если же на поляризатор падает линейно поляризованный свет (поляризатор в этом случае называют анализатором), то на выход проходит компонента Е//, параллельная плоскости анализатора М: Е// = Еоcos , гдe - угол между вектором о падающего на анализатор ЛПС и плоскостью анализатора. Интенсивность же ЛПС на выходе анализатора:
Jвых = Е//2 = Ео2cos2 = Jоcos2 .
Соотношение Jвых = Jоcos2 , связывающее интенсивности ЛПС на выходе и входе анализатора с углом между вектором о и плоскостью анализатора, называется законом Малюса.
Е
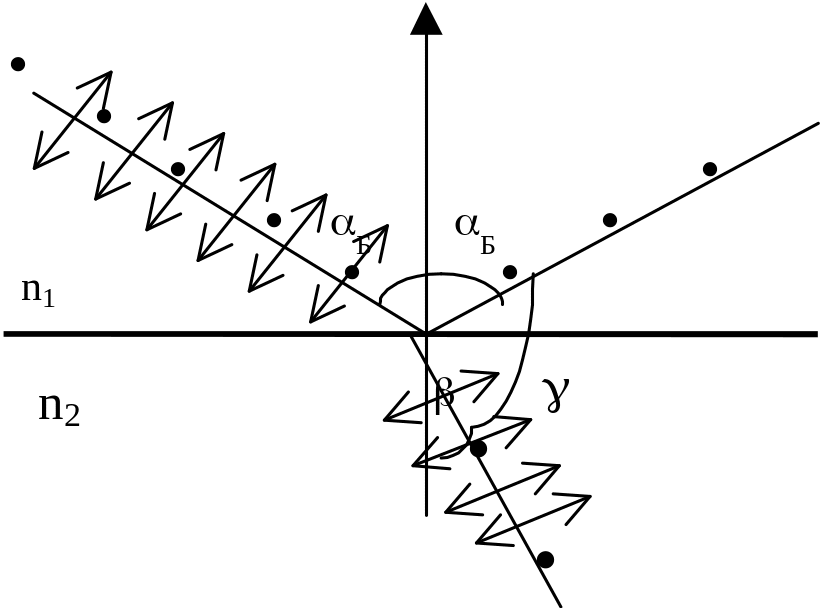
Если на границу раздела двух сред с показателями преломления n1 и n2, падает пучок естественного света под таким углом Б, при котором tg Б = n2n1, то, согласно закону Брюстера, отраженный луч оказывается полностью линейно поляризованным в плоскости перпендикулярной плоскости падения. Преломленный луч оказывается при этом частично (но наиболее) поляризованным, а угол между отраженным и преломленным лучами составляет 90°.
Перпендикулярность отраженного и преломленного лучей вытекает из формул закона Брюстера и закона преломления света:
t g
Б
= sin Бcos
Б
= n2n1
g
Б
= sin Бcos
Б
= n2n1
sin = cos Б + Б = 2
sin Бsin = n2n1 = - ( + Б) = /2
1 Белым называют обычный (естественный, видимый свет), включающий в себя «семь цветов радуги».
2 Волновой обычно называют поверхность, до которой в данный момент дошли колебания волны. Такую поверхность еще
называют фронтом волны. Она является эквифазовой поверхностью, то есть все ее точки колеблются в одинаковой фазе.
