Львівський державний університет безпеки життєдіяльності

МНС України

Кафедра фундаментальних дисциплін

Стасюк М.Ф., Карабин О.О.,

Меньшикова О.В., Трусевич О.М.

Методичні вказівки та завдання

до розрахункової роботи

з вищої математики

Елементи лінійної та векторної алгебри

та аналітичної геометрії

для студентів та курсантів I-го курсу

Львів 2007

Стасюк М.Ф., Карабин О.О., Меньшикова О.В., Трусевич О.М. Методичні вказівки та завдання до розрахункової роботи з вищої математики .Елементи лінійної та векторної алгебри та аналітичної геометрії. Для студентів та курсантів I-го курсу

Затверджено на засіданні кафедри фундаментальних дисциплін Львівського державного університету безпеки життєдіяльності МНС України. Протокол № ____ від “__” ____________ 2007 року.

 2007, Стасюк М.Ф., Карабин О.О., Меньшикова О.В., Трусевич О.М.

Важливим фактором в засвоєнні математики і оволодіння її методами є самостійна робота студента (курсанта). Система типових розрахунків активізує самостійну роботу студентів і сприяє більш глибокому вивченню курсу вищої математики. Застосування системи типових розрахунків рекомендовано програмою з вищої математики для вузів.

Даний методичний посібник містить теоретичні питання і розрахункову частину задачі. Теоретичні питання є спеціальними для всіх студентів, задачі для кожного студента групи індивідуальні (кожна задача складена в 31 варіанті).

Рекомендована література

1. А.Д.Кузик., О.М.Трусевич, О.О. Карабин. Аналітична геометрія. – ЛДУ БЖД.– 2006.– 101 с.

2. В. П. Дубовик, І. І. Юрик. Вища математика. – АСК. – К. 2001. – 647 С.

3. В. П. Дубовик, І. І. Юрик. Вища математика. Збірник задач – АСК. – К. 2001. – 479 С.

4. П. П. Овчинников, Ф.П. Яремчук, В. М. Михайленко. Вища математика. – Ч. 1, 2. – К. “Техніка”. – 2000.

Теоретичні питання

1. Матриці та дії над ними.

2. Визначники матриць, їх властивості.

3. Розв'язування систем лінійних рівнянь матричним способом і по правилу Крамера.

4. Вектори. Лінійні дії над векторами.

5. Скалярний добуток двох векторів, його властивості, застосування.

6. Векторний добуток двох векторів: означення, властивості, застосування,

7. Мішаний добуток трьох векторів: означення, властивості, застосування.

8. Площина. Векторна і координатна форми рівняння площини. Кут між двома площинами. Віддаль від точки до площини.

9. Пряма в просторі. Векторне, параметричне, канонічне рівняння прямої.

10. Основні задачі на пряму і площину.

Приклади розв’язання розрахункових завдань

Завдання №1. Розв’язати систему лінійних рівнянь:

(1)

а) методом Гауса;

б) методом Крамера;

в) матричним методом.

Розв’язання

а) Виконаємо елементарні перетворення над рядками розширеної матриці системи:

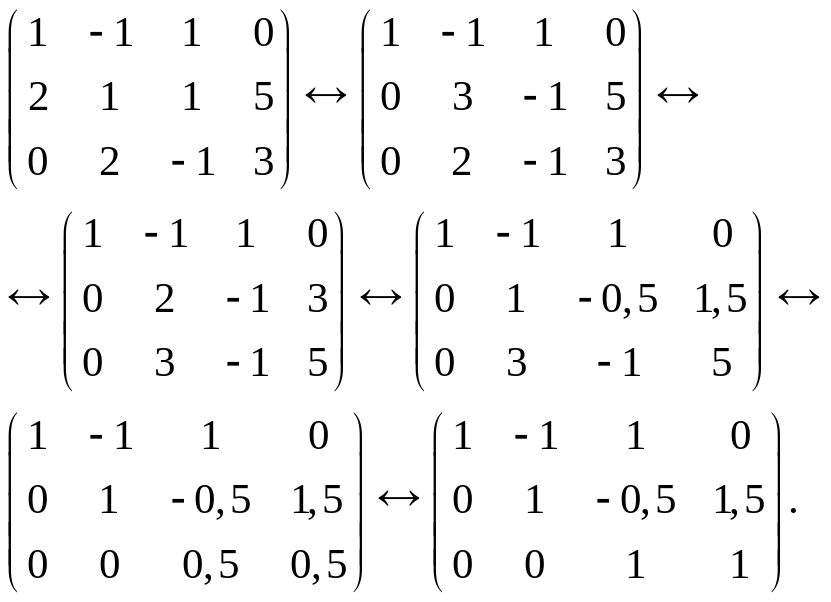
Ці перетворення не змінюють розв’язків системи (1), тобто є еквівалентними і позначаються символом « ». В даному прикладі їх можна описати в такий спосіб:

• перший рядок матриці залишаємо без змін;

• до другого рядка додаємо перший помножений на (-2);

• міняємо місцями другий і третій рядок;

• множимо другий рядок на 0,5;

• до третього рядка додаємо другий помножений на (-3);

• множимо третій рядок на 2.

За останньою розширеною матрицею складаємо еквівалентну до (1) систему рівнянь:

(2)

З системи (2) послідовно виключаємо невідомі: . Отже трійка чисел – єдиний розв’язок системи (2), а отже і (1).

Перевірка

Переконаємося, що розв’язок знайдений вірно, підставивши його в кожне з рівнянь системи (1). Отримаємо тотожності:

б) Обраховуємо послідовно головний та допоміжні визначники системи (1):

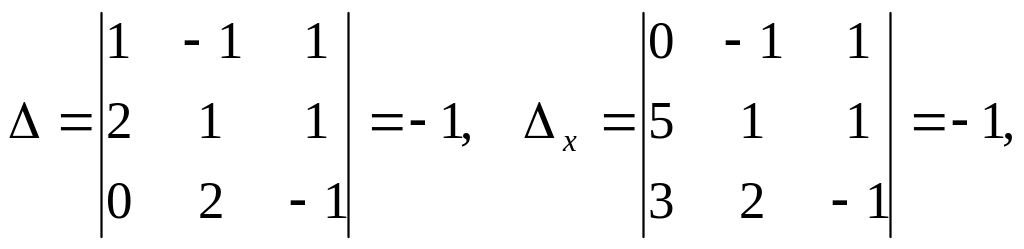
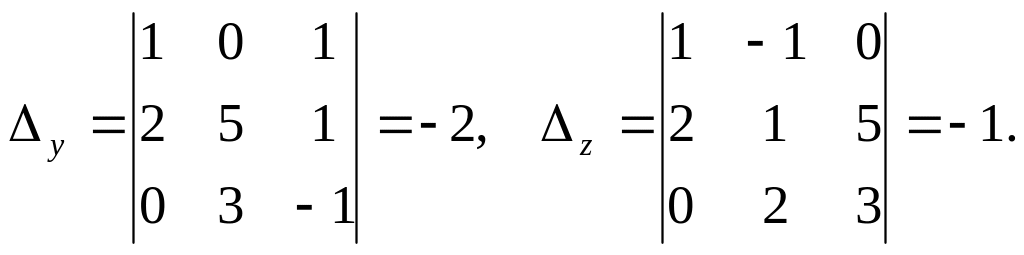
Тоді, за правилом Крамера, маємо:

Як бачимо, розв’язок отриманий методом Крамера, співпадає з попереднім, отриманим методом Гауса.

в) Запишемо систему (1) в матричній формі:

, (3)

де

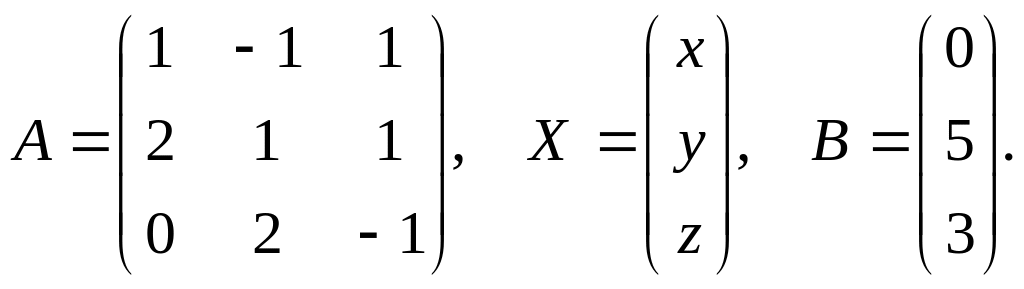
Оскільки – невироджена матриця , то існує обернена до неї матриця . Тоді, як відомо, єдиний розв’язок системи лінійних рівнянь (1) можна знайти у вигляді:

(4)

Шукаємо матрицю . Нагадаємо її структуру:

де – алгебраїчні доповнення до елементів матриці .

Далі маємо:

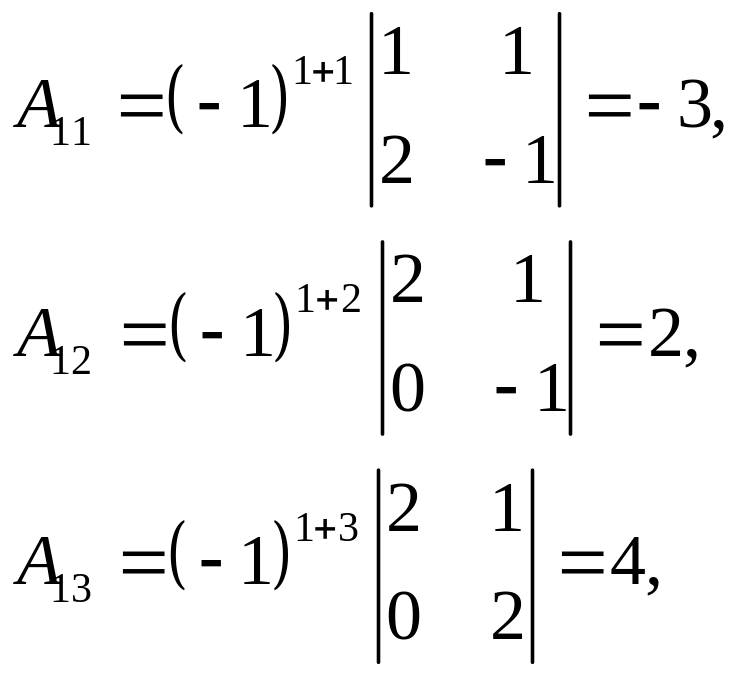
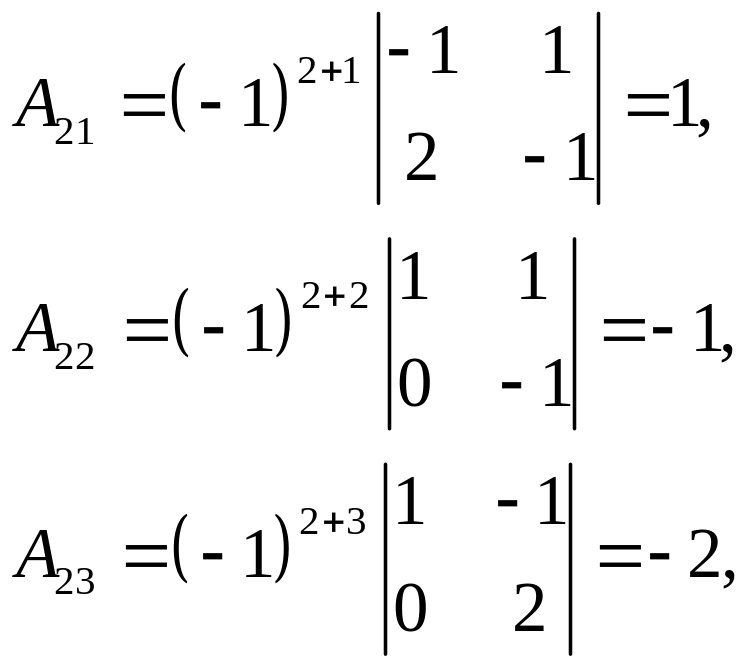
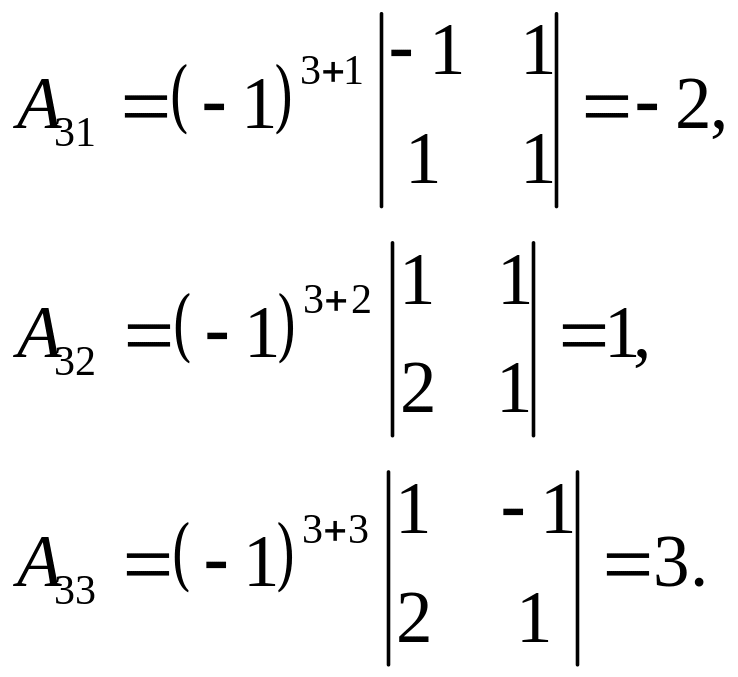
Тому

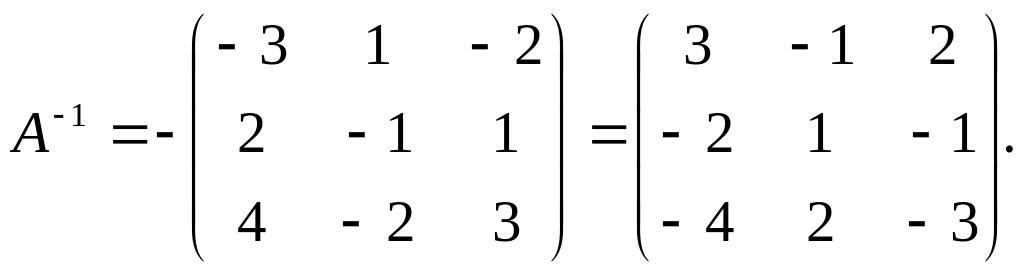
Отже за формулою (4) остаточно отримуємо:

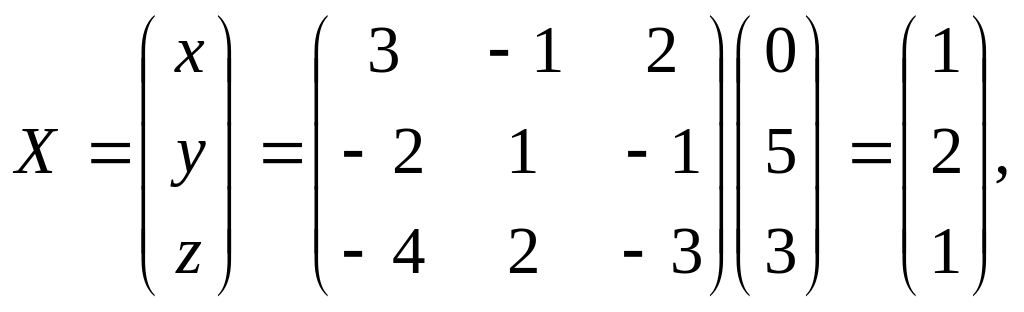
тобто трійка чисел: , як і в попередніх двох випадках, є розв’язком системи лінійних рівнянь (1).

Завдання №2. Задані точки: , Потрібно знайти:

а) кут між векторами і ;

б) площу паралелограма, побудованого на векторах і , де

в) з’ясувати лінійну залежність векторів де ;

г) знайти об’єм паралелепіпеда, побудованого на векторах де .

Розв’язання

а) Знайдемо спочатку вектори і за координатами їх початку і кінця:

Обчислимо довжини цих векторів:

і їх скалярний добуток:

З означення скалярного добутку векторів отримуємо:

де – кут між векторами і . Отже,

б) Площа паралелограма, побудованого на векторах і , обчислюється з допомогою векторного добутку

(5)

Знайдемо вектори

та векторний добуток в координатній формі

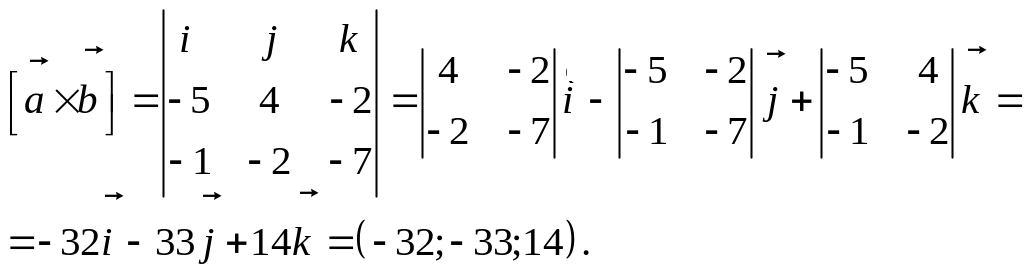
Обраховуючи довжину векторного добутку за формулою (5), маємо:

(кв. од.).

в) Знайдемо вектор де Як і в попередній задачі, маємо

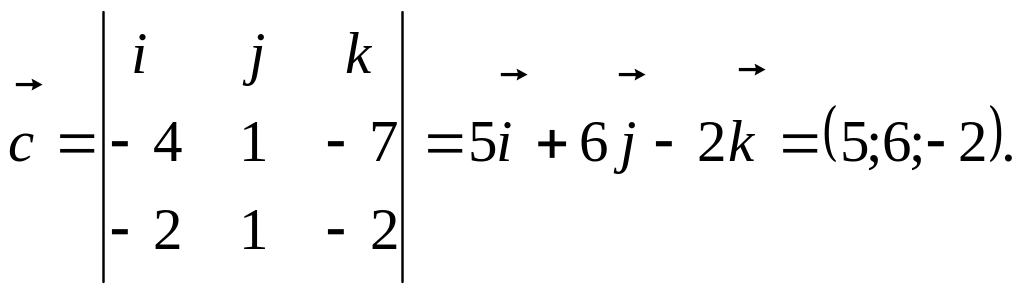
Обчислимо мішаний добуток векторів і в координатній формі:

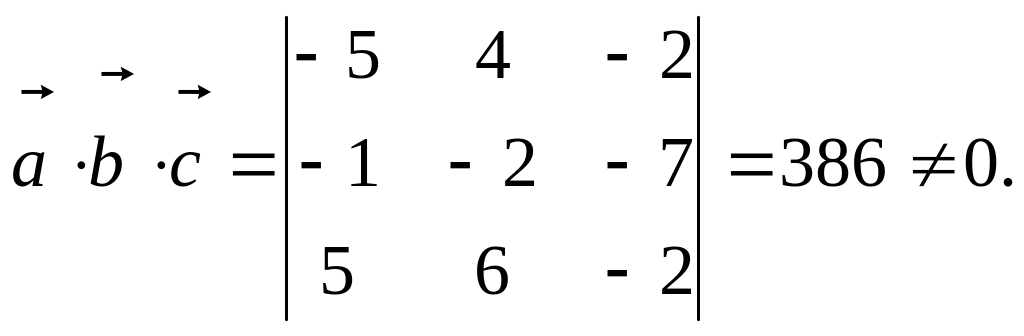
Отже, вектори – некомпланарні, тобто лінійно незалежні.

г) Як відомо, об’єм паралелепіпеда, побудованого на векторах і , обчислюється за допомогою мішаного добутку векторів, а саме:

. (6)

Обчислимо цей добуток:

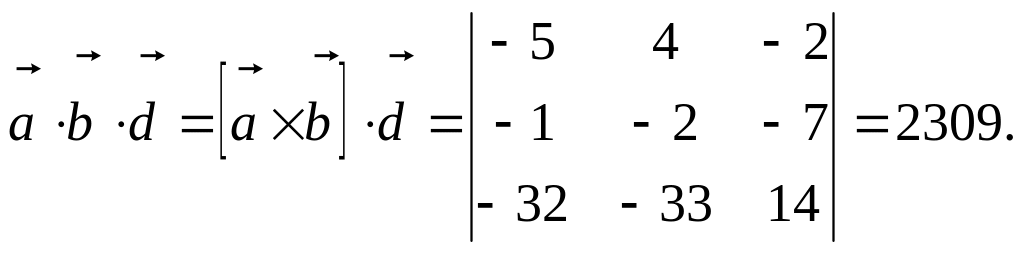
Тому за формулою (6) маємо

(куб. од).

Об’єм цього паралелепіпеда можна знайти й іншим шляхом, якщо зауважити, що вектор . Тоді

(скалярний квадрат був порахований в задачі 2б)).

Завдання №3.. Задано точки : , . Написати:

а) канонічне рівняння прямої, що проходить через точку паралельно до вектора

б) рівняння площини , що проходить через точку , перпендикулярно до вектора

в) рівняння площини , що проходить через точки ;

г) знайти кут між площинами і ;

д) якщо , записати канонічне рівняння прямої, що утворюється в результаті перетину площин і .

Розв’язання

а) Канонічне рівняння прямої, що проходить через точку паралельно до вектора має вигляд:

Оскільки і то шукане рівняння запишеться так:

б) Запишемо рівняння площини , використовуючи рівність нулю скалярного добутку взаємно перпендикулярних векторів і , де – біжуча точка площини . Далі маємо:

Тоді отримуємо:

Отже, – загальне рівняння площини .

в) Рівняння площини , що проходить через точки як відомо, має вигляд:

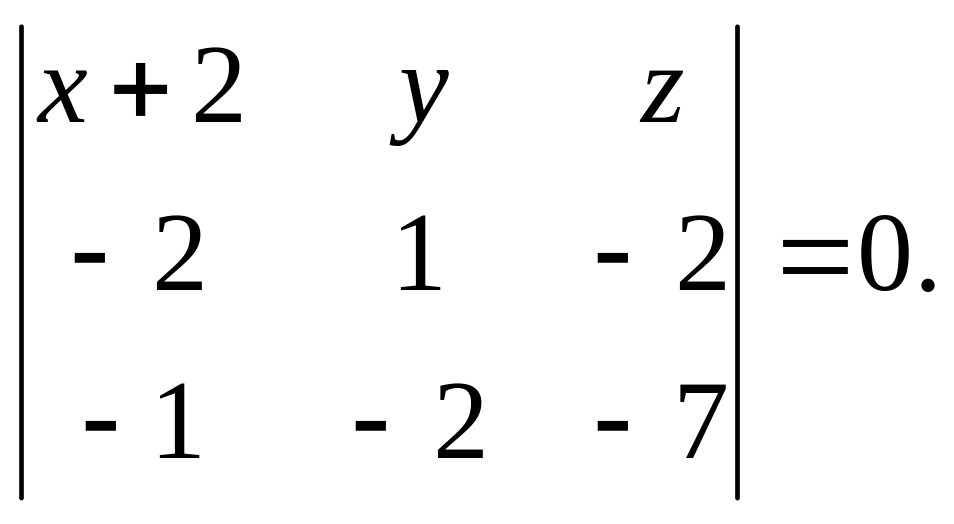(7)

Зауважимо, що рядками визначника (7) є координати векторів відповідно, де – біжуча точка площини . Розкривши визначник в лівій частині рівності (7) за елементами першого рядка, прийдемо до загального рівняння площини :

або остаточно

г) Кут між площинами і – це кут між нормальними векторами і цих площин. Знайдемо ці вектори:

Використовуючи скалярний добуток векторів і , отримуємо:

тобто і площини , – взаємно перпендикулярні.

д) Щоб записати канонічне рівняння лінії перетину площин і потрібно знайти:

• напрямний вектор 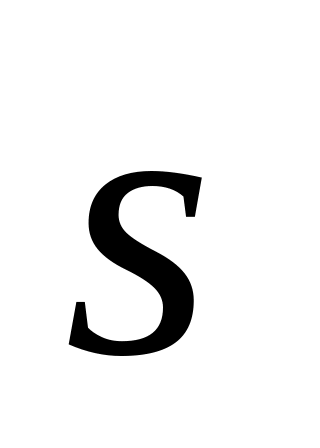прямої ;

• яку-небудь точку перетину цих площин (прямої ).

За напрямний вектор можна взяти векторний добуток векторів і (див. пункт г)). Знайдемо вектор в координатній формі:

.

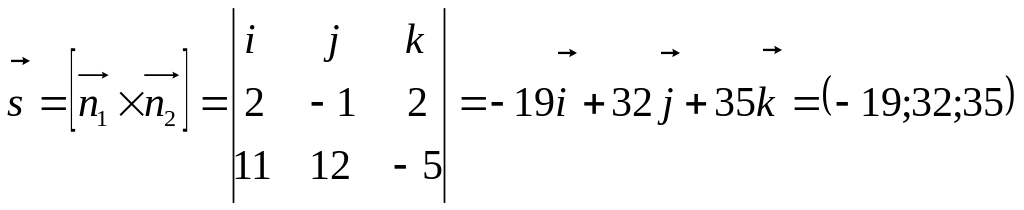Спільною точкою площин і є, наприклад, точка .

Тому канонічним рівнянням прямої (див. задачу 3а)) є наступне рівняння: