4.4.2 Критерий устойчивости Гурвица

При использовании этого критерия из коэффициентов характеристического уравнения системы составляют таблицу

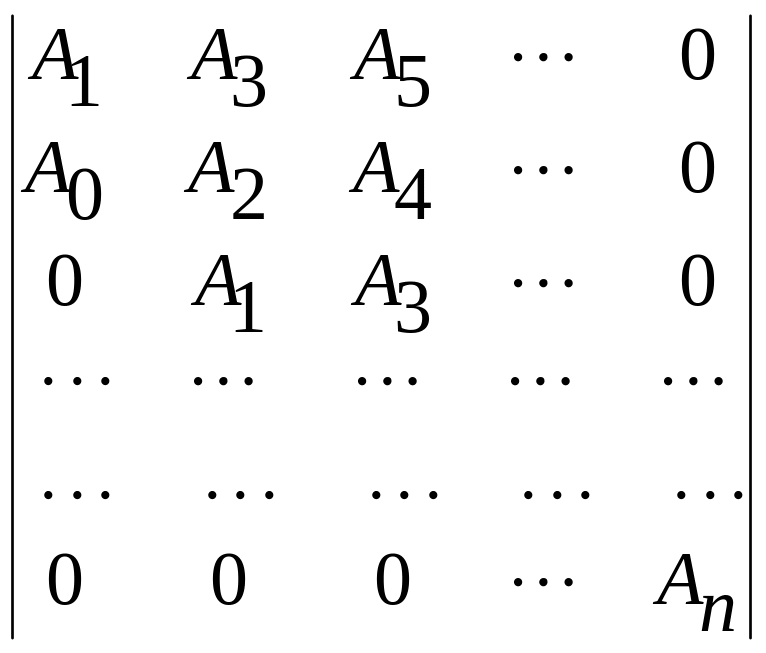
По диагонали таблицы от левого верхнего угла выписывают по порядку все коэффициенты, начиная с и заканчивая . Затем каждый столбец таблицы дополняют так, чтобы вверх от диаго­нали индексы коэффициентов увеличивались, а вниз — умень­шались. В случае отсутствия в уравнении какого-либо коэффи­циента и вместо коэффициентов с индексом меньше 0 и больше n пишут нуль.

Критерий можно сформулировать так: система устойчива, если при > 0 положительны и п диагональных миноров Гурвица, т.е.

; ; ; ; .

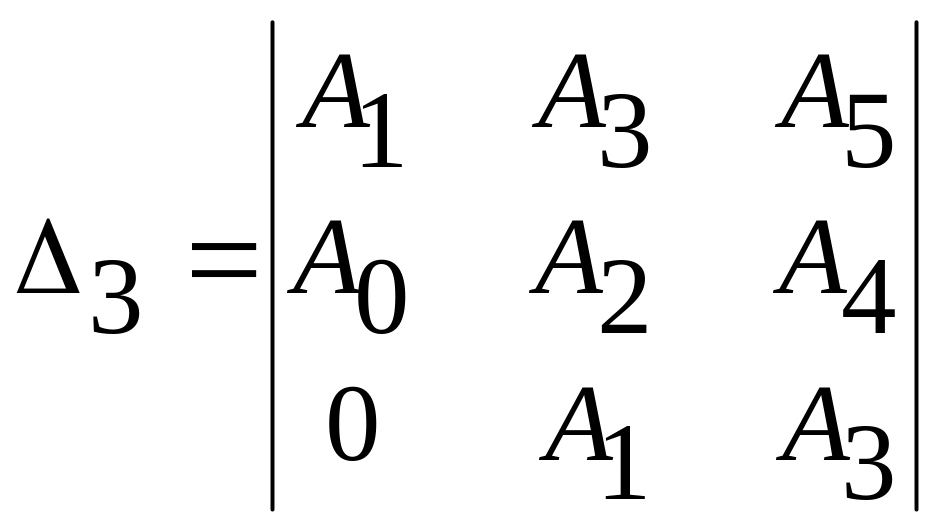Это необходимое и достаточное условие устойчивости.

Предпоследнее неравенство есть , поэтому по­следнее неравенство сводится к > 0.

Система находится на границе устойчивости, если и все предыдущие определители Гурвица положительны. Условие распадается на два: = 0 (апериодическая граница устойчивости, нейтральная устойчивость) или (колебательная граница устойчивости).

Раскрывая, например, определители Гурвица для характеристических уравнений третьего, четвертого и пятого порядков, можно получить следующие условия устойчивости:

для системы третьего порядка

, , , , ;

для системы четвертого порядка

, , , , , ;

для системы пятого порядка

, , , , , ;

;

.

Используя критерий Гурвица, можно при заданных параметрах системы принять за неизвестный один какой-либо параметр и определить его предельное значение, при котором система будет находиться на границе устойчивости.

В случае применения критериев Рауса и Гурвица о запасе устойчивости можно судить по тому запасу, с которым выполняются входящие в эти критерии неравенства.

4.5 Устойчивость сау по критерию Михайлова

Критерий Михайлова: для устойчивости системы порядка необходимо и достаточно, чтобы годограф Михайлова начинался на вещественной положительной полуоси и охватывал в положительном направлении (против часовой стрелки) квадрантов ( степень характеристического уравнения), все время охватывая начало координат и нигде не обращаясь в нуль.

Для критерия Михайлова необходим характеристический полином, получаемый из знаменателя передаточной функции замкнутой системы.

.

Если заменить в этом полиноме оператор Лапласа на мнимое значение , то получим комплексный полином

;

.

Годограф Михайлова есть кривая, которую описывает конец вектора на комплексной плоскости при изменении от 0 до . Для систем порядка примерный вид годографа Михайлова приводится на рис.4.

Иногда удобнее пользоваться другой формулировкой критерия Михайлова: для устойчивости замкнутой системы необходимо и достаточно, чтобы корни мнимой (полином V()) и действительной (полином U()) частей её характеристического вектора были вещественными положительными и чередовались (удобнее пользоваться выражениями для квадратов корней), т.е. выполнялись неравенства

где , - корни полинома U(); , - корни полинома V().

У неустойчивых систем годографы Михайлова имеют разнообразную форму.

На рис.5 показаны годографы неустойчивых систем четвёртого порядка. Их характеристический полином имеет положительный вещественный корень (кривая 1), два положительных вещественных корня (кривая 2), два комплексно- сопряженных корня с положительной вещественной частью (кривая 3), два чисто мнимых корня и положительный вещественный (кривая 4).

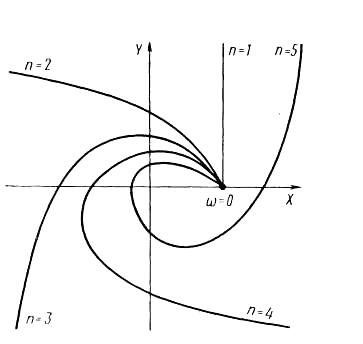
Рис.4. Годографы Михайлова устойчивых систем при различном порядке характеристического вектора

При использовании критерия Михайлова о запасе устойчивости САУ можно судить по степени удалённости годографа от начала координат.

4.6 Устойчивость САУ по амплитудно-фазовой частотной и логарифмическим характеристикам

4.6.1 Частотный критерий Найквиста

Частотный критерий Найквиста дает возможность определить устойчивость замкнутой САУ по амплитудно-фазовой частотной характеристике W_P(j) ее разомкнутой цепи, если удовлетво­ряется условие

lim|W_P(j) | =С. (*)



При этом под термином "замкнутая САУ" понимается САУ, приведенная к одному динамическому звену с передаточной функцией W_P(s) в прямой цепи, охваченному единичной отрицательной обратной связью (рис.6).

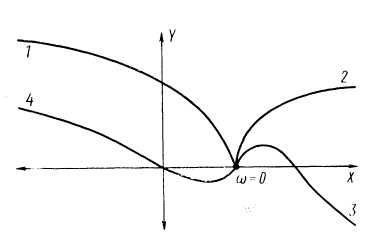
Рис. 5. Годографы Михайлова неус­тойчивых систем четвертого порядка

Для удовлетворения условия (*) степень m числителя передаточной функции W_P(j) разомкнутой системы не должна быть выше степени n ее знаменателя, что выполняется для любых реальных систем.

X (s) W_P(s) Y (s)

Рис. 6.

На первом этапе необходимо определить устойчивость иссле­дуемой системы в разомкнутом состоянии. В одноконтурной системе, составленной из последовательно соединенных звеньев, корни характеристических полиномов этих звеньев являются одновременно корнями характеристического полинома разомкнутой системы.

Различают три случая применения критерия Найквиста.

a) разомкнутая система устойчивая. В этом случае для устой­чивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении  от 0 до  не охватывала точку с координатами [-1; j0].

На рис.7 изображены возможные ситуации. При АФЧХ, показанной кривой 1, замкнутая система абсолютно устойчива, т. е. она остаётся устойчива и при уменьшении передаточного коэффициента разомкнутой цепи. Если АФЧХ является кривая 2, то замкнутая система условно устойчива. Она остается устойчи­вой только при значении k, лежащем в некоторых пределах. Кри­вая 3 проходит через критическую точку с координатами [-1; j0]. Это означает, что замкнутая система находится на колебатель­ной границе устойчивости. Кривая 4 охватывает критическую точку, поэтому замкнутая система неустойчивая.

Для неустойчивой разомкнутой системы нужно выяснить, какое число корней k ее характеристического полинома имеет положительные веществен­ные части.

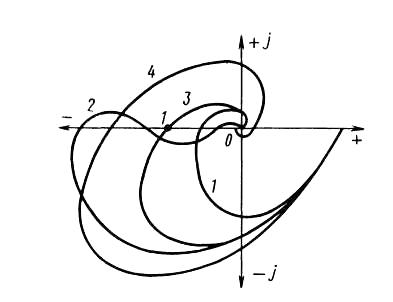
Рис. 7. Амплитудно-фазовые частотные характеристики устойчивых

разомкнутых систем

б) разомкнутая система на границе устойчивости. Характеристический полином такой разомкнутой САУ имеет нулевые или чисто мнимые корни, а у остальных корней отрицательные вещественные части. В обоих случаях для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ при изменении  от 0 до , дополненная на участке разрыва дугой бесконечного радиуса (по часовой стрелке), не охватывала точку с координатами [-1; j0].

в) разомкнутая система не устойчивая. Характеристический полином такой САУ имеет k корней с положительной вещественной частью. В этом, наиболее общем, случае критерий Найквиста форму­лируют так: для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении  от 0 до  вектор, начало ко­торого находится в точке с координатами [-1; j0], а конец на АФЧХ разомкнутой си­стемы, повернулся в положительном направлении (против часо­вой стрелки) на угол k• 180°.

При сложной форме АФЧХ разомкнутой системы удобнее при­менять другую формулировку критерия Найквиста, которая ис­пользует правило переходов. Переход АФЧХ при увеличении  через отрезок вещественной оси от -1 до  сверху вниз считают положительным и снизу вверх отрицательным (рис.8). АФЧХ может начинаться на указанном отрезке при  = 0 или заканчи­ваться при  = . Тогда считается, что она совершает полпере­хода.

Критерий формулируют так: замкнутая система устойчива, если разность между числом положительных и отрицательных переходов амплитудно-фазовой частотной характеристики разом­кнутой системы через отрезок вещественной оси от -1 до -  равен k/2. Здесь k — число корней характеристического полинома разомкнутой системы с положительной частью.

При наличии у характеристического полинома нулевых и чисто мнимых корней АФЧХ на участках разрыва должна быть дополнена дугой бесконечно большого радиуса.

Для применения критерия Найквиста исследуемая система может быть разомкнута в любой точке, т.е. может быть разомкнута не главная обратная связь, а одна из местных обратных связей.

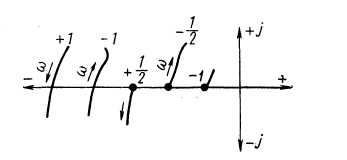
Рис.8. Обозначение знака пе­рехода АФЧХ через отрезок веще­ственной оси от - 1 до - 

При использовании критерия устойчивости Найквиста по АФЧХ о запасе устойчивости САУ можно судить по степени удалённости годографа W_P(j) от точки с координатами [-1; j0].

4.6.2 Логарифмический критерий устойчивости Найквиста. Основное удобство применения критерия устойчивости Найквиста заключается в том, что он легко переносится на логарифмические частотные характеристики разомкнутой системы, которые, в свою очередь, могут быть легко построены, особенно в том случае, если разомкнутая САУ представляется в виде совокупности последовательно соединенных типовых динамических звеньев.

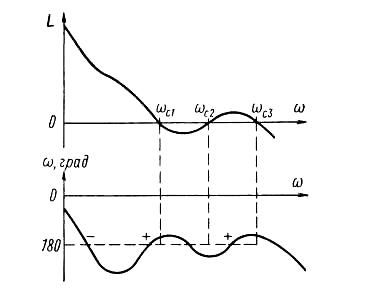
Рис. 9. Логарифмические частотные характеристики неустойчивой

(k= 2) ра­зомкнутой системы

Применительно к ЛАФЧХ критерий может быть сформирован так: для устойчивости замкнутой САУ необходимо и достаточно, чтобы при положительных значениях ЛАХ (L()>0) разность между числом положительных и отрицательных переходов ФЧХ через линии -180⁰; 3180⁰… равнялась k/2, где k - число корней с положительной вещественной частью характеристического полинома разомкнутой САУ. Пересечение ФЧХ линий -180; 3180… снизу вверх считается положительным переходом, а сверху вниз - отрицательным.

Из анализа графиков рис.9 видно, что разность между положительными и отрицательными переходами ЛФХ через -180⁰ при L()>0 равна +1. Таким образом, если знаменатель передаточной функции W_P(s) имел 2 “плохих” корня (k=2), то замкнутая система будет устойчива.

Типичные логарифмические характеристики разомкнутой САУ приведены на рис.10.

4.7 Определение запаса устойчивости по ЛАФЧХ

Основное распространение в качестве меры запаса устойчивости получили две величины – запас устойчивости по амплитуде L и запас устойчивости по фазе .

Запас устойчивости по амплитуде определяется величиной L допустимого подъёма ЛАХ, при котором система окажется на границе устойчивости.

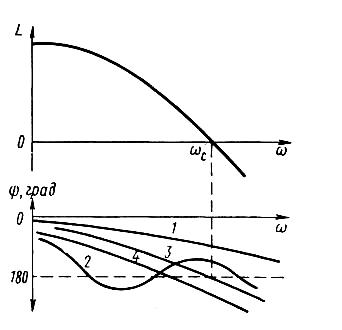
Рис. 10. Логарифмические частотные характеристики разомкнутой САУ:

1- замкнутая САУ абсолютно устойчива; 2- условно устойчива;

3 – на границе устойчивости; 4 – неустойчива

Запас устойчивости по фазе определяется величиной , на которую должно возрасти запаздывание по фазе в системе на частоте _С, чтобы система оказалась на границе устойчивости.

Таким образом, в случае использования ЛАФЧХ запас устойчивости по амплитуде оп­ределяется в точке пересечения ЛФХ прямой -180⁰, а запас устойчивос­ти по фазе - в точке пересечения ЛАХ оси абсцисс. Эти величины показаны на рис.11.

При практическом проектировании САУ рекомендуется назначать запас устойчивости по амплитуде L > 6 дБ (это соответствует примерно двойному запасу коэффициента передачи), а по фазе  > 30°.

Метод исследования устойчивости с помощью логарифмических частотных характеристик получил широкое распространение в инженер­ной практике из-за простоты построения и наглядности ЛАХ и ЛФХ. ЛАХ разомкнутой САУ применяется не только для ана­лиза устойчивости, но и дает много другой информации о свойствах системы и часто используется при синтезе САУ.

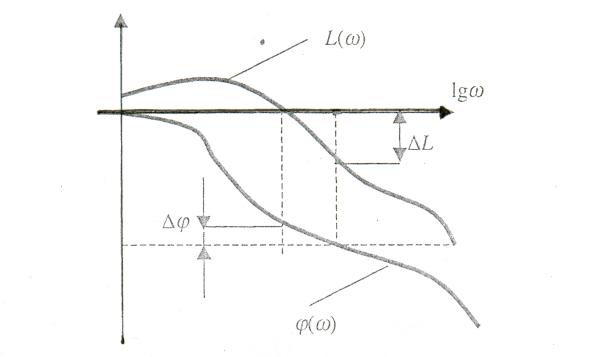
Рис. 11. Определение устойчивости по логарифмическому критерию Найквиста

Все рассмотренные критерии равноценны для определения факта ус­тойчивости САУ. В некоторых случаях алгебраические критерии позволяют получить аналитические выражения для оценки устойчивос­ти, накладывающие ограничения на параметры системы, которые напря­мую связаны с коэффициентами характеристического уравнения. Однако эти методы применимы в случаях, когда известно аналитичес­кое выражение дня коэффициентов характеристического уравнения.

Частотные критерии позволя­ют, помимо прочего, достаточно просто определить "физические" ха­рактеристики системы (полосу пропускания, резонансные частоты и т.п.). Они требуют большего времени на анализ устойчивости по сравнению с алгебраическими методами и связаны с графическими пост­роениями. Достоинством частотных критериев является то, что при отсутствии аналитического описания САУ они по­зволяют определить устойчивость по экспериментально снятым частотным характеристикам.

ЛИТЕРАТУРА

1. Теория автоматического управления: учебник для вузов. В 2-х ч. Ч.1: Теория линейных систем автоматического управле­ния/ Н.А. Бабаков, А.А. Воронов [и др.]; под ред. А.А.Воронова. - М.: Высш. шк.,1986. - 367 с.

2. Теория автоматического управления: учебник для вузов. В 2-х ч. Ч.2: Теория нелинейных и специальных систем автома­тического управления/ А.А. Воронов, Д.П. Ким, В.М. Лохин [и др.]; под ред. А.А. Воронова. - М.: Высш. шк.,1986. - 504 с.

3. Попов, Е.П. Теория линейных систем автоматического регулирования и управления./ Е.П. Попов. - М.: Наука, 1978. -256 с.

4. Попов, Е.П. Теория нелинейных систем автоматического регулирования и управления./ Е.П. Попов. - М.: Наука, 1979. -256 с.

5. Макаров, И.М. Линейные автоматические системы/ И.М. Макаров, Б.М. Менский. - М.: Наука, 1977. - 312 c.

6. Куропаткин, П.В. Теория автоматического управления/ П.В. Куропаткин. - М.: Высшая школа, 1973. - 410 с.

7. Бесекерский, В.А. Теория систем автоматического регулирования/ В.А. Бесекерский, Е.П. Попов. - М.: Высш. шк., 1972. - 860 с.

8. Солодовников, В.В. Основы теории и элементы систем автоматического регулирования/В.В. Солодовников, В.Н Плотников, А.В. Яковлев. - М.: Машиностроение, 1985. - 536 с.

9. Основы теории автоматического регулирования: учебн. для машиностр. спец. вузов/ В.И. Крутов, Ф.М. Данилов, П.К. Кузьмик [и др.]; под ред. В.И. Крутова.- М.: Машиностроение,1984. -368 с.

10. Теория автоматического управления: учебник для вузов по специальностям «Технология машиностроения» и «Металлорежущие станки и инструменты» / В.Н. Брюханов, М.Г. Косов, С.П. Протопович [и др.]; под ред. Ю.М. Соломенцева. – М.: Машиностроение, 1992. – 172 с.

11.Андриевский, Б.Р. Избранные главы теории автоматического управления с примерами на языке MATLAB/ Б.Р. Андриевский, А.Л. Фрадков. – СПб.: Наука, 1999. – 467 c., ил.85 (Серия “Анализ и синтез нелинейных систем”)