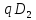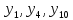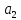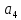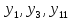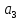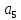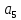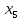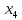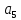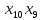ВМИС 30 вариант

Задание 1.1. Найти значений С1, С2, С3, С4, определяемые выражениями: С1 = А+В, С2 = А-В, С3 = В- А+, С4 =- А -В, где, согласно варианту, А=-1184, В=-477. При выполнении вычислении использовать двоично-десятичный обратный код.

Решение

Представим числа A, -A, B, -B в обратном коде. Если число отрицательное в знаковый разряд минус, все остальные разряды инвертируются. Если число положительное в знаковые разряд ноль, остальные такие же, как в прямом коде.

- 1 1 8 4

[A]_пк(-1184)=1.0001 0001 1000 0100

[А]_ок =1.1110 1110 0111 1011

+ 1 1 8 4

[-A]_пк(1184)=0.0001 0001 1000 0100

[-А]_ок = 0.0001 0001 1000 0100

- 0 4 7 7

[B]_пк(-0477)=1.0000 0100 0111 0111

[B]_ок =1.1111 1011 1000 1000

+ 0 4 7 7

[-B]_пк(0477)=0. 0000 0100 0111 0111

[-B]_ок =0. 0000 0100 0111 0111

C1=A+B=-1184-477=-1661

* * * *

1.1110 1110 0111 1011 [A]ок

1.1111 1011 1000 1000 [В]ок

11.1110 1010 0001 0011 +1

1.1110 1010 0001 0100

1. 0001 0101 1110 1011 преобразуем в прямой код, далее коррекция

0000 0000 0110 0110 если в тетраде запрещенная комбинация прибавляем 6,

перенос учитываем в следующей тетраде

1. 0001 0110 0110 0001 - [C1]_ПК

- 1 6 6 1 - [C1]₁₀

C2=A-B=-1184+477=-707

* *

1.1110 1110 0111 1011 [A]ок

0. 0000 0100 0111 0111 [-В]ок

1.1111 0010 1111 0010

0000 0110 0000 0110 в тетрада где был перенос +6(0110)

1.1111 1000 1111 1000

1.0000 0111 0000 0111 - [C2]_пк во всех тетрадах разрешенные комбинации,

- 0 7 0 7 - [C2]₁₀ следовательно коррекция не требуется

C3=-A+B=1184-477=707

* *

0.0001 0001 1000 0100 [-A]ок

1.1111 1011 1000 1000 [В]ок

10. 0000 1101 0000 1100 +1

0. 0000 1101 0000 1101

1010 1010 где не было переноса -6

0. 0000 0111 0000 0111 [C3]_пк

+ 0 7 0 7 [C3]₁₀

C4=-A-B=1184+477=1661

0. 0001 0001 1000 0100 [-A]ок

0. 0000 0100 0111 0111 [-В]ок

0.0001 0101 1111 1011

0110 0110 где больше 9 коррекция +6

0.0001 0110 0110 0001 [C4]_пк

+ 1 6 6 1 - [С4]₁₀

Задание 1.2. Выполнить операцию вычитания над числами А и В, представленными с плавающей точкой. А {а_п = +4 (порядок А), а_м = - 0.54 (мантисса А)}; В{b_п = +2 (порядок B), b_м = -0.80 (мантисса B)}. Использовать двоичный дополнительный код. При выполнении задания порядки и мантиссы операндов А и В необходимо представить в двоичной системе счисления и сформировать для них прямые коды. Разрядность модуля порядка должна быть равна 3, разрядность модуля мантиссы - 6 . Результат (порядок и мантисса) должен быть представлен в прямом коде в нормализованной форме.

Решение.

Результат вычисления С=А-В. Представим мантиссу и порядок чисел Аи В в двоичном прямом и дополнительном коде.

а_п = +4 [а]_пк=0.100

а_м = - 0.54

Мантисса А в двоичном виде:

2|54 [а_м]_пк=1.100010

1|08 [а_м]_дк=1.011110

0|16

0|32

0|64

1|28

0|56

b_п = +2 [b]_пк=0.010

b_м = -0.8

Мантисса В в двоичном виде:

2|8 [b_м]_пк=1.110011

1|6 [b_м]_дк=1.001101

1|2

0|4

0|8

1|6

1|2

Перед вычитанием производится выравнивание порядков. Число с меньшим порядком преобразуется в число с порядком, равным порядку другого числа(меньший порядок «приводится» к большему).

Чило B на четыре (4-(2)=2) порядка меньше числа A, следовательно мантиссу B необходимо сдвинуть на 2 разряда вправо. Тогда:

[С_п*]_пк=0.100

[b_м]_пк=1.00110011

[b_м]_дк=1.11001101

[-b_м]_пк=0. 00110011

[-b_м]_дк=0. 00110011

Далее производится вычитание как над числами с фиксированной запятой.

1.10001000

0. 00110011

1.10111011 [С_м]_дк

1.01000101 [С_м*]_пк

Для нормализации мантиссы сдвигаем её на один разряд влево, из предварительного порядка результата вычитаем один.

0.100 [С_п*]_пк

1.111 -1 дк

10.011

[С_п]_пк=0.011

Округляем модуль мантиссы до 6 знаков С_м=100011

Результат вычисления в нормализованной форме:

Мантисса-1. 100011, порядок-0.011

Задание 2.1

Построить цифровой автомат Мили для ГСА, приведенной на рисунке 2.1, используя D-триггер.

Рисунок 2.1.-Исходная ГСА для задания 2.1

Решение.

Формируем граф автомата Мили следующим образом:

• объединяются операционные вершины ГСА, для которых имеет место однозначная связь по входу и выходу, при условии, что результат выполнения микрооперации в предыдущей вершине не используется при выполнении микрооперации в последующей вершине;

• устраняются замкнутые пути из одной логической вершины ГСА в другую логическую вершину, минуя операторные вершины, посредством введения в этот путь пустой операторной вершины;

• во множество вершин графа автомата Мили включают начальную и конечную вершины ГСА;

• кроме того в качестве вершин графа автомата рассматриваются выходы операционных вершин ГСА (если выходы операционных вершин сходятся, то они рассматриваются как одна вершина графа цифрового автомата).

Результат приведен на рисунке 2.2

Рисунок 2.2

Объединенной кодированной таблицы переходов и выходов цифрового автомата составляется на основе всех существующих путей из вершин графа автомата. В таблице 2.1 приведена объединенной кодированной таблицы переходов и выходов для графа автомата Мили.

Таблица 2.1

N	Начало пути			Конец пути			логическое условие		выходной		Упр. памятью
пп	At	код At	At+1		код At+1			сигнал
1		000				1				0		0	1
3 4					010 011 100			-		0 0 1		1 1 0	0 1 0
5 6		010			100 100					1 1		0 0	0 0
7 8		011			011 100			-		0 1		1 0	1 0
9 10 11		100			100 101 101					1 1 1		0 0 0	0 1 1
12		101			110	1				1		1	0

При формировании этой таблицы использовалась кодировка состояний цифрового автомата двоичными эквивалентами их индексов. В качестве элемента памяти использован D-триггер. Таблица переходов D-тригера приведена в таблице 2.2.

Таблица 2.2- Таблица переходов D-триггера

D
0 0 1 1	0 1 0 1	0 0 1 1

.

На основании составленной таблицы логические выражения для выходных сигналов и сигналов управления памятью имею вид:

_ _ _ _ _ _ _ _ _ _ _ _ _

D₁=Q₁Q₂Q₃ х₂ х₄ + Q₁Q₂Q₃ х₅+ Q₁Q₂Q₃ х₅+ Q₁Q₂Q₃ х₄+ Q₁Q₂Q₃ х₁₀+

_ _ _ _ _ _

+Q₁Q₂Q₃ х₁₀ х₉ + Q₁Q₂Q₃ х₁₀ х₉+ Q₁Q₂Q₃ (4,5,6,8,9,10,11,12)

_ _ _ _ _ _ _

D₂= Q₁Q₂Q₃ х₂+ Q₁Q₂Q₃ х₂ х₄+ Q₁Q₂Q₃+Q₁Q₂Q₃ (2,3,7,12)

_ _ _ _ _ _ _ _ _ _ _

D₃= Q₁Q₂Q₃+ Q₁Q₂Q₃ х₂ х₄ + Q₁Q₂Q₃ х₄ + Q₁Q₂Q₃ х₁₀ х₉+Q₁Q₂Q₃ х₁₀ х₉

(1,3,7, 10,11)

_ _ _ _ _ _ _

Y₁=Q₁Q₂Q₃ + Q₁Q₂Q₃ х₂+ Q₁Q₂Q₃ (1,2,12)

_ _ _

Y₄=Q₁Q₂Q₃ (1)

_ _ _

Y₁₀=Q₁Q₂Q₃ (1)

_ _ _ _ _ _ _ _ _ _ _

Y₃= Q₁Q₂Q₃ х₂ + Q₁Q₂Q₃ х₂ х₄+ Q₁Q₂Q₃ х₄+ Q₁Q₂Q₃ х₉ х₁₀ (2,4,8,10)

_ _ _ _ _ _ _ _ _ _

Y₁₁= Q₁Q₂Q₃ х₂ + Q₁Q₂Q₃ х₂ х₄+ Q₁Q₂Q₃ х₄+ Q₁Q₂Q₃ х₉ х₁₀ (2,4,8,11)

_ _ _ _ _ _ _

Y₁₆= Q₁Q₂Q₃ х₅ + Q₁Q₂Q₃ х₅ + Q₁Q₂Q₃ х₁₀ (5,6,9)

_ _ _ _ _ _ _

Y₁₇= Q₁Q₂Q₃ х₅ + Q₁Q₂Q₃ х₅ + Q₁Q₂Q₃ х₁₀ (5,6,9)

_ _ _ _ _ _ _ _

Y₁₈= Q₁Q₂Q₃ х₅ + Q₁Q₂Q₃ х₁₀ + Q₁Q₂Q₃ х₁₀ х₉ (5,9,10)

_ _

Y₂₃= Q₁Q₂Q₃ х₅ (6)

_ _ _

Y₁₅= Q₁Q₂Q₃ х₁₀ х₉ (10)

_ _

Y₂₁= Q₁Q₂Q₃ х₁₀ х₉ (11)

_

Y₉= Q₁Q₂Q₃ (12)

_

Y_k=Q₁Q₂Q₃ (12)

После записи дизъюнктивной логической функций для выходных сигналов и сигналов управления разрядами памяти в скобках приведен перечень кодов используемых в этом выражении конъюнкций. В качестве этих кодов использованы номера строк в таблице, в которых отражается соответствующий путь.

На рисунке 2.3 приведена логическая схема, реализующая цифровой автомат, заданный графом на рисунке 2.2.

На вход схемы поступают проверяемые условия х₂, х₄, х₅, х₉, х₁₀. Обратные значения этих условий формируются с помощью трех схем НЕ.

На схеме каждый выход конъюнктивной части ПЛМ (горизонтальные линии) помечен кодом конъюнкции (номером строки в таблице), формируемой на этом выходе.

Выходом схемы является множество сигналы микроопераций у₁, у₄, у₁₀, у₃, у₁₁, у₁₆, у₁₇, у₁₈, у₂₃, у₁₅, у₂₁, у_9, у_к.

Рисунок 2.3.- Схема автомата Мили.

Задание 2.2

Написать микропрограмму, соответствующую ГСА приведенной на рисунке 2.4. В каждом адресе запоминающего устройства может храниться 16 бит информации. Обозначение у_к соответствует микрооперации, обозначающей последнюю микрокоманду в микропрограмме.

Управления объект, характеризуется следующими параметрами:

• множество проверяемых условий

• X ={x₁,x₁, .. x₃₁.};

• множество выполняемых микроопераций

• Y ={y₁,y₂, .. y₂₅, y_к} (y_к- микрооперация , означающая последнюю микрокоманду микропрограммы);

• ёмкость памяти для записи микропрограмм

• V_зу= 1кбайт = 2¹⁰ байт;

• длина ячейки памяти

• L = 16 бит;

• начальный адрес размещения составляемой микропрограммы в памяти

• А_н=500.

• 

Рисунок 2.4.-Исходная ГСА для задания 2.2.

Решение

Исходя из характеристик управляемого объекта, следует:

• длина поля для кодирования микроопераций равна к=5, так как количество выполняемых в объекте микроопераций равно 25

• (25 < 2⁵);

• длина поля для кодирования условий равна р=5, так как количество проверяемых условий в управляемом объекте равно 31 (31<2⁵);

• длина кода адреса равна р=10, так как количеству адресов в памяти, учитывая, что длина адресуемой ячейки равна 16 бит, т.е. двум байтам, равно (1000=<2¹⁰);.

Таким образом, формат микрокоманд для данного управляемого объекта имеет вид, приведенный на рисунке.

Рисунок 2.5

Формат операционной микрокоманды (МКО) имеет длину 16 бит и включает:

• поле типа микрокоманды (Т), имеющее длину в один бит и занимающее 0-ой разряд микрокоманды; в этом поле для данного типа микрокоманды записано значение «1»;

• поле первой микрооперации (Y₁), которое занимает разряды с 1-го по 5;

• поле второй микрооперации (Y₂), которое занимает разряды с 6-го по 10;

• поле микрооперации у_к, которое используется только в последней микрокоманде для указания завершения выполнения микропрограммы.

Формат микрокоманды перехода (МКП) имеет длину 16 бит и включает:

• поле типа микрокоманды (Т), имеющее длину в один бит и занимающее 0-ой разряд микрокоманды; в этом поле для данного типа микрокоманды записано значение «0»;

• поле проверяемого условия (Х), которое занимает разряды с 1-го по 5;

• поле адреса (А), которое занимает разряды с 6-го по 15;

• поле модификатора дисциплины перехода не используется. адрес следующей микрокоманды А_с формируется как:

 А_т + 1, если х_i =0;

А_с = 

А, если х_i =1,

А - адрес перехода, располагаемый в одноименном поле выполняемой микрокоманды перехода.

Микропрограмма, реализующая приведенную ГСА, имеет вид, приведенный в таблице 2.3.

Таблица 2.3.

N пп	N вер.	Адрес расположения микрокоманды в ЗУ	Код микрокоманды
	1	0111110100 (Ан=500)	1. 00001 . 11111. 0
	2	0111110101	1. 00010 . 01011. 0
	3	0111110110	0. 00011. 111110101
	4	0111110111	1. 01011. 10100. 0
	-	0111111000	1. 01101. 00000. 0
	5	0111111001	1. 11011. 01010. 0
	6	0111111010	1. 01011 . 10100. 0
	-	0111111011	1. 01101. 00000. 0
	7	0111111100	0. 0011. 0111111110
	-	0111111101	0. 0000. 0111111010
	8	0111111110	0. 0111. 0111111100
	9	0111111111	0. 0010.1000000010
	10	1000000000	1. 01001 . 01100. 0
	-	1000000001	1. 10101. 00000. 0
	12	1000000010	1. 01001 . 01100. 0
	-	1000000011	1. 01111. 00000. 0
	11	1000000100	1. 00100 . 01011. 1

В приведенной таблице:

• в первой, самой левой, колонке фиксируется номер строки;

• в первой графе (помечена «1») приводится номер вершины, реализуемой микрокомандой этой строки;

• во второй графе указан адрес расположения данной микрокоманды в запоминающем устройстве;

• в третьей графе располагается код микрокоманд;

• в четвертой графе указаны номера вершин (вершина-ссылка), адреса которых указываются в соответствующей команде перехода.