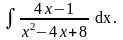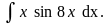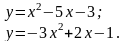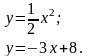Общие методические указания

Внешнюю обложку тетради следует оформить в соответствии с общими требованиями оформления учебного заведения.

Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления необходимо делать полностью. Для замечаний преподавателя нужно на каждой странице оставлять поля.

В конторольной работе 15 вариантов. Номер варианта студент выбирает в соответствии со следующей таблицей

№ вар.	1	2	3	4	5	6	7	8	9	10
№ в журнале	1	2	3	4	5	6	7	8	9	10
	11	12	13	14	15	16	17	18	19	20
	21	22	23	24	25	26	27	28	29	30

Перед выполнением каждой контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и может воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях.

Задания для выполнения контрольной работы (ргр)

Задание 1.

Найти неопределенные интегралы способом подстановки (методом замены переменной).

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

Решение типовых примеров.

1. Найти неопределенный интеграл

Решение. Применим подстановку 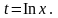Тогда и

2. Найти интеграл

Решение. Применим подстановку . Тогда откуда

Задание 2.

Найти неопределенные интегралы, используя выделение полного квадрата.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.

Решение типового примера. Найти интеграл

Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:

Тогда после подстановки получаем

При этом при вычислении интеграла мы воспользовались заменой переменной 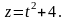Тогда откуда

Задание 3.

Найти неопределенные интегралы, применяя метод интегрирования по частям.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.

Решение типовых примеров.

1. Найти интеграл

Решение. Применим формулу интегрирования по частям

Положим Тогда Следовательно,

2. Найти интеграл .

Решение. Положим u = arctg 3x, dv = dx. Тогда . Отсюда

Применяя в последнем интеграле подстановку

получаем следовательно,

Отсюда

Задание 4.

Найти неопределенные интегралы, пользуясь разложением рациональных дробей на простейшие.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.

Решение типовых примеров.

1. Найти интеграл

Решение. Разложим знаменатель на множители

Тогда

Освобождаемся от знаменателя:

.

Теперь приравниваем коэффициенты при одинаковых степенях х:

Из второго уравнения получаем

Отсюда

Следовательно,

Воспользуемся равенством

После замены переменной и

Ответ:

2. Найти интеграл

Решение. Из равенства

получаем

Приравниваем коэффициенты при одинаковых степенях х:

Отсюда Таким образом,

Задание 5.

Вычислить площадь, ограниченную заданными параболами.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.

Решение типового примера. Вычислить площадь, ограниченную параболами (рис.4)

Решение. Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:

Отсюда

Вычисление площади осуществляем по формуле

где − кривые, ограничивающие фигуру ( ).

В нашем случае

Задание 6.

Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью Ох.

1.
2.
3.
7.
8.
9.
10.

Решение типового примера. Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной параболой , прямой и осью Ох (рис.5).

Рис.5

Решение. Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение

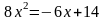
или Легко убедиться, что Первому квадранту соответствует корень

Найдем теперь абсциссу точки пересечения прямой с осью Ох, решив уравнение откуда

Таким образом, можно считать, что тело вращения ограничено при поверхностью, образованной вращением параболы вокруг оси Ох, а при − вращением прямой .

Искомый объем ищем по формуле

Для вычисления второго интеграла используем подстановку

. Тогда и

Отсюда

Задание 7.

Вычислить частные производные первого и второго порядков от заданных функций.

Решение типового примера. Пусть

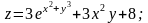
При вычислении частной производной переменную y рассматриваем как постоянную величину. Пользуясь правилом дифференцирования функции одного аргумента и, в частности, правилом дифференцирования сложной функции, получаем

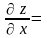
Аналогично поступаем при вычислении . Считая х постоянной величиной, получаем

=

Используя те же правила, вычисляем частные производные второго порядка:

Задание 8.

Задана функция z = f(x, y). Найти градиент и производную этой функции в заданной точке М (х_о, у_о) в направлении вектора , составляющего угол с положительным направлением оси Ох.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

Решение типового примера. Пусть

Найдем градиент и производную этой функции в точке в направлении, составляющем угол с положительным направлением оси Ох. Для этого вычислим частные производные функции:

Вычислим теперь значения этих производных в точке :

Таким образом,

Производная в направлении вектора , составляющего угол с положительным направлением оси Ох вычисляется по формуле

,

т.е. в нашем случае

.

Задание 9.

Найти экстремум заданной функции.

1.
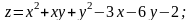
2.
3.
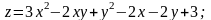
4.
5.
6.
7.
8.
9.
10.

Решение типового примера. Пусть

Находим частные производные функции:

Воспользовавшись необходимыми условиями экстремума, находим стационарные точки. Для этого решаем систему уравнений

откуда х = 1; у = 2. Таким образом, стационарной является точка М (1, 2).

Находим значения частных производных второго порядка в точке М:

Составляем выражение

Так как , делаем вывод о наличии минимума в точке

М(1, 2). При этом минимальное значение функции равно