Прискорення будь-якої точки плоскої фігури дорівнює геометричній сумі прискорення полюса, дотичного і нормального прискорень цієї точки при обертанні її навколо полюса.

Але геометрична сума дотичного і нормального прискорень є повним прискоренням точки при її обертанні навколо полюса :

. (3.15)

Модуль прискорення знаходиться з формули . З урахуванням виразів (3.11) і (3.13), маємо:

. (3.16)

Кут між векторами і позначимо через . Тоді напрям прискорення знайдемо з виразу:

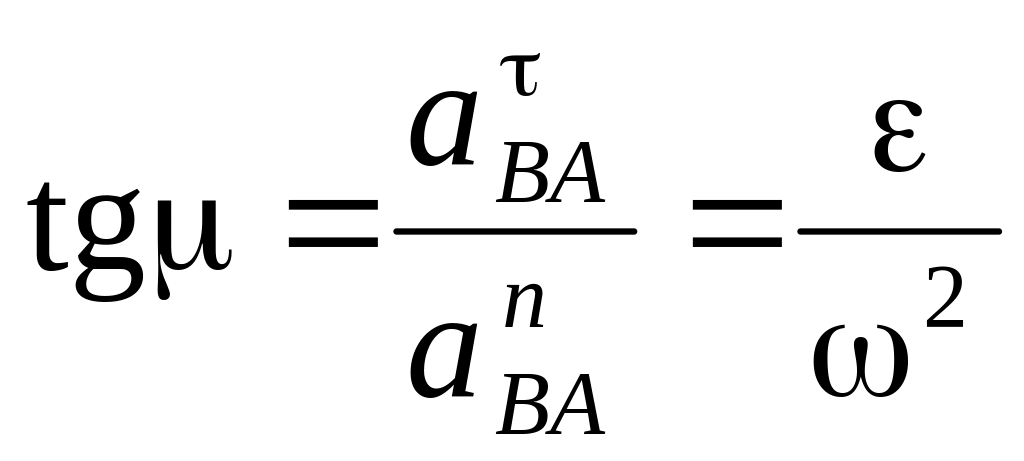_. (3.17)

З цього виразу видно, що для всіх точок плоскої фігури в даний момент часу кут однаковий, тому що відношення не залежить від положення точок плоскої фігури.

Співвідношення (3.14) можна записати в іншому виді:

. (3.18)

Щоб побудувати вектор прискорення точки , доцільно спочатку отримати вектор як суму і . Потім на векторі і векторі , перенесеному в точку , побудувати паралелограм, діагональ якого відповідає вектору прискорення точки .

Миттєвий центр швидкостей

Покажемо, що при плоскому русі існує така точка фігури, швидкість якої у даний момент часу дорівнює нулю, і тіло в цей час виконує миттєвий обертальний рух навколо осі, що проходе через цю точку.

Нехай тіло при плоскому русі в даний момент часу має кутову швидкість , а точка – швидкість (рис. 3.8).

П роведемо через точку перпендикуляр до вектора швидкості . Візьмемо на цьому перпендикулярі точку . На основі (3.4) для точки запишемо , де швидкість . В точці швидкості і напрямлені протилежно, тому .

З урахуванням отримуємо . Змінюючи положення точки на перпендикулярі, тобто змінюючи відстань , можна знайти таке положення точки , при якому швидкість . Звідси

. (3.19)

Т очка плоскої фігури, швидкість якої в даний момент часу дорівнює нулю, називається миттєвим центром швидкостей.

Вивчимо розподіл швидкостей точок плоскої фігури, якщо відомий миттєвий центр швидкостей . Поставимо у цю точку полюс (рис. 3.9), тоді швидкості довільних точок і рівні: ; . Так як , то , . Швидкості , . Це означає, що

, . (3.20)

Так як , , то

, , (3.21)

, – називаються миттєвими радіусами обертання.

Візьмемо відношення . Маємо:

і . (3.22)

Можна зробити висновки:

1. Швидкості точок плоскої фігури в даний момент часу розподіляються так само, як при обертанні фігури навколо осі, що проходить через миттєвий центр швидкості перпендикулярно площині фігури.

2. Модуль швидкості будь-якої точки плоскої фігури в кожний момент часу дорівнює добутку кутової швидкості тіла на миттєвий радіус обертання точки. Вектор швидкості перпендикулярний миттєвому радіусу обертання.

3. Відношення швидкостей двох точок плоскої фігури прямо пропорційне відношенню відстаней цих точок до центра швидкостей.

4. Кутова швидкість обертання навколо миттєвого центра швидкостей визначається за допомогою формули .

5. Миттєвий центр швидкостей знаходиться на перетині перпендикулярів до векторів швидкостей у даних точках.

Слід миттєвого центра швидкостей у нерухомій площині називається миттєвим центром обертання плоскої фігури. Миттєвий центр швидкостей – точка рухомої плоскої фігури, а миттєвий центр обертання – точка нерухомої площини, по якій рухається плоска фігура.

Геометричне місце миттєвих центрів швидкостей називається рухомою центроїдою, а геометричне місце миттєвих центрів обертання називається нерухомою центроїдою. При всякому непоступальному русі плоскої фігури рухома центроїда котиться по нерухомій центроїді.