Лекція № 4.
Тема 3. Плоский рух твердого тіла
Означення плоского руху
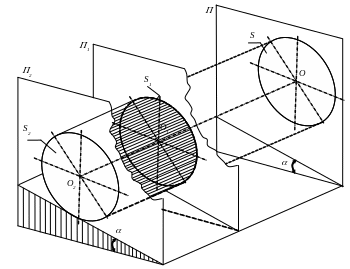
Якщо всі точки тіла рухаються в площинах, паралельних деякій нерухомій площині, то такий рух тіла називається плоскопаралельним (плоским) рухом тіла.
|
Рис 3.1 |
На
рис. 3.1 показано рух круглого циліндричного
катка. Проведемо нерухому площину
,
яка перпендикулярна осі обертання
катка. Проведемо площини
,
і т.д., які паралельні площині
і перетинають тіло катка. Отримали
кругові перерізи
,
і т.д. Якщо при русі катка всі перерізи
,
і т.д. будуть залишатись в площинах
,
і т.д., то в цьому випадку тіло виконує
плоский рух. В подальшому площини
,
будемо суміщати з нерухомою площиною
,
а замість всього тіла будемо зображати
тільки переріз
в нерухомій площині і вивчати рух цієї
плоскої фігури.
Рівняння плоского руху твердого тіла
Як уже відмічалось раніше, плоский рух твердого тіла тотожний руху його плоского перерізу. Тому в подальшому будемо розглядати рух тільки перерізу тіла, сумістивши його для зручності з площиною рисунка.
Н
ехай
тіло виконує плоский рух. Розглянемо
рух плоского перерізу
цього тіла (рис. 3.2). В площині руху фігури
виберемо систему координат
.
Візьмемо на площині
точки
і
та проведемо вектор
.
Тоді
, (3.1)
де
і
– радіус-вектори відповідно точок
і
тіла.
З
плином часу радіус-вектори
,
змінюються, тобто є функціями часу. При
русі тіла відстань між точками
і
не змінюється
(тіло
тверде), тобто модуль вектора
,
але змінюється напрям
вектора
завдяки тому, що фігура
може обертатись в площині
.
Це означає, що вектор
є функцією часу
. (3.2)
Вирази (3.1) і (3.2) є векторними рівняннями плоского руху твердого тіла.
Плоский рух як поступальний рух полюса і обертальний навколо полюса
Н
ехай
тіло виконує плоский рух. Рух цього тіла
будемо розглядати як
рух
відрізка
(рис. 3.3). Нехай у початковий момент часу
тіло займало положення
,
а через проміжок часу
– положення
,
в якому відрізок
зайняв положення
.
Яким чином відрізок
перетворився у
?
Візьмемо
за полюс точку
.
Нехай тіло рухалось поступально, і точка
потрапила в точку
.
Тоді точка
відрізка
повинна потрапити в точку
.
Щоб точка
потрапила в положення
,
необхідно,
щоб тіло виконало обертальний рух на
кут
навколо точки
(полюса).
Таким чином, плоский рух тіла можна розглядати як суму двох простих рухів: 1) поступального руху тіла разом з полюсом, 2) обертального руху тіла навколо полюса.
Яку ж точку тіла обрати за полюс і що зміниться, якщо змінити полюс?
Візьмемо
за полюс точку
.
Нехай
тіло
з положення
рухається поступально і точка
потрапила в точку
.
Тоді
точка
потрапляє в положення
.
Щоб
точка
потрапила в положення
,
необхідно тілу надати
обертальний
рух на кут
навколо точки
.
Проаналізуємо
ці два
випадки.
По-перше, при обертальному русі
і, по-друге, напрям обертання однаковий.
Висновок: 1. Вибір полюса не впливає на обертальний рух тіла, тобто значення кутової швидкості і кутового прискорення тіла не будуть залежати від вибору полюса. 2. Вибір полюса впливає на поступальний рух тіла.
З
апишемо
рівняння плоского руху тіла інакше.
Виберемо систему координат у площині
руху плоскої фігури (рис. 3.4)
та відрізок
на твердому тілі. Візьмемо за полюс
точку
.
Запишемо такі рівняння:
,
,
. (3.3)
Перші два рівняння виразу (3.3) характеризують рух точки , тобто характеризують поступальний рух тіла. Третє рівняння виразу (3.3) характеризує обертальний рух тіла навколо полюса . Отже, рівняння (3.3) є рівняннями плоского руху твердого тіла в координатній формі.
Розглянемо окремі випадки плоского руху тіла.
1. Нехай полюс не рухається. Тоді тіло буде виконувати обертальний рух навколо точки . Це означає, що обертальний рух тіла є одним із видів плоского руху.
2.
Нехай при плоскому русі тіла кут
,
тобто тіло не обертається навколо полюса
.
Це означає, що тіло виконує поступальний
рух в одній площині.