Файловый архив студентов. Файловый архив студентов.
1308 вузов, 5223 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Рязанский государственный радиотехнический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
тр.doc
Скачиваний:
3
Добавлен:
12.07.2019
Размер:
2.01 Mб
Скачать
☆
►Содержание►

Тема 3. Элементы аналитической геометрии Теоретические вопросы

  1. Общее уравнение плоскости в пространстве. Различные уравнения плоскости в пространстве.

2. Взаимное расположение двух плоскостей в пространстве: угол между двумя плоскостями, условия параллельности и перпендикулярности двух плоскостей. Расстояние от точки до плоскости.

3. Различные уравнения прямой линии в пространстве (с опорной точкой и направляющим вектором, через две опорные точки, каноническое, параметрические, по двум пересекающимся плоскостям).

4. Взаимное расположение двух прямых в пространстве (угол между двумя прямыми, условия параллельности, перпендикулярности, пересечения, сливания и скрещивания двух прямых в пространстве).

5. Взаимное расположение прямой и плоскости в пространстве (угол между прямой и плоскостью, условия параллельности и перпендикулярности прямой и плоскости). Нахождение точки пересечения прямой и плоскости.

6. Различные уравнения прямой на плоскости: с опорной точкой и направляющим вектором, через две точки, с угловым коэффициентом, с опорной точкой и вектором нормали, общее уравнение и его частные случаи, в отрезках на осях. Расстояние от точки до прямой.

7. Взаимное расположение двух прямых на плоскости: угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых.

Расчетные задания

Задание 17 (Аналитическая геометрия в пространстве)

Даны координаты точек M, N, P, Q (см. ниже).

1. Найти координаты векторов , разложить их по базисным ортам прямоугольной декартовой системы координат, найти длины (модули) векторов.

2. Вычислить косинус угла между рёбрами MN и MP.

3. Найти площадь грани MNP.

4. Вычислить проекцию вектора на вектор .

5. Найти направляющие косинусы вектора .

6. Вычислить объём пирамиды MNPQ (двумя способами).

7. Найти длину высоты пирамиды, опущенной из точки .

8. Написать общие уравнения плоскостей MNP, MPQ, привести к нормальному виду и к виду уравнения в отрезках на осях (сделать проверку), найти угол между этими плоскостями.

9. Написать общее уравнение плоскости , проходящей через точку Q, параллельно плоскости MNP.

10. Написать общее уравнение плоскости , проходящей через точки , перпендикулярно плоскости MNP.

11. Написать канонические и параметрические уравнения прямой , образованной в результате пересечения плоскостей , ( ).

12. Написать канонические и параметрические уравнения прямых , .

13. Написать канонические и параметрические уравнения прямой , проходящей через точку , перпендикулярно плоскости MNP.

14. Написать канонические и параметрические уравнения прямой , проходящей через точку , параллельно прямой .

15. Найти точку пересечения прямой с плоскостью MNP.

16. Найти угол между прямой и плоскостью MNP.

Исходные координаты точек M, N, P, Q (в cоответствии с вариантами)

  1. М(–3, –2, –4), N(–4, 2, –7), P(5, 0, 3), Q(–1, 3, 0);

  2. М(2, –2, 1), N(–3, 0, –5), P(0, –2, –1), Q(–3, 4, 7);

  3. М(1, 3, 2), N(3, 2, 7), Р(4, 0, 0), Q(–2, 1, 2);

  4. M(3, 6, –2), N(0, 2, –3), Р(1, –2, 0), Q(–7, 6, 6);

  5. М(1, –4, 1), N(4, 4, 0), P(–1, 2, –4), Q(–9, 7, 8);

  6. М(1, –2, 1), N(3, 1, –2), Р(2, 2, 5), Q(–2, 1, 0);

  7. М(0, 6, –5), N(8, 2, 5), Р(2, 6, –3), Q(5, 0, –6);

  8. М(–2, 4, –6), N(0, –6, 1), Р(4, 2, 1), Q(7, –1, –8);

  9. М(–4, –2, –5), N(1, 8, –5), P(0, 4, –4), Q(9, –2, –10);

  10. М(3, 4, –1), N(2, –4, 2), P(5, 6, 0), Q(11, –3, –12);

  11. М(2, –3, 1), N(6, 1, –1), Р(4, 8, –9), Q(2, –1, 2);

  12. М(5, –1, –4), N(9, 3, –6), Р(7, 10, –14), Q(5, 1, –3);

  13. М(1, –4, 0), N(5, 0, –2), Р(3, 7, –10), Q(1, –2, 1);

  14. М(–3, –6, 2), N(1, –2, 0), Р(–1, 5, –8), Q(–3, –4, 3);

  15. М(–1, 1, –5), N(3, 5, –7), Р(1, 12, –15), Q(–1, 3, –2);

  16. М(1, –3, –4), N(–1, 0, 2), Р(2, –4, –6), Q(1, 1, 1);

  17. М(0, 4, 3), N(4, 8, 1), Р(2, 15, –7), Q(0, 6, 4);

  18. М(–2, 0, –2), N(2, 4, –4), Р(0, 11, –12), Q(–2, 2, –1);

  19. М(3, 3, –3), N(7, 7, –5), Р(5, 14, –13), Q(3, 5, –2);

  20. М(1, 1, –1), N(0, 1, 2), Р(5, 4, –3), Q(0, 2, –6);

  21. М(1, 1, 1), N(2, 2, 2), Р(5, –4, –3), Q(1, –2, –6);

  22. М(1, 1, 2), N(3, 5, –2), Р(2, 3, –5), Q(0, –3, 2);

  23. М(0, –1, 2), N(2, 0, –4), Р(1, 2, 5), Q(4, –1, 3);

  24. М(0, 1, –2), N(–2, 0, 2), Р(1, 2, 3), Q(4, –2, 1);

  25. М(0, 6, –5), N(8, 2, 5), Р(2, 6, –3), Q(5, 0, –6);

  26. М(0, 2, 3), N(3, –2, –1), Р(2, 6, –3), Q(4, 0, –6);

  27. М(1, 2, 3), N(2, 4, 6), Р(2, 6, 0), Q(3, 2, –1);

  28. М(–1, –2, –3), N(–2, –4, –6), Р(–2, 1, 0), Q(–3, 2, 1);

  29. М(1, 4, 0), N(–4, 2, 2), P(1, 2, –3), Q(0, 7, 2);

  30. М(0, 4, 3), N(4, 8, 1), Р(2, 15, –7), Q(0, 6, 4).

Задание 18 (Аналитическая геометрия в пространстве). Решить задачу.

    1. Выяснить, лежат ли точки М(–1, 2, –2), N(1, 0, 5), Р(–3, 4, –9) на одной прямой . Найти уравнение этой прямой и представить его во всех формах записи. Написать уравнение плоскости , проходящей через точку (0, 2, 5) и содержащей прямую .

    2. Написать уравнение плоскости , проходящей через точки , и прямую .

    3. Даны плоскость : и прямая , являющаяся пересечением двух плоскостей , . 1. Написать уравнение плоскости , содержащей в себе прямую и перпендикулярной к плоскости . 2. Найти расстояние от точки до плоскости . 3. Найти угол между плоскостями , .

    4. Выяснить, как расположены относительно друг друга прямые, заданные уравнениями ,

    5. Написать уравнение плоскости , проходящей через точки , параллельно прямой .

    6. Даны две плоскости , . Найти: 1) угол между плоскостями; 2) уравнение прямой (записать уравнение прямой во всех видах), по которой пересекаются плоскости.

    7. Заданы плоскость : и прямая .

1. Вычислить угол между плоскостью и прямой . 2. Найти координаты точки пересечения прямой с плоскостью. 3. Написать уравнение плоскости , содержащей прямую , перпендикулярную к плоскости .

    1. Написать уравнение плоскости , проходящей через точки , , перпендикулярно к плоскости : . Найти расстояние от точки до плоскости и уравнение линии пересечения плоскостей , .

    2. Написать уравнение прямой как линию пересечения плоскостей : , . Найти расстояние от точки 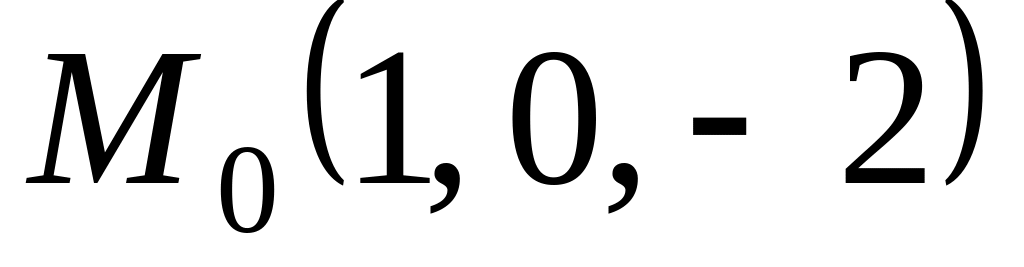до этой прямой . Выяснить вопрос о взаимном расположении прямой и прямой .

    3. Написать уравнение прямой как линию пересечения плоскостей : , . Найти расстояние от начала координат до этой прямой . Написать уравнение плоскости, проходящей через начало координат и содержащей прямую .

    4. Написать уравнение прямой , проходящей через точку , параллельно прямой : Найти расстояние от точки до этой прямой .

    5. Установить, что точки М(1, 2, 3), N(10, 8, 4), Р(1, 2, 3) лежат на одной прямой . Найти уравнение этой прямой и представить его во всех формах записи. Написать уравнение плоскости , проходящей через точку (0, 2, 5) и содержащей прямую .

    6. Составить общее уравнение плоскости , проходящей через точку параллельно векторам (–5, 6, 4), (2, –1, 0). Сделать проверку правильности составления уравнения плоскости . Выяснить, принадлежит ли плоскости точка .

    7. Составить уравнение плоскости, проходящей через прямую , , и точку М(–2, 3, 0). Выяснить, принадлежит этой плоскости точка .

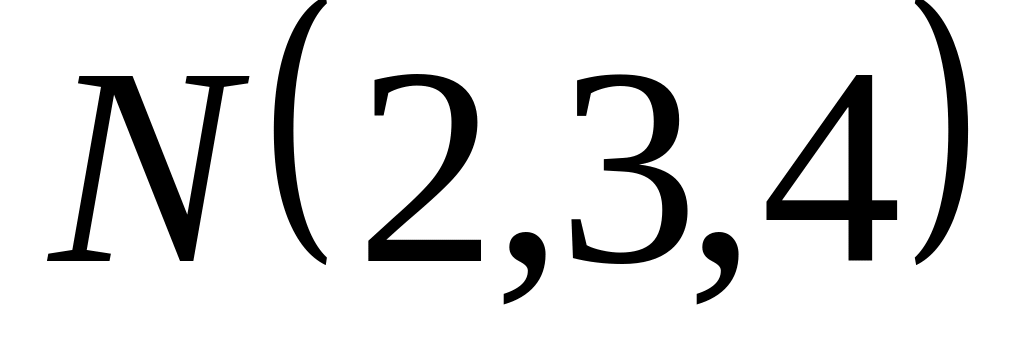    8. Написать уравнение плоскости, проходящей через начало координат и через линию пересечения плоскостей . Найти угол между этими плоскостями.

    9. Составить: 1) уравнение плоскости , проходящей через точку и содержащей прямую 2) уравнение прямой, проходящей через точку и перпендикулярно к прямой .

    10. Составить уравнение прямой , проходящей через :

1) параллельно прямой : 2) перпендикулярно к прямой ;

3) написать уравнение плоскости , содержащей точку и .

    1. Доказать, что прямые параллельны, и найти расстояние между ними.

    2. Проверить, лежат ли прямые : и : в одной плоскости. Если лежат, то найти общее уравнение этой плоскости.

    3. Составить общее уравнение плоскости , проходящей через прямую : , параллельно прямой . Выяснить, принадлежит ли точка этой прямой.

    4. Найти координаты точки пересечения прямой : и плоскости .

    5. Найти угол между прямой : и плоскостью : . Через точку проведен перпендикуляр к плоскости . Найти площадь треугольника, образованного точкой , точкой пересечения прямой с плоскостью и точкой пересечения прямой с плоскостью . Сделать схематический рисунок к задаче.

    6. Заданы плоскость : и точка . Написать уравнение плоскости , проходящей через точку параллельно . Найти расстояние между этими двумя плоскостями (сделать рисунок).

    7. Проверить, лежат ли прямые и в одной плоскости. Если лежат, то найти общее уравнение этой плоскости.

    8. Найти угол между прямыми и

    9. Написать уравнение плоскости , проходящей через точки , 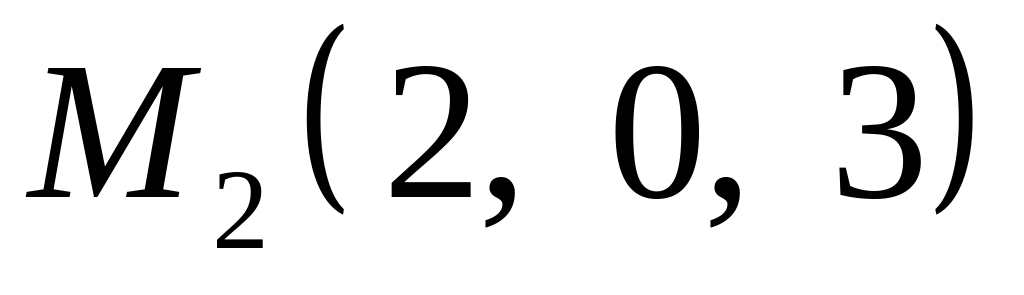и прямую

    10. Даны две плоскости , . Найти: 1) угол между плоскостями; 2) уравнение прямой (записать уравнение прямой во всех видах), по которой пересекаются плоскости.

    11. Составить: 1) уравнение плоскости , проходящей через точку и содержащей прямую 2) уравнение прямой, проходящей через точку перпендикулярно к прямой .

    12. Выяснить, как расположены в пространстве прямые, заданные уравнениями .

    13. Найти угол между прямыми, заданными уравнениями

Задание 19 (Аналитическая геометрия на плоскости)

Даны вершины треугольника MNP (координаты точек см. ниже). Сделать чертёж в прямоугольной декартовой системе координат (чертеж выполнить в соответствии с масштабом). Найти:

1) длины сторон треугольника MNP;

2) общие уравнения сторон (MN) , (NP), (MP) и их угловые коэффициенты;

3) угол N (через косинус и тангенс);

4) общее уравнение высоты (PQ) и её длину;

5) общее уравнение медианы (MR), координаты точки S пересечения ее с высотой (PQ);

6) уравнение прямой, проходящей через точку S параллельно стороне MN.

Написать линейную систему ограничений, описывающую внутренность треугольника (включая границы треугольника).

№

Координаты М, N, P

№

Координаты М, N, P

1

М(–3, 9), N(2, 0), P(7, 4);

2

М(0, 2), N(10, –1), Р(6, 7);

3

М(–4, 6), N(3, –3), P(7, 9);

4

М(1, 8), N(5, 3), Р(­3, 0);

5

М(–2, –1), N(0, 10), Р(4, 12);

6

М(–4, ­4), N(5, 5), Р(1, –4);

7

М(2, 5), N(10, –4), P(0, –3);

8

М(–1, –3), N(8, 3), Р(4, 7);

9

М(–2, 1), N(10, 0), P(5, 7);

10

М(–6, 8), N(1, 1), Р(4, 5);

11

М(3, 6), N(10, –3), Р(13, 11);

12

М(–10, 5), N(1, –1), Р(0, 10);

13

М(–4, 5), N(0, 0), Р(9, 7);

14

М(–3, –3), N(9, 1), Р(7, 10);

15

М(4, 1), N(–5, –5), Р(0, 8);

16

М(7, 4), N(5, –5), Р(–3, 1);

17

М(0, 3), N(8, 10), Р(4, –3);

18

М(0, 4), N(4; 0), Р(7, 7);

19

М(0, –2), N(–4, 0), Р(7, 7);

20

М(2, 2), N(6, –2), Р(8, 6);

21

М(–3, 0), N(3, 3), Р(2, –5);

22

М(3, –5), N(–4, –4), Р(2, 5);

23

М(5, 2), N(–4, 4), Р(–2, –5);

24

М(–9, 6), N(3, –3), P(7, 4);

25

М(4, 2), N(4, –4), P(6, 8);

26

М(0, 0), N(–4, 6), P(6, 8);

27

М(0, –4), N(10, 9), Р(1, 15);

28

М(0, 3), N(10, –6), Р(5, 8);

29

М(–5, –3), N(4, –5), Р(3, 8);

30

М(–5, 1), N(7, –2), P(1, 7).

Библиографический список

  1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1983. – 243 c.

  2. Гельфанд И. М. Лекции по линейной алгебре. Изд. 6-е. – М.: Наука, 1984. 336 c.

  3. Икрамов Х.Д. Задачник по линейной алгебре. – М.: Наука, 1975. – 320 c.

  4. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1999. – 304 c.

  5. Мальцев А.И. Основы линейной алгебры. – М.: Наука, 1970. – 324 c.

  6. Проскуряков И. В. Сборник задач по линейной алгебре. 5-е изд. – М.: Наука, 1974. – 384 c.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности