4. ТИПОВОЙ РАСЧЕТ №4
Контрольная работа соответствует разделу программы «Переходные процессы в линейных электрических цепях. Операторный метод расчёта переходных процес- сов».
Задание для контрольной работы генерируется ЭВМ каждому студенту индивиду- ально.
Распечатка одного из вариантов задания представлена на рис. 3.10. В контрольной работе необходимо:
1.Записать шифр задания.
2.Получить и записать исходные данные контрольной работы по распечатке, на- чертить схему цепи.
3.Рассчитать операторным методом переходные процессы по току в индуктивно-
сти i3 (t) и по напряжению на ёмкости uC (t) .
56
PDF created with pdfFactory Pro trial version www.pdffactory.com
4. По результатам расчётов построить график переходных процессов.
Рассмотрим выполнение варианта контрольной работы, представленного на рис. 3.10, с необходимыми комментариями:
1.Шифр задания 13040616 записан на карточке слева.
2.Для получения исходных данных контрольной работы необходимо изобразить схему электрической цепи. Для этого вместо R1, R2, R3 на графической части лист- ка с заданием начертить активные сопротивления, вместо С – ёмкость, вместо L – индуктивность, вместо Е – источник ЭДС. Ключ К1 должен быть разомкнут. Ком- мутация происходит путём переключения клю- ча К2 из положения 1 в положение 2. Величины
сопротивлений заданы в строке ПАРАМЕТРЫ листка, величины индуктивностей и ёмкостей – в строке ОПЕРАТОРНЫЙ МЕТОД: r1 = 100 Oм; r2 = 24 Oм; r3 = 21 Oм; L = 10 мГн; С = 0,54 мкФ.
Для всех вариантов задания Е = 100 B.
Схема электрической цепи приведена на рис. 4.1.
3.Расчёт переходных процессов операторным
методом основан на использовании преобразо- вания Лапласа. Это позволяет перейти от непосредственного решения дифференци-
альных уравнений, описывающих цепь во временной области, к решению алгеб- раических уравнений в области изображений.
Расчёт переходных процессов операторным мето- дом производится в следующем порядке:
–рассчитывается цепь до коммутации с целью оп- ределения независимых начальных условий;
–составляется операторная схема замещения цепи;
–производится расчёт операторной схемы замеще- ния, в результате чего определяются изображения по Лапласу искомых функций;
на основе обратного преобразования Лапласа от найденных изображений переходят к оригиналам. Расчёт переходных процессов в цепи, представ- ленной на рис. 4.1, произведём в предложенном порядке.
До коммутации в цепи был включён источник постоянного напряжения. На посто- янном токе индуктивность обладает нулевым сопротивлением, а ёмкость – беско- нечно большим. В эквивалентной схеме цепи для расчёта независимых начальных условий, изображённой на рис. 4.2, реактивные элементы показаны как короткое замыкание и обрыв.
Ток в цепи с индуктивностью определится выражением
i3 |
(0−) = |
|
E |
= |
|
100 |
|
|
= 0,826 А. |
|
r1 |
+ r3 |
100 + |
21 |
|||||||
|
|
|
|
|||||||
57
PDF created with pdfFactory Pro trial version www.pdffactory.com
Напряжение на ёмкости будет равно
uC (0-) = i3 (0-) × r3 = 0,826 × 21 =17,35 В.
Согласно законам коммутации ток в индуктивности и напряжение на ёмкости в момент коммутации не могут измениться скачком. Следовательно,
i3 (0-) = i3 (0+) = 0,826 А; uC (0-) = uC (0+) =17,35 В.
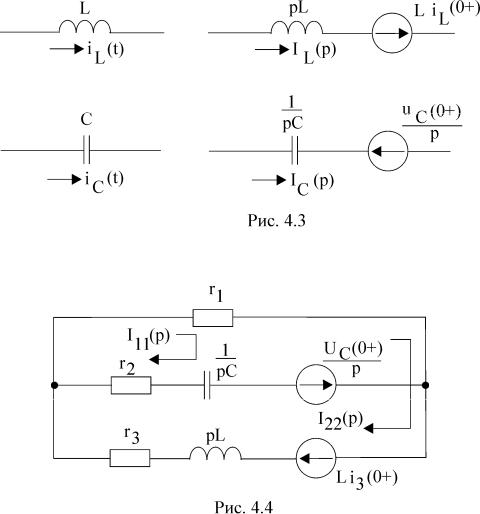
При составлении операторной схемы замещения все элементы цепи замещаются их операторными эквивалентами. Так, индуктивность замещается операторным ин- дуктивным сопротивлением pL, ёмкость – операторным ёмкостным сопротивлени- ем 1/pС, активное сопротивление не изменяется. При этом ненулевые начальные
условия учитываются в цепях с индуктивностью и с ёмкостью дополнительными источниками ЭДС (рис. 4.3).
Операторная схема замещения послекоммутационной цепи для рассматриваемого примера, построенная в соответствии с изложенным выше, приведена на рис. 4.4.
Для расчёта операторной схемы замещения может быть применён любой извест- ный метод: метод узловых потенциалов, метод наложения, метод контурных токов и т.д. Однако целесообразно использовать метод контурных токов, который при надлежащем выборе независимых контуров обеспечивает наиболее быстрое полу- чение конечного результата.
Выберем независимые контуры таким образом, чтобы общая ветвь содержала толь-
58
PDF created with pdfFactory Pro trial version www.pdffactory.com
ко сопротивление r1 . Тогда контурные токи I11(p) и I22 (p) будут равны изображе-
ниям токов в индуктивности и в ёмкости.
Уравнения, описывающие цепь на рис. 4.4 по методу контурных токов, запишутся в
виде
æ |
|
|
1 |
ö |
|
|
|
|
u |
C |
(0+) |
, |
çr |
+ r + |
|
÷I |
(p) + r I |
22 |
(p) = |
|
|
||||
|
|
|
|
|||||||||
ç |
1 |
2 |
|
÷ |
11 |
1 |
|
|
|
p |
|
|
è |
|
|
pC ø |
|
|
|
|
|
|
|
||
r1I11(p) + (r1 + r3 + pL)I22 (p) = Li3 (0+) .
Решая полученную систему с помощью определителей, получим
|
|
p[LC(uC (0+) + i3 (0+)r1)]+ C(r1 + r3 )uC (0+) |
|
|
|
||||||||||||
I11(p) = - |
p2LC(r |
|
+ r |
) + p[C(r |
|
+ r |
)(r |
|
+ r ) + L - Cr2 |
]+ (r |
+ r ) |
, |
|||||
1 |
|
2 |
1 |
|
2 |
1 |
3 |
1 |
1 |
3 |
|
||||||
|
|
pC(r1 + r2 )Li3 (0+) + Li3 (0+) + r1CuC (0+) |
|
|
|
||||||||||||
I22 (p) = |
p2LC(r |
+ r |
) + p[C(r |
+ r |
)(r |
+ r ) + L - Cr2 ] |
+ (r + r ) |
. |
|||||||||
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
3 |
1 |
1 |
3 |
|
|
||
Разделив числитель и знаменатель в двух последних выражениях на LC(r1 + r2 ) и подставив численные значения, получим
I11(p) = - |
|
0,806p + 1693 |
|
, |
||||
p2 |
+18970p + 181×106 |
|
||||||
|
|
|
|
|
||||
I22 |
(p) = |
|
|
0,826p + 13785 |
|
. |
||
p2 + 18970p +181×106 |
||||||||
|
|
|
|
|||||
Ёмкость на операторной схеме замещения цепи изображается операторным сопро- тивлением и источником ЭДС, учитывающим ненулевые начальные условия. По-
этому выражение для операторного напряжения на ёмкости запишется в виде
|
|
U |
|
(p) = |
uC (0+) |
+ |
1 |
I (p) . |
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
C |
|
|
|
p |
pC 11 |
|
||
После подстановки получим |
|
|
|
|
|
|
|
|
|
|
||
U |
|
(p) = |
17,35 |
- |
|
1,493×106p + 3135×106 |
. |
|||||
C |
|
|
p |
|
p(p2 +18970p +181×106 ) |
|||||||
|
|
|
|
|
|
|
||||||
Для перехода от найденных операторных изображений токов и напряжений к ори- гиналам воспользуемся теоремой разложения.
Если изображение по Лапласу искомой зависимости представлено в виде отноше-
ния двух полиномов
F(p) = M(p)N(p) ,
то оригинал находится по выражению
59
PDF created with pdfFactory Pro trial version www.pdffactory.com
f(t) = ån M(pk ) epk ×t , k=1 N¢(pk )
где n – порядок характеристического уравнения;
pk – k -й корень характеристического уравнения N(p)=0; N′(p) – производная полинома N(p) .
Для тока в индуктивности i3(t) запишем:
M(p)=0,826р+13735;
N(p)= p2 +18970p+181×106 ;
N′(p) = 2p + 18970 .
Решая характеристическое уравнение p2 +18970p+181×106 =0, находим два корня
p1 = −9485 + j9525 и p2 = −9485 − j9525. |
|
|
|
|
|
|
|
|
|||
При этом ток в индуктивности i3(t) |
в соответствии с теоремой разложения запи- |
||||||||||
шется в виде |
|
|
|
|
|
|
|
|
|
|
|
|
M(p1) |
|
p |
×t |
|
M(p2 ) |
|
p |
|
×t |
|
i3 (t) = |
|
|
e 1 |
|
+ |
|
e |
|
2 |
|
. |
¢ |
|
|
¢ |
|
|
||||||
|
N (p1) |
|
|
|
N (p2 ) |
|
|
|
|
|
|
Коэффициенты при экспонентах в случае комплексно-сопряжённых корней тоже будут комплексно-сопряжёнными, поэтому при суммировании мнимая часть будет равна нулю и ток i3(t) можно определить как удвоенное значение вещественной
части первого или второго слагаемых.
|
|
é M(p1) |
p |
×t ù |
|
i3 |
(t) = 2Re |
ê |
|
e 1 |
ú . |
¢ |
|||||
|
|
ë N (p1) |
|
û |
|
После подстановки в последнее выражение численных значений получим
i3 |
(t) = 2Re |
é |
0,826(-9485 + j9525) +13735 |
e |
-(9485+ j9525)×t ù |
= |
|
ê |
|
ú |
|||||
2(-9485 + j9525) +18970 |
|||||||
|
|
ë |
|
û |
|
= 1,032e-9485×tsin(9525t + 53,17o)А.
Переходное напряжение на ёмкости вычислим, используя полученное раньше изо- бражение UC (p) и свойство линейности преобразования Лапласа. Сумме изобра-
жений
UC (p) = U1(p) + U2 (p)
будет соответствовать сумма оригиналов
uC (t) = u1(t) + u2 (t) .
60
PDF created with pdfFactory Pro trial version www.pdffactory.com
Введём обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U (p) = 17,35 ;U |
|
(p) = - |
1,493×106p + 3135×106 |
|
|
= |
M(p) . |
|||||||||||||
|
p(p2 +18970p +181×106 ) |
|||||||||||||||||||
1 |
p |
|
2 |
|
|
|
|
N(p) |
||||||||||||
Изображению |
U1(p) в |
области оригиналов |
будет |
соответствовать константа |
||||||||||||||||
u1(t) =17,35. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оригинал u2 (t) |
определим, используя теорему разложения. |
Характеристическое |
||||||||||||||||||
уравнение N(p) = 0 имеет три корня: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p = 0; |
p = −9485+ j9525; |
|
|
|
|
p = −9485− j9525. |
||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M(p1) |
p ×t |
|
M(p2 ) |
|
p |
|
×t |
|
|
M(p3 ) |
|
|
p |
|
×t |
|
||
|
u2 (t) = - |
|
|
|
e 1 |
+ |
|
e |
|
2 |
|
+ |
|
|
e |
|
3 |
|
. |
|
|
¢ |
|
|
¢ |
|
|
|
¢ |
|
|
||||||||||
|
|
N (p1) |
|
|
N (p2 ) |
|
|
|
|
|
|
N (p3) |
|
|
|
|
|
|
||
После подстановки численных значений и выполнения всех преобразований полу-
чим
u2 (t) =141e-9485×tsin(9525t + 173o) −17,35 В.
Складывая u1(t) и u2 (t) , находим полное переходное напряжение на ёмкости uC (t) =141e-9485×tsin(9525t +173o) В.
Длительность переходного процесса равна трём постоянным времени. Постоянная времени определяется как величина, обратная действительной части корня характе- ристического уравнения.
Графики переходных процессов по току в индуктивности i3(t) и по напряжению на ёмкости uC (t) представлены на рис. 4.5 и 4.6 соответственно.
61
PDF created with pdfFactory Pro trial version www.pdffactory.com