
Лабораторная работа №1.
Тема - Численное интегрирование.
Вычислить значение заданного определенного интеграла в пределах от а до b
по формулах левых прямоугольников (вариатнты 0 - 7), правых прямоугольников (варианты 8-15), средних прямоугольников (варианты 16-25)
по формуле трапеций;
по формуле Симпсона;
привести алгоритм, текст программы, вычисленные по ней значения интеграла для метода прямоугольников (четные варианты), метода трапецій (нечетные варианты).
В методе
прямоугольников и Симпсона шаг h,
принять
равным
![]() ,
в
методе трапеций
выбрать такой
шаг, который
бы обеспечивал величину погрешности
вычислений не более 0.01.
,
в
методе трапеций
выбрать такой
шаг, который
бы обеспечивал величину погрешности
вычислений не более 0.01.
Варианты:
0).
![]() 5).
5).
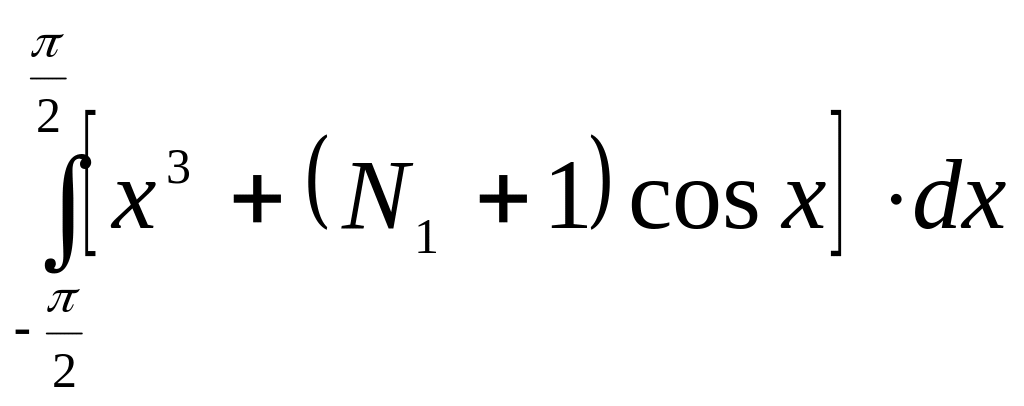
1).
![]() 6).
6).
![]()
2).
![]() 7).
7).
![]()
3).
![]() 8).
8).
![]()
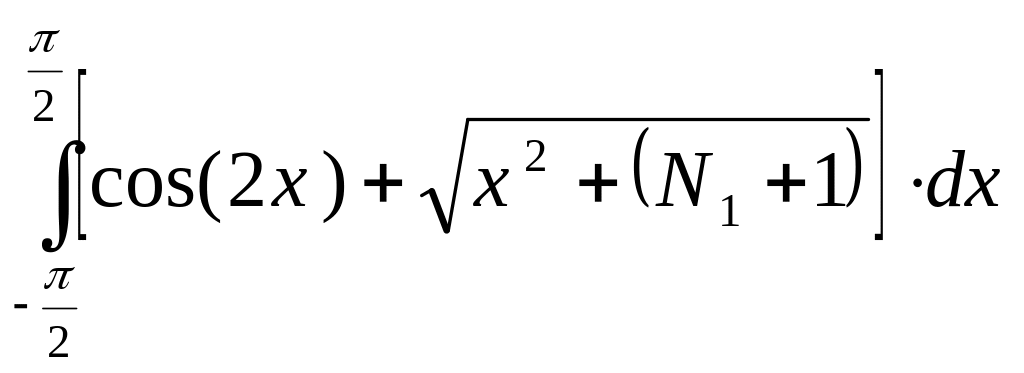
4).
![]() 9).
9).
![]()
Лабораторная работа № 2.
Тема - Интерполирование функций.
Дана функция, заданная таблично:
-
i
0
1
2
3
4
xi
-2
-1
0
1
2
yi
П - N1
N0 - 2
10 - П
12 - N1
N0 - 5
Найти:
коэффициенты интерполирующего полинома и найти его значение при x = (N-20)/10 (для N=10 принять x=0.2, для N=20 принять x=1.2, для N=30 принять x=1.5)
выписать полином Лагранжа в явном виде;
по формулам Лагранжа и Ньютона вычислить значение интерполирующего полинома при том же значении x.
произвести интерполирование этой функции по методу кусочно-линейной интерполяции (привести формулу и график) и вычислить значение при том же значении x
В отчете по работе привести все промежуточные вычисления каждого задания. Расчеты можно производить в Excel или с помощью калькуляторов. Написание программы не предполагается.
Лабораторная работа № 3
Тема - Среднеквадратическое приближение функций.
Для заданных экспериментальных данных (в виде набора пар точек (xi, yi)) подобрать наилучшую (по критерию минимума среднеквадратической невязки) зависимость среди четырех зависимостей, заданных порядковыми номерами из следующего набора зависимостей:
1 |
|
|
9 |
|
2 |
|
|
10 |
|
3
|
|
|
11
|
|
4
|
|
|
12
|
|
5
|
|
|
13 |
|
6
|
|
|
14 |
|
7
|
|
|
15
|
|
8 |
|
|
16 |
a / х2 + b |
Для каждой из этих зависимостей определить
значения коэффициентов;
среднеквадратическое отклонение,
коэффициент детерминации;
относительную ошибку аппроксимации;
выполнить прогноз на следующие два периода.
езультаты привести в следующем виде:
исходные данные
xi
1
2
3

10
yi
линеаризация функций,
результаты приближения по отдельным зависимостям
Формула
a
b
S
R2
а
y = f1(x,a,b)
б
y = f2(x,a,b)
в
y = f3(x,a,b)
г
y = f4(x,a,b)
привести графики исходных данных и получившихся функций,
наиболее хорошо приближает экспериментальные данные зависимость y=???…. с конкретными значениями коеффициентов. Для нее:
-
xi
yi
f(хi)
1
2
……..
-
10
прогноз
11
-
12
-
Варианты:
N / x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Зависимости |
1 |
4,23 |
8,95 |
19,11 |
40,25 |
84,95 |
180,20 |
382,44 |
806,96 |
1708 |
3615 |
1, 2, 10, 11 |
2 |
0,03 |
0,25 |
0,84 |
2,05 |
3,9 |
6,72 |
10,7 |
15,95 |
22,78 |
31,25 |
2, 5, 6, 10 |
3 |
0,16 |
0,28 |
0,42 |
0,48 |
0,59 |
0,65 |
0,72 |
0,79 |
0,85 |
0,92 |
2, 3, 5, 7 |
4 |
0,61 |
0,57 |
0,52 |
0,51 |
0,47 |
0,4 |
0,41 |
0,4 |
0,38 |
0,36 |
1, 4, 6, 5 |
5 |
3,45 |
4,05 |
4,47 |
5,03 |
5,49 |
6,02 |
6,54 |
6,94 |
7,44 |
8,12 |
1, 5, 8, 11 |
6 |
0,22 |
1,62 |
2,41 |
3,02 |
3,46 |
3,82 |
4,12 |
4,4 |
4,62 |
4,83 |
5, 6, 9, 12 |
7 |
0,03 |
0,22 |
0,57 |
0,86 |
0,98 |
0,98 |
0,99 |
0,99 |
0,99 |
0,99 |
6, 7, 10, 12 |
8 |
1,24 |
0,87 |
0,74 |
0,67 |
0,62 |
0,59 |
0,56 |
0,54 |
0,52 |
0,51 |
2, 6, 8, 10 |
9 |
14,12 |
7,98 |
6,05 |
4,95 |
4,41 |
4,01 |
3,71 |
3,51 |
3,33 |
3,21 |
5, 9, 12, 15 |
10 |
3,12 |
3,51 |
4,12 |
4,99 |
6,12 |
7,51 |
9,11 |
10,98 |
13,13 |
15,49 |
1, 8, 10, 11 |
11 |
2,63 |
3,46 |
4,56 |
6,01 |
7,89 |
10,39 |
13,68 |
17,98 |
23,68 |
31,18 |
1, 5, 6, 11 |
12 |
0,0001 |
0,005 |
0,04 |
0,1 |
0,18 |
0,27 |
0,36 |
0,44 |
0,53 |
0,6 |
5, 6, 11, 12 |
13 |
0,47 |
0,43 |
0,39 |
0,35 |
0,31 |
0,27 |
0,23 |
0,19 |
0,16 |
0,13 |
1, 5, 11, 13 |
14 |
0,65 |
0,62 |
0,56 |
0,51 |
0,44 |
0,38 |
0,33 |
0,29 |
0,25 |
0,22 |
1, 5, 13, 14 |
15 |
0,57 |
0,54 |
0,52 |
0,5 |
0,49 |
0,47 |
0,46 |
0,45 |
0,44 |
0,44 |
2, 6, 5, 15 |
16 |
1,65 |
2,72 |
4,48 |
7,39 |
12,18 |
20,09 |
33,11 |
54,59 |
90,02 |
148,4 |
1, 5, 11, 16 |
17 |
0,06 |
0,25 |
0,56 |
1,01 |
1,56 |
2,25 |
3,06 |
3,99 |
5,06 |
6,24 |
2, 6, 10, 16 |
18 |
0,11 |
0,21 |
0,27 |
0,33 |
0,38 |
0,43 |
0,47 |
0,51 |
0,53 |
0,56 |
3, 6, 7, 10 |
19 |
0,44 |
0,41 |
0,36 |
0,33 |
0,31 |
0,29 |
0,27 |
0,25 |
0,24 |
0,22 |
1, 4, 10, 13 |
20 |
2,24 |
2,51 |
2,71 |
2,96 |
3,25 |
3,51 |
3,94 |
3,99 |
4,24 |
4,51 |
1, 5, 11, 15 |
21 |
0,61 |
1,31 |
1,71 |
2,01 |
2,22 |
2,41 |
2,56 |
2,69 |
2,81 |
2,92 |
3, 6, 9, 12 |
22 |
0,06 |
0,22 |
0,43 |
0,63 |
0,79 |
0,89 |
0,95 |
0,98 |
0,99 |
0,99 |
5, 6, 15, 16 |
23 |
1,63 |
0,77 |
0,58 |
0,50 |
0,45 |
0,42 |
0,39 |
0,37 |
0,36 |
0,34 |
2, 8, 9, 12 |
24 |
8,99 |
5,01 |
3,67 |
3,01 |
2,60 |
2,33 |
2,14 |
2,01 |
1,89 |
1,80 |
2, 6, 9, 15 |
25 |
2,06 |
2,25 |
2,56 |
3,01 |
3,56 |
4,25 |
5,06 |
6,01 |
7,06 |
8,25 |
5, 9, 11, 15 |
26 |
1,19 |
1,41 |
1,68 |
2,00 |
2,38 |
2,83 |
3,36 |
4,01 |
4,76 |
5,66 |
1, 5, 11, 14 |
27 |
0,00 |
0,02 |
0,07 |
0,14 |
0,20 |
0,26 |
0,32 |
0,38 |
0,41 |
0,45 |
5, 6, 9, 12 |
28 |
0,31 |
0,27 |
0,24 |
0,21 |
0,18 |
0,15 |
0,13 |
0,11 |
0,09 |
0,07 |
1, 10, 13, 14 |
29 |
0,48 |
0,44 |
0,39 |
0,33 |
0,28 |
0,24 |
0,20 |
0,17 |
0,14 |
0,12 |
5, 6, 7, 14 |
30 |
0,40 |
0,37 |
0,35 |
0,33 |
0,32 |
0,31 |
0,3 |
0,29 |
0,29 |
0,28 |
6, 7, 11, 15 |
