Вариант №1.
Задача №1.
Обработать ряд наблюдений, полученных в результате многократных прямых измерений физической величины (ФВ), и оценить случайную погрешность измерений, считая результаты исправленными и равноточными. Результат измерения представить по одной из форм МИ 1317-86 или ГОСТ 8.207-76. Вид ФВ - ток, ее размерность - мкА, число наблюдений N=20, первый элемент выборки ряда J=1 взять из таблицы по предпоследней цифре шифра зачетной книжки студента, номер ряда взять из таблицы по последней цифре шифра. Доверительную вероятность принять Рд = 0,99 - для нечётных вариантов. Берем из таблицы 1-й ряд и выбираем 20 членов с 1-го по 20-й включительно.
Решение: Таблица 1.
|
i |
Xi |
Vi |
Vi2 |
|
1 |
22,0123 |
-0.4362 |
0.1903 |
|
2 |
22,9939 |
0.5454 |
0.2975 |
|
3 |
22,2742 |
-0.1743 |
0.0304 |
|
4 |
23,0254 |
0.5769 |
0.3328 |
|
5 |
22,3024 |
-0.1461 |
0.0213 |
|
6 |
22,0120 |
-0.4365 |
0.1905 |
|
7 |
22,8651 |
0.4166 |
0.1736 |
|
8 |
22,3795 |
-0.0690 |
0.0048 |
|
9 |
22,7172 |
0.2687 |
0.0722 |
|
10 |
22,8255 |
0.3770 |
0.1421 |
|
11 |
22,4244 |
-0.0241 |
5.7985e-4 |
|
12 |
20,0291 |
-2.4194 |
5.8534 |
|
13 |
22,7570 |
0.3085 |
0.0952 |
|
14 |
22,3292 |
-0.1193 |
0.0142 |
|
15 |
22,9448 |
0.4963 |
0.2463 |
|
16 |
22,0760 |
-0.3725 |
0.1387 |
|
17 |
23,0105 |
0.5620 |
0.3159 |
|
18 |
22,0643 |
-0.3842 |
0.1476 |
|
19 |
23,0317 |
0.5832 |
0.3401 |
|
20 |
22,8951 |
0.4466 |
0.1995 |
Так как в условии задачи указано, что результаты измерения являются исправленными и равноточными, то производить исключение систематических погрешностей нет необходимости.
Вычислим среднее арифметическое результатов наблюдений:
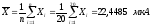
Значение
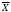 принимается за результат измерения.
принимается за результат измерения.
Определим
случайные отклонения
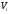 результатов отдельных наблюдений.
результатов отдельных наблюдений.
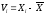
Результаты занесем в таблицу 1.
Правильность
вычислений
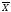 и
и
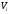 определяем по формуле
определяем по формуле
 .
Если
.
Если
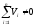 ,
то имеют место ошибки в вычислениях.
,
то имеют место ошибки в вычислениях.
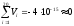
Вычислим
оценку среднего квадратичного отклонения
результатов наблюдений
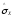 .
.
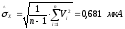
С
помощью критерия грубых погрешностей
(критерий «трех сигм») проверяем наличие
грубых погрешностей. Если
 ,
то такое наблюдение содержит грубую
погрешность и его необходимо исключить.
,
то такое наблюдение содержит грубую
погрешность и его необходимо исключить.
В
задаче
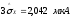 ,
и из таблицы 1 видно, что наблюдение №12
содержит грубую погрешность и его
необходимо исключить.
,
и из таблицы 1 видно, что наблюдение №12
содержит грубую погрешность и его
необходимо исключить.
Таблица 2.
|
i |
Xi |
Vi |
Vi2 |
|
1 |
22,0123 |
-0.5635 |
0.3176 |
|
2 |
22,9939 |
0.4181 |
0.1748 |
|
3 |
22,2742 |
-0.3016 |
0.0910 |
|
4 |
23,0254 |
0.4496 |
0.2021 |
|
5 |
22,3024 |
-0.2734 |
0.0748 |
|
6 |
22,0120 |
-0.5638 |
0.3179 |
|
7 |
22,8651 |
0.2893 |
0.0837 |
|
8 |
22,3795 |
-0.1963 |
0.0385 |
|
9 |
22,7172 |
0.1414 |
0.0200 |
|
10 |
22,8255 |
0.2497 |
0.0623 |
|
11 |
22,4244 |
-0.1514 |
0.0229 |
|
12 |
22,7570 |
0.1812 |
0.0328 |
|
13 |
22,3292 |
-0.2466 |
0.0608 |
|
14 |
22,9448 |
0.3690 |
0.1361 |
|
15 |
22,0760 |
-0.4998 |
0.2498 |
|
16 |
23,0105 |
0.4347 |
0.1890 |
|
17 |
22,0643 |
-0.5115 |
0.2616 |
|
18 |
23,0317 |
0.4559 |
0.2078 |
|
19 |
22,8951 |
0.3193 |
0.1019 |
Так как в условии задачи указано, что результаты измерения являются исправленными и равноточными, то производить исключение систематических погрешностей нет необходимости.
Вычислим среднее арифметическое результатов наблюдений:
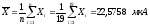
Значение
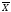 принимается за результат измерения.
принимается за результат измерения.
Определим
случайные отклонения
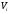 результатов отдельных наблюдений.
результатов отдельных наблюдений.
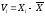
Результаты занесем в таблицу 2.
Правильность
вычислений
 и
и
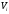 определяем по формуле
определяем по формуле
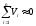 .
Если
.
Если
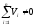 ,
то имеют место ошибки в вычислениях.
,
то имеют место ошибки в вычислениях.
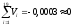
Вычислим
оценку среднего квадратичного отклонения
результатов наблюдений
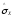 .
.
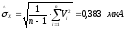
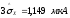 ,
и из таблицы 2 видно, что грубые погрешности
отсутствуют.
,
и из таблицы 2 видно, что грубые погрешности
отсутствуют.
Определим
оценку среднего квадратического
отклонения результата измерения
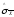 :
:

Критерий 1. Вычисляем смещённую оценку среднего квадратического отклонения по формуле
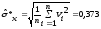 мкА.
мкА.
Вычисляем параметр
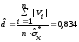 .
.
Результаты наблюдений можно считать распределенными нормально, если
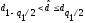 ,
,
где
 и
и
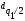 - квантили распределения.
- квантили распределения.
Выбираем
уровень значимости q равным 1 %. Из таблицы
находим
 =
0,900,
=
0,900,
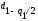 =
0,695. Сравнивая полученное значение
=
0,695. Сравнивая полученное значение
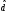 с этими величинами, делаем вывод о том,
что по критерию 1 результаты наблюдений
распределены по нормальному закону.
с этими величинами, делаем вывод о том,
что по критерию 1 результаты наблюдений
распределены по нормальному закону.
Критерий 2. Этот критерий используется дополнительно для проверки «концов» распределений.
Гипотеза
о нормальности по критерию 2 не отвергается,
если не более m разностей Vi
превзошли значение
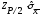 ,
где верная квантиль распределения
нормированной функции Лапласа отвечает
вероятности P/2.
,
где верная квантиль распределения
нормированной функции Лапласа отвечает
вероятности P/2.
Для решаемой задачи выбираем уровень значимости q2 = 1% и для n = 19 P = 0,99 и m = 1. Тогда находим ZP/2 = 2,58. Отсюда
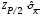 =
0,988 мкА.
=
0,988 мкА.
Согласно критерию 2 не более (m = 1) разности Vi могут превзойти значение 0,988 мкА.
По данным, приведенным в таблице 2, видим, что ни одно V не превышает критическое значение. Следовательно, критерий 2 выполняется.
Таким образом, с уровнем значимости q q1+ q2 = 0,1 гипотеза о нормальности полученных данных согласуется с данными наблюдений.
По заданной доверительной вероятности РД=0,99 и числу степеней свободы (n-1)=18 распределения Стьюдента определим коэффициент t:
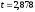
Рассчитаем границы случайной погрешности результата измерения:
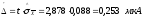
Запишем результат измерения:
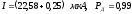
Задача №2.
Необходимо определить доверительные границы суммарной погрешности результата измерения и записать его по МИ 1317-86 или ГОСТ 8.207-76. Значение доверительной вероятности принять Рд= 0,99 для нечетных вариантов. При расчетах полагать, что случайные погрешности распределены по нормальному закону, а число наблюдений существенно больше 30.
В
процессе обработки результатов прямых
измерений напряжения U
определено (все значения в вольтах):
среднее арифметическое
 ,
среднее квадратическое отклонение
результата измерения
,
среднее квадратическое отклонение
результата измерения
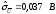 ,
границы неисключенных остатков двух
составляющих систематической погрешности
,
границы неисключенных остатков двух
составляющих систематической погрешности
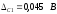 и
и
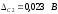 .
.
Решение:
Рассчитываем доверительные границы случайной погрешности результата измерения:
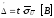
Для РД=0,99 и n>30 коэффициент Стьюдента t=2,576 [2]. Тогда
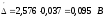 .
.
Определим доверительные границы неисключенной систематической погрешности результата измерения:

где m − число суммируемых погрешностей;
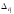 − граница
i-ой неисключенной погрешности;
− граница
i-ой неисключенной погрешности;
к − коэффициент, определяемый принятой доверительной вероятностью.
При
доверительной вероятности Рд
= 0,99 коэффициент k принимают равным 1,4,
если число суммируемых неисключенных
систематических погрешностей более
четырёх (m >4). Если число суммируемых
погрешностей m4,
то коэффициент k определяют по графику
зависимости (рисунок) k=f(m, l), где m - число
суммируемых погрешностей;
 ;
кривая 1 - для m =2; кривая 2 - для m = 3; кривая
3 - для m = 4.
;
кривая 1 - для m =2; кривая 2 - для m = 3; кривая
3 - для m = 4.
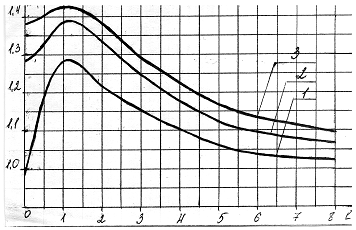
График зависимости k = f(m, l).
При
трёх или четырёх составляющих в качестве
 принимают составляющую, по числовому
значению наиболее отличающуюся от
других. В качестве
принимают составляющую, по числовому
значению наиболее отличающуюся от
других. В качестве
 следует принять ближайшую к
следует принять ближайшую к
 составляющую.
составляющую.
Для
нашей задачи
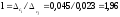 .
.
Используя первую кривую графика, находим k = 1,22.
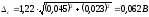
Вычислим алгебраическую сумму систематических погрешностей:
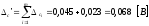
За
оценку неисключенной систематической
погрешности принимаем то из значений
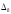 ,
которое меньше. Таким образом,
,
которое меньше. Таким образом,
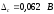 .
.
Найдем
отношение:
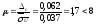 .
.
Значит, граница погрешности результата будет [2]:
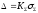 ,
,
Где
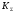 – коэффициент, зависящий от соотношения
случайной и неисключенной систематической
погрешностей.
– коэффициент, зависящий от соотношения
случайной и неисключенной систематической
погрешностей.
 – оценка
суммарного среднего квадратического
отклонения результата измерения.
– оценка
суммарного среднего квадратического
отклонения результата измерения.
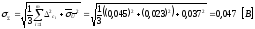
Коэффициент
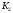 вычисляют по эмпирической формуле:
вычисляют по эмпирической формуле:
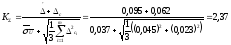
Определим доверительные границы суммарной погрешности результата измерения:
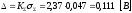
Запишем результат измерения:
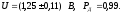
Задача №8.
Необходимо определить доверительные границы суммарной погрешности результата измерения и записать его по МИ 1317-86 или ГОСТ 8.207-76. Значение доверительной вероятности принять Рд = 0,99 для нечётных вариантов. При расчётах полагать, что случайные погрешности распределены по нормальному закону, а число наблюдений существенно больше 30.
В
процессе обработки результатов прямых
измерений индуктивности катушки L
определено: среднее арифметическое
 мГн; границы неисключенных остатков
двух составляющих систематической
погрешности
мГн; границы неисключенных остатков
двух составляющих систематической
погрешности
 мГн,
мГн,
 мГн. Случайная погрешность пренебрежимо
мала.
мГн. Случайная погрешность пренебрежимо
мала.
Определим доверительные границы неисключенной систематической погрешности результата измерения:
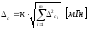 ,
,
где m − число суммируемых погрешностей;
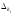 − граница
i-ой неисключенной погрешности;
− граница
i-ой неисключенной погрешности;
к − коэффициент, определяемый принятой доверительной вероятностью.
При
доверительной вероятности Рд
= 0,99 коэффициент k принимают равным 1,4,
если число суммируемых неисключенных
систематических погрешностей более
четырёх (m >4). Если число суммируемых
погрешностей m4,
то коэффициент k определяют по графику
зависимости (рисунок) k=f(m, l), где m - число
суммируемых погрешностей;
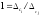 ;
кривая 1 - для m =2; кривая 2 - для m = 3; кривая
3 - для m = 4.
;
кривая 1 - для m =2; кривая 2 - для m = 3; кривая
3 - для m = 4.
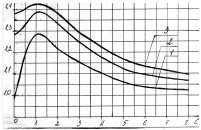
График зависимости k = f(m, l).
При
трёх или четырёх составляющих в качестве
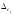 принимают составляющую, по числовому
значению наиболее отличающуюся от
других. В качестве
принимают составляющую, по числовому
значению наиболее отличающуюся от
других. В качестве
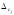 следует принять ближайшую к
следует принять ближайшую к
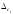 составляющую.
составляющую.
Для
нашей задачи
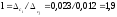 .
.
Используя вторую кривую графика, находим k = 1,23.

Вычислим алгебраическую сумму систематических погрешностей:
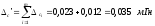
За
оценку неисключенной систематической
погрешности принимаем то из значений
 ,
которое меньше. Таким образом,
,
которое меньше. Таким образом,
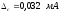 .
.
Запишем результат измерения: