
Теория норм синдромов
.docxЗадание 1.
По построенной в задании 8 из КР «Прикладная математика» двоичной проверочной (10х31) – матрице Н реверсивного кода, найти порождающую (21х31) – матрицу G этого кода.
Решение задания 1.
При
помощи элементарных преобразований
строк матрицы НR,
приведем ее к виду
 .
Здесь
.
Здесь
 – единичная
матрица порядка n
- k.
– единичная
матрица порядка n
- k.




Из
полученной матрицы
 составим порождающую матрицу
составим порождающую матрицу
 :
:

Задание 2.
С
помощью найденной порождающей матрицы
закодировать информацию
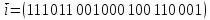 .
.
Решение задания 2.
Кодовое слово по данному информационному вектору
 вычисляется
по формуле:
вычисляется
по формуле: .
Получим
следующий вектор
.
Получим
следующий вектор
 :
:

Задание 3.
По
найденному в задании 2 кодовому слову
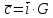 попытаться восстановить сообщение
попытаться восстановить сообщение
 .
.
Решение задания 3.
В
силу структуры матрицы G
информационный вектор
 идентично отображается на последние
21 координатe
вектора
идентично отображается на последние
21 координатe
вектора
 и, следовательно, однозначно
восстанавливается по вектору
и, следовательно, однозначно
восстанавливается по вектору
 .
Вектор
.
Вектор
 записан в последних 21 координатах
вектора
записан в последних 21 координатах
вектора
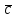 .
.
Задание 4.
По найденному в задании 9 (Вариант 10) из КР «Прикладная математика» синдрому найти вектор ошибок сведением задачи к квадратному уравнению и решением последнего по формулам Чэня.
Решение задания 4.
В указанном задании 9, на основе кода с проверочной матрицей НR из решённого выше задания 1 приняло сообщение:
 .
.
Наличие
ошибок в принятом сообщении
 было определено вычислением синдрома
H
·
было определено вычислением синдрома
H
·
 =
S.
Оказалось, что в данном случае:
=
S.
Оказалось, что в данном случае:
S
= H
·
 =
(1001110000)T
≠
=
(1001110000)T
≠
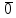 .
.
Приведём таблицу из решения задания 9, задающую поле Галуа GF(32).
|
α |
α |
(00010) |
|
α2 |
α2 |
(00100) |
|
α3 |
α3 |
(01000) |
|
α4 |
α4 |
(10000) |
|
α5 |
α4 + α2 + α + 1 |
(10111) |
|
α6 |
α4 + α3 + 1 |
(11001) |
|
α7 |
α2 + 1 |
(00101) |
|
α8 |
α3 + α |
(01010) |
|
α9 |
α4 + α2 |
(10100) |
|
α10 |
α4 + α3 + α2 + α + 1 |
(11111) |
|
α11 |
α3 + 1 |
(01001) |
|
α12 |
α4 + α |
(10010) |
|
α13 |
α4 + α + 1 |
(10011) |
|
α14 |
α4 + 1 |
(10001) |
|
α15 |
α4 + α2 + 1 |
(10101) |
|
α16 |
α4 + α3 + α2 + 1 |
(11101) |
|
α17 |
α3 + α2 + 1 |
(01101) |
|
α18 |
α4 + α3 + α |
(11010) |
|
α19 |
α + 1 |
(00011) |
|
α20 |
α2 + α |
(00110) |
|
α21 |
α3 + α2 |
(01100) |
|
α22 |
α4 + α3 |
(11000) |
|
α23 |
α2 + α + 1 |
(00111) |
|
α24 |
α3 + α2 + α |
(01110) |
|
α25 |
α4 + α3 + α2 |
(11100) |
|
α26 |
α3 + α2 + α + 1 |
(01111) |
|
α27 |
α4 + α3 + α2 + α |
(11110) |
|
α28 |
α3 + α + 1 |
(01011) |
|
α29 |
α4 + α2 + α |
(10110) |
|
α30 |
α4 + α3 + α + 1 |
(11011) |
|
α31 |
1 |
(00001) |
В
соответствии со структурой матрицы НR
данный
синдром S
разбивается
на компоненты s1
=
(10011)
и s2
=
(10000).
Сравнивая
эти компоненты с данными таблицы,
задающей поле Галуа GF(32),
получаем: s1
=
α13;
s2
=α4.
(31,
21) реверсивного кода с рассматриваемой
проверочной матрицей НR
исправляет
одиночные и двойные ошибки в принимаемых
сообщениях. Если бы сообщение
 содержало
одиночную ошибку, то тогда имело бы
место равенство:
содержало
одиночную ошибку, то тогда имело бы
место равенство:
 ,
что, очевидно, не выполняется.
,
что, очевидно, не выполняется.
Для определения координат двойной ошибки составим систему уравнений:

Левую
часть второго уравнения приведём к
общему знаменателю, то есть к виду:
 .
.
Получим
 ;
;

По
теореме Виета х
и
y
являются
корнями квадратного уравнения:
 Произведем замену: t
= α13
· z.
Произведем замену: t
= α13
· z.
Тогда:
 ,
,
 ,
,
 .
.
След
 .
Поэтому
наше квадратное уравнение обязательно
имеет корни в поле GF(32).
.
Поэтому
наше квадратное уравнение обязательно
имеет корни в поле GF(32).
Методом
Чэня, то есть последовательной
подстановкой элементов αi,
 ,
в квадратное уравнение, находим корни
этого уравнения α3
и
α11.
Теперь найдем х
и у:
,
в квадратное уравнение, находим корни
этого уравнения α3
и
α11.
Теперь найдем х
и у:
t1 = α13 · z1 = α13 · α3 = α16 = x; t2 = α13 · z2 = α13 · α11 = α24 = y.
Действительно, f(α16) = α32+α13·α16+α9 = 0;
f(α24) = α48+α13·α24+α9 = 0.
Следовательно,
двойная ошибка произошла на 17-й и 25-й
позициях, то есть вектор-ошибка
 и
истинным является сообщение:
и
истинным является сообщение:
 .
.
Задание 5.
Для
рассматриваемого в задании 4 кода
составить таблицу образующих
 Г-орбит двойных ошибок, синдромов
Г-орбит двойных ошибок, синдромов
 и норм
и норм
 .
По синдрому ошибки из задания 4 найти
вектор-ошибку норменным методом.
.
По синдрому ошибки из задания 4 найти
вектор-ошибку норменным методом.
Решение задания 5.
Составим
таблицу векторов ошибок
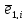 на позициях 1 и
i,
2
≤ i
≤ 16, образующих
Г-орбит
на позициях 1 и
i,
2
≤ i
≤ 16, образующих
Г-орбит
 ,
двойных
ошибок, показателей
,
двойных
ошибок, показателей
 и
и
 синдромов
синдромов
 ,
где
,
где
 и
показателей
и
показателей
 ,
норм синдромов
,
норм синдромов
 .
.
|
Г-орбита
|
Образующая
|
|
|
|
|
|
(1, 2) |
19 |
18 |
6 |
|
|
(1, 3) |
7 |
5 |
12 |
|
|
(1, 4) |
11 |
8 |
19 |
|
|
(1, 5) |
14 |
10 |
24 |
|
|
(1, 6) |
29 |
24 |
22 |
|
|
(1, 7) |
22 |
16 |
7 |
|
|
(1, 8) |
2 |
26 |
28 |
|
|
(1, 9) |
28 |
20 |
17 |
|
|
(1, 10) |
15 |
6 |
21 |
|
|
(1, 11) |
27 |
17 |
13 |
|
|
(1, 12) |
3 |
23 |
26 |
|
|
(1, 13) |
13 |
1 |
14 |
|
|
(1, 14) |
12 |
30 |
11 |
|
|
(1, 15) |
4 |
21 |
25 |
|
|
(1, 16) |
9 |
25 |
3 |
Вычислим
норму синдрома принятого сообщения:
N=α13·α4=α17.
Сравнивая
вычисленную норму с данными таблицы,
находим, что
 .
Следовательно, двойная вектор-ошибка
.
Следовательно, двойная вектор-ошибка
 ,
которая присутствует в
сообщении
,
которая присутствует в
сообщении
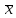 ,
принадлежит Г-орбите J9
=<
,
принадлежит Г-орбите J9
=< >
и получается циклическим сдвигом
вектора
>
и получается циклическим сдвигом
вектора
 .
Величина циклического сдвига определяется
отношением первой компоненты
.
Величина циклического сдвига определяется
отношением первой компоненты
 синдрома
синдрома
 к первой компоненте
к первой компоненте
 =α28
синдрома
=α28
синдрома
 .
В данном случае
.
В данном случае
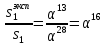 .
Следовательно, искомая ошибка
.
Следовательно, искомая ошибка
 –
вектор-ошибка весом 2 с
единицей
на 17-й и 25-й позициях, что полностью
совпадает с полученным ранее решением
задания 4.
–
вектор-ошибка весом 2 с
единицей
на 17-й и 25-й позициях, что полностью
совпадает с полученным ранее решением
задания 4.
Задание 6.
В
(31, 16) БЧХ-коде C7
с проверочной матрицей
 где α– корень примитивного полинома
p(x)
= x5
+ x4
+ x2
+ x
+ 1, принято сообщение
где α– корень примитивного полинома
p(x)
= x5
+ x4
+ x2
+ x
+ 1, принято сообщение
 с синдромом S
= S(
с синдромом S
= S( )
= (
)
= (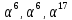 ).
Найти вектор ошибок в принятом сообщении
сведением задачи к кубическому уравнению
и решением этого уравнения методом
Чэня.
).
Найти вектор ошибок в принятом сообщении
сведением задачи к кубическому уравнению
и решением этого уравнения методом
Чэня.
Решение задания 6.
Тройная
ошибка в сообщении
 произошла на неизвестных позициях i,
j,
k,
1≤ i
< j
< k
≤
31. В подматрице
произошла на неизвестных позициях i,
j,
k,
1≤ i
< j
< k
≤
31. В подматрице
 матрицы
матрицы
 позициям
i,
j,
k,
соответствуют столбцы
позициям
i,
j,
k,
соответствуют столбцы
 .
Эти столбцы называют локаторами ошибочных
позиций. Их рассматриваем как элементы
поля Галуа GF(32),
задаваемые с
помощью
полинома p(x)=x5+x4+x2+x+1.
Синдром S
= S(
.
Эти столбцы называют локаторами ошибочных
позиций. Их рассматриваем как элементы
поля Галуа GF(32),
задаваемые с
помощью
полинома p(x)=x5+x4+x2+x+1.
Синдром S
= S( )
= (
)
= ( )
получается
двоичным сложением столбцов матрицы
)
получается
двоичным сложением столбцов матрицы
 с
номерами
i,
j,
k.
Каждый
с
номерами
i,
j,
k.
Каждый
 -й
столбец матрицы Н
состоит
из трёх частей, интерпретируемых как
элементы x,
х3,
х5
поля
GF(24).
Поэтому
для определения истинных значений
позиций
i,
j,
k,
искомой
тройной ошибки мы с помощью синдрома S
= S(
-й
столбец матрицы Н
состоит
из трёх частей, интерпретируемых как
элементы x,
х3,
х5
поля
GF(24).
Поэтому
для определения истинных значений
позиций
i,
j,
k,
искомой
тройной ошибки мы с помощью синдрома S
= S( )
= =(
)
= =( )
получаем
следующую систему уравнений:
)
получаем
следующую систему уравнений:

Левые
части уравнений системы (1) есть
симметрические степенные полиномы f1,
f3,
f5
от трёх переменных x,
y,
z.
Здесь
 .
У нас, в условиях двоичной арифметики,
.
У нас, в условиях двоичной арифметики,
 .
В теории
симметрических
полиномов существуют формулы Ньютона,
которые связывают степенные симметрические
полиномы с элементарными симметрическими
полиномами
.
В теории
симметрических
полиномов существуют формулы Ньютона,
которые связывают степенные симметрические
полиномы с элементарными симметрическими
полиномами
 .
Элементарные симметрические полиномы
от трёх переменных x,
у, z
выглядят
следующим образом:
.
Элементарные симметрические полиномы
от трёх переменных x,
у, z
выглядят
следующим образом:

В
полях характеристики 2 формулы
Ньютона, связывающие
 c
c
 имеют
специальный вид:
имеют
специальный вид:

Подставим
в систему (2) значения из системы (1):
 .
Получим следующую систему линейных
уравнений относительно неизвестных
.
Получим следующую систему линейных
уравнений относительно неизвестных
 :
:

Подставим
в (3) значения
 .
Получим систему:
.
Получим систему:

Отсюда
следует
 (4)
(4)
Из
первого уравнения системы выражаем
 ,
и подставив во второе, имеем:
,
и подставив во второе, имеем:

Подставим
 в первое уравнение системы (4):
в первое уравнение системы (4):

Полученные
значения
 служат,
согласно теореме Виета, коэффициентами
кубического уравнения
служат,
согласно теореме Виета, коэффициентами
кубического уравнения
 ,
корнями которого и являются искомые в
системе (1) неизвестные x,
у, z.
,
корнями которого и являются искомые в
системе (1) неизвестные x,
у, z.
Итак,
решение системы (1) сводится к поиску
корней кубического уравнения
 в
поле GF(32).
в
поле GF(32).
Метод
Чэня, то есть последовательная подстановка
в уравнение элементов поля GF(32)
вместо
 ,
позволяет найти следующие его корни:
,
позволяет найти следующие его корни:
 .
Корни
однозначно указывают тройную ошибку
на 8-й, 12-й и 16-й позициях в сообщении
.
Корни
однозначно указывают тройную ошибку
на 8-й, 12-й и 16-й позициях в сообщении
 .
.
Задание 7.
Задачу из задания 6 решить норменным методом.
Решение задания 7.
В
двоичном коде длиной 31 имеется 4495 тройных
ошибок, которые делятся на 145 Г-орбит.
Чтобы избежать построения таблицы в
145 строк, модифицируем норменный метод,
преобразуем искомую вектор-ошибку
 в
другую тройную ошибку
в
другую тройную ошибку
 ,
синдром которой имеет первую компоненту
,
синдром которой имеет первую компоненту
 .
Пусть x,
y,
z
– локаторы
ошибочных позиций вектора
.
Пусть x,
y,
z
– локаторы
ошибочных позиций вектора
 ,
ненулевых координат вектора-ошибки
,
ненулевых координат вектора-ошибки
 .
В
качестве
.
В
качестве
 берём
вектор-ошибку весом 3 с локаторами
ненулевых позиций
берём
вектор-ошибку весом 3 с локаторами
ненулевых позиций
 .
Тогда
компоненты синдрома
.
Тогда
компоненты синдрома
 выражаются
следующим образом через компоненты
синдрома
выражаются
следующим образом через компоненты
синдрома
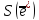 :
:





 .
.
У
нас S
= S( )
= (
)
= ( ).
Следовательно:
).
Следовательно:
 .
.
Таким
образом
 =
(
=
( ).
Тогда
).
Тогда
 .
.
Известно,
что в (31, 16) БЧХ-коде С7
имеется
в точности 5 Г-орбит тройных ошибок с
первой компонентой синдрома, равной
нулю. Составим таблицу образующих
 этих орбит, синдромов S(
этих орбит, синдромов S( )
и норм синдромов
)
и норм синдромов
 .
.
|
№ п/п i |
|
S( |
|
|
1 |
(1, 2, 20) |
(0, α20, α12) |
(∞, ∞, α29) |
|
2 |
(1, 3, 8) |
(0, α9, α24) |
(∞, ∞, α27) |
|
3 |
(1, 4, 12) |
(0, α14, α18) |
(∞, ∞, α15) |
|
4 |
(1, 5, 15) |
(0, α18, α17) |
(∞, ∞, α23) |
|
5 |
(1, 6, 30) |
(0, α3, α14) |
(∞, ∞, α27) |
Как
видим,
 .
Следовательно,
.
Следовательно,
 получается циклическим сдвигом вектора
получается циклическим сдвигом вектора
 (1,
5, 15). S(
(1,
5, 15). S( )
= (0,
α19,
α29)
=
)
= (0,
α19,
α29)
=
 .
Значит,
.
Значит,
 – тройная
вектор-ошибка с ненулевыми координатами
на 22-й, 26-й, 5-й позициях, локаторы которых
– тройная
вектор-ошибка с ненулевыми координатами
на 22-й, 26-й, 5-й позициях, локаторы которых


 .
Отсюда находятся локаторы x,y,z
ненулевых
координат искомого вектора ошибок
.
Отсюда находятся локаторы x,y,z
ненулевых
координат искомого вектора ошибок
 :
:


 .
.
Следовательно,
 –
тройная ошибка на 8-й, 12-й и 16-й позициях,
что полностью совпадает с решением
задания 6.
–
тройная ошибка на 8-й, 12-й и 16-й позициях,
что полностью совпадает с решением
задания 6.






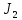



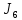





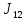




 )
)