Билет 30
Полиномиальная сводимость и np –полные задачи.
Пусть задан граф
G=(V,
E).
V={
,
... ,
},
E
– множество рёбер.
Говорят, что
последовательность вершин графа
образует гамильтонов цикл (ГЦ), если
существуют все рёбра
.
Например, для
графа, изображенного на рис.4.3, существует
гамильтонов цикл
,
показанный пунктиром.
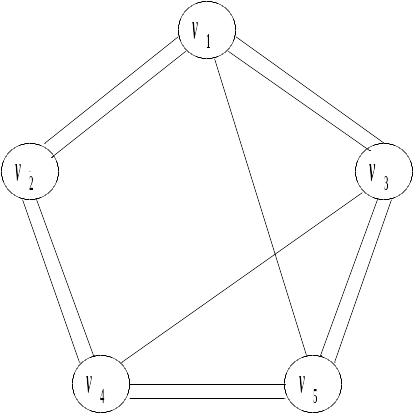
Рис.2.3. Граф G и гамильтонов цикл.
Поставим задачу распознавания гамильтонова цикла: “Пусть задан граф G=(V, E). Верно ли, что G содержит гамильтонов цикл?”
Видна связь между этой задачей и задачей k2.
Говорят, что задача 1 полиномиально сводится к задаче 2, если существует функция преобразования f из класса P, преобразующая постановку задачи 1 в постановку задачи 2.
В данном случае функция, сводящая задачу распознавания гамильтонова цикла к задаче k2, f(ГЦ®k2), строится так:
Множество городов C совпадает с V; для любых двух городов
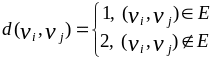
Граница B=n.
Для графа, показанного на предыдущем рисунке, эти преобразования можно проиллюстрировать следующим образом (рис.4.4):
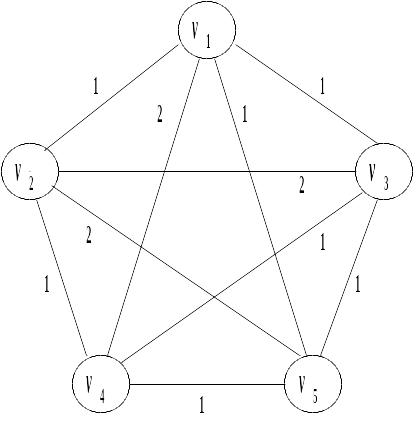
Рис.2.4. Задача коммивояжера.
Очевидно, что подразумеваемая функция f вычисляется за полиномиальное время.
Задачу k2 также можно свести к задаче распознавания гамильтонова цикла: ищется гамильтонов цикл с ограниченным по длине маршрутом. Значит, эти задачи эквивалентны по сложности.
Если задача А полиномиально сводится к задаче В, а задача В – к задаче С, то и задача А полиномиально сводится к задаче С.
Тогда можно теоретически построить класс так называемых NP-полных задач, к каждой из которых сводятся другие задачи из этого же класса.
Рассмотренная сводимость поясняет стратегию выбора решений сложных задач на основе их сведения к задачам, для которых известны эффективные алгоритмы решения.
И если бы удалось хоть одну NP-полную задачу свести к полиномиальной, то и все другие NP-полные задачи свелись бы к полиномиальной.
Уточним гипотетическую модель NP-сложных задач (рис. 4.5).
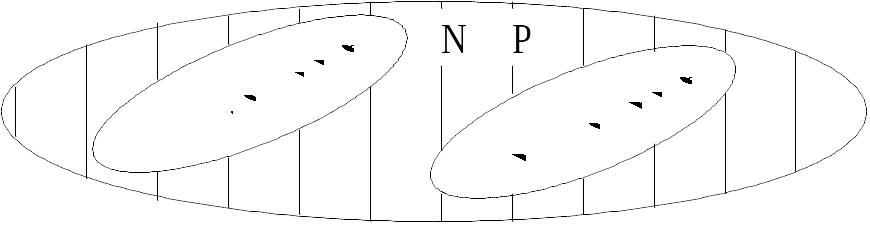
Рис.2.5. Класс сложности NP, P-сложные и NP-полные задачи.
Выше мы выделили в класс NP только задачи распознавания. Но ранее говорили о более широкой категории задач – переборных задачах, которые столь же трудны (теоретически, а практически – даже значительно труднее), что и NP-полные задачи.
Переборная задача в отличие от задачи распознавания, выдающей ответ “да” – “нет”, выдает одно решение, если оно существует. Т.е. для задачи k1 выдаёт длину маршрута минимальной длины. Принято NP-сложные задачи перебора относить к NP-трудным.
Сюда же относятся задачи перечисления, выдающие все возможные решения при переборе (практически они ещё более сложны).
Можно показать полиномиальную сводимость NP-трудной задачи k1 к NP-полной задаче k2. А именно, заменим в (2) знак нестрогого неравенства “£” на знак “<“. Иными словами, мы будем проверять вновь полученный маршрут имеет ли он меньшую, чем В длину. Если “да”, то меняем В на длину вновь найденного маршрута. Таким образом, далее мы будем искать ещё более короткий маршрут и т.д. По окончании всех “угадываний” зафиксируется минимальный по длине маршрут.
Итак, последняя гипотетическая модель NP-сложных задач выглядит следующим образом (рис. 4.6):
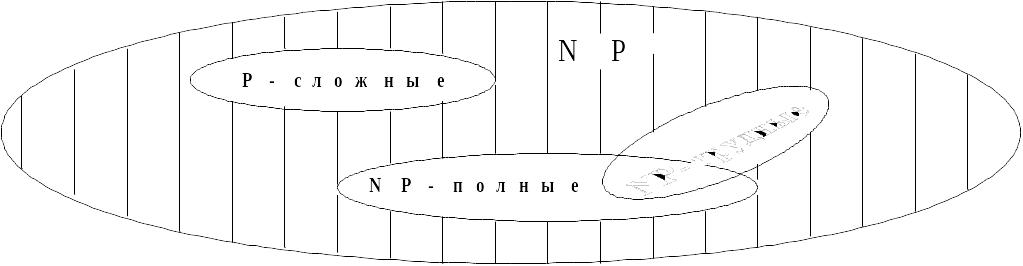
Рис.2.6. Наиболее полная модель NP-сложных задач.