Билет 28

1. Сложность итерационных и рекурсивных алгоритмов.

Отнесём к итерационным алгоритмам и те, к которым сводятся рекурсивные алгоритмы (например, вычисление факториала n!). Тогда время их выполнения (в случае сходящегося процесса) зависит от главного условия повторения итерации, например, от требуемой точности. Если мы установим время или сложность одной итерации, то сможем умножением на число итераций установить максимальную или среднюю сложность. Число итераций устанавливается теоретически или экспериментально. Например, так можно сделать при расчете значений функций по их разложению в ряд.

Однако иногда приходится решать оптимизационную задачу, выбирая между сложностью одной итерации и количеством итераций. Например, при решении системы дифференциальных уравнений в частных производных методом сеток (конечно-разностным методом).

Пусть решается уравнение в частных производных:

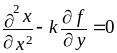
Его решение f(x, y) ищется в области 0£x£A, 0£y£B

На границах области заданы граничные условия

Область задания функции – решения f(x, y) покрывают сеткой с шагом h_x по оси x и шагом h_y по оси y. Ищутся дискретные значения функции – решения в узлах этой сетки, f_{i, j}.

Частные производные всех порядков могут быть приближенно выражены (разными способами) через конечные разности – с помощью значений функции в соседних узлах. Воспользуемся одним из таких способов:

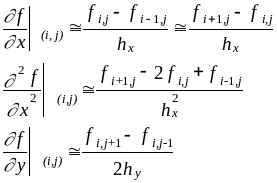
Подставим эти соотношения в решаемое уравнение:

и разрешим его относительно f_i,j. Получим рекуррентное соотношение для нахождения приближенного значения функции f(x, y) в узле (i, j) через значения в четырех соседних узлах (напомним, что на границах значения f уже заданы):

f _{i, j} = 0.5( f _{i+1, j} + f _{i–1, j} ) – a( f _{i, j+1} – f _{i, j–1} ), где

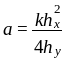
От итерации к итерации рассчитываем значение функции f во всех узлах до тех пор, пока эти значения в каждом узле не перестанут изменяться вне пределов заданной точности.

Можно считать, что сложность одной итерации O( ) или O(n´m), где – количество узлов при равном разбиении по x и по y, а n´m – то же количество при различающемся разбиении по осям. Увеличение количества узлов, покрывающих ту же область, т.е. уменьшение h_x и h_y увеличивает скорость сходимости – и, соответственно, уменьшает число итераций, но сложность каждой итерации растет квадратично. Значит, необходим компромисс, который достигается посредством изучения поведения процесса как на теоретическом, так и на экспериментальном уровне, вплоть до автоматической коррекции шагов в процессе вычислений в зависимости от локального поведения аппроксимаций производных. Т.е. шаги становятся непостоянными во всей области.

Однако по своей природе действительно рекурсивные алгоритмы по сложности относятся к классу экспоненциальных алгоритмов. Как правило, это задачи оптимизации, основанные на переборе (алгоритмы с возвратом, метод “ветвей и границ”).

Имеется широко распространенное соглашение, по которому задача не считается “хорошо решаемой”, пока для нее не получен полиномиальный алгоритм. Задача называется труднорешаемой, если для ее решения не существует полиномиального алгоритма.

Эта градация относительна, ибо сложность определяется по наихудшему варианту. Хотя реализация метода “ветвей и границ” – труднорешаемая задача (при теоретической оценке по максимальной сложности), сейчас для многих задач известны такие алгоритмы, которые практически очень быстро находят решение именно методом ветвей и границ.

Однако есть понятие гарантированных и негарантированных оценок. Если сложность задачи полиномиальная, мы можем уверенно предсказать оценку времени решения. При решении задачи методом “ветвей и границ” незначительное изменение начальных данных даже без изменения размерности задачи может непредсказуемо привести к резкому скачку во времени решения. Т.е. существует большой разрыв между значениями теоретической максимальной сложности и практической средней сложности экспоненциальных алгоритмов. Постоянно ведутся поиски более эффективных экспоненциальных алгоритмов.