Билет 29
Классы сложности.
Казалось бы, мы завершили классификацию, разложив все алгоритмы на два класса: полиномиальных и экспоненциальных. Однако современные исследователи пытаются проникнуть в суть экспоненциальных алгоритмов, выделить там основные категории, произвести более детальную классификацию, вскрыть отношения между классами. Т.к. понятия этой классификации широко используются в литературе, мы кратко на них остановимся.
Полиномиальные по сложности алгоритмы относят к классу P-сложных. Среди экспоненциальных выделяют алгоритмы, основанные на переборе, и их выделяют в класс NP-сложных (т.е. формально возможно существование экспоненциальных алгоритмов, основанных не на переборе. Например, n!, растущий быстрее, чем ). К NP-сложным относятся, например, задачи линейного целочисленного программирования, составление расписания, поиск кратчайшего пути в лабиринте и т.д. Обратим внимание, что все это дискретные задачи.
Например, булевская задача о рюкзаке:
Ее можно решить,
перебирая булевские n-мерные
векторы-варианты. Число вариантов равно
.
Т.е. при больших n
задача труднорешаемая, а далее, с учетом
ограниченных возможностей вычислительных
средств – практически неразрешимая.
Но к классу NP
относятся и неразрешимые задачи,
например, десятая проблема Гильберта:
“Существует ли алгоритм, который по
данному полиному p(
,
... ,
)
c целыми коэффициентами распознает,
имеет ли уравнение p=0
решение в целых числах”. Доказано, что
такого алгоритма в принципе не существует,
хотя можно методом перебора попытаться
решить эту задачу. Если ограничиться
областью поиска | xi
|£X,
то сложность
его составляет
.
Классическая
задача о коммивояжере (k1):
Есть конечный набор городов C={
,
,
... ,
}
и расстояний
между ними d(
,
).
Необходимо
найти упорядоченный набор этих городов
такой, что
(1)
Т.е. надо найти путь обхода всех n городов (без повторного посещения) минимальной длины.
Это NP-сложная задача; поиск решения требует проверки n! перестановок n городов. Сложность задачи O(n!) (еще раз напомним, что n! растет быстрее, чем ). При этом (см. пример на рис. 4.1) не обязательно выполняется правило треугольника:
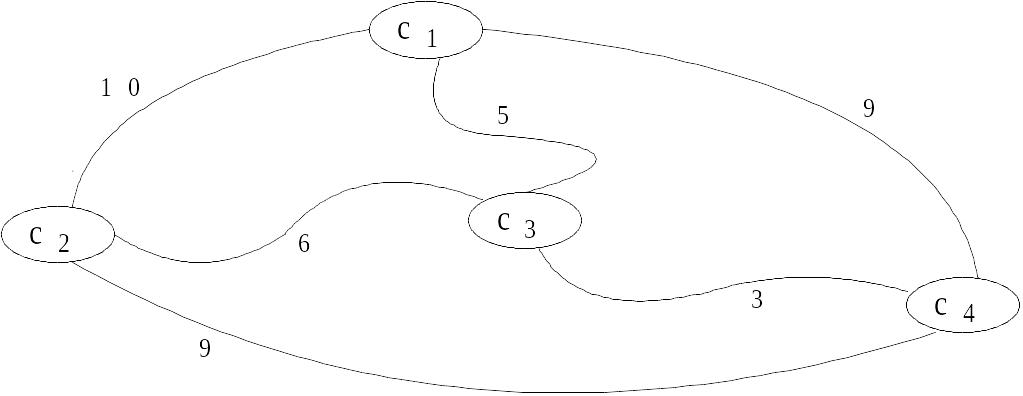
Рис.2.1. Задача о коммивояжере.
Проиллюстрированная
конкретная задача имеет решение <
,
,
,
,>, определяющее минимально возможный
маршрут длиной 27.
Выделим в классе NP-сложных задач задачи распознавания свойств, которые имеют два решения – “да” или “нет”.
Видоизменим задачу о коммивояжере (т.е. сформулируем задачу k2):
Условие:
Задано множество городов C={
,
... ,
}
и расстояний d(ci,
cj)
между ними, а также граница В
длины маршрута обхода городов.
Вопрос:
Существует ли маршрут, проходящий через
все города из C,
длина которого не превосходит В?
Т.е. существует ли перестановка
такая, что
(2)
Будем исходить из того очевидного факта, что задачи распознавания обладают той же сложностью, что и задача оптимизации (k1); поэтому выводы о сложности второй задачи применимы и к задачам оптимизации.
Можно представить следующую схему решения задачи распознавания свойств на примере задачи k2 :
1. Предъявление некоторого маршрута (стадия угадывания).
2. Проверка: является ли он решением, т.е. соответствует ли условиям задачи, а по длине – не превосходит B. Т.е. определение ответа – “да” или “нет” (стадия проверки).
Очевидно, что процедуру проверки можно представить алгоритмом полиномиальной временной сложности. Стадия же угадывания порождает экспоненциальную сложность. Такие алгоритмы, состоящие из указанных двух стадий, называют недетерминированными.
Отсюда – класс NP определяется как класс всех задач типа распознавания, которые могут быть решены недетерминированными (N – nondeterministic) алгоритмами за полиномиальное (P – polinomial) время.
Тогда все алгоритмы класса P можно считать подмножеством множества NP, или детерминированными алгоритмами. Тогда гипотетическая картина класса NP-сложных задач может быть представлена таким образом (рис. 4.2):
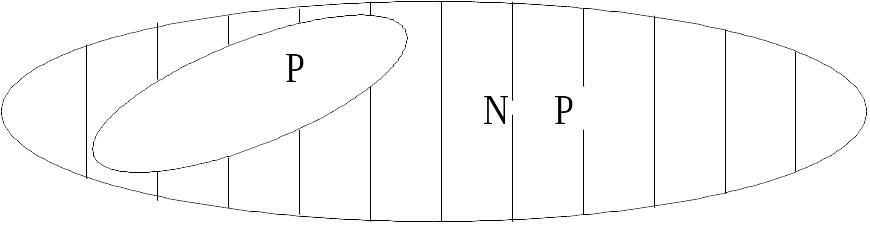
Рис.2.2. Классы сложности NP и P.