§27. Обобщённый закон Ома.

I. Сторонние силы.

Сторонняя электродвижущая сила совершает положительную работу по перемещению положительного заряда в сторону возрастания потенциала, т.е. против сил электростатического поля (вследствие сопротивления потенциал электростатического поля понижается, положительный заряд двигается от большего потенциала к меньшему => должны существовать участки, на которых “+” заряд движется от меньшего потенциала к большему ).

Сторонняя сила не может иметь электростатического происхождения т.к. электростатическое поле — потенциальное и А по замкнутому пути =0 и ток не мог бы существовать, т.к. он должен совершать работу для преодоления сопротивления проводника.

Физическая природа сторонних сил весьма различна:

Они могут быть обусловлены:

а) химической, физической неоднородностью проводника при соприкосновении разнородных проводников (гальванические элементы; аккумуляторы—возникает контактная разность потенциалов при контакте твёрдого тела и жидкости)

б) физическая неоднородность при соприкосновении проводников различной температуры ( термоэлементы)

в) механические происхождения

г) электрическое происхождение — сила действует на заряд в электростатическом поле , возникающем по закону электромагнитной индукции.

II. Обобщённый закон Ома.

Для количественной характеристики сторонних сил вводя понятие поле сторонних сил и его напряжённости. - численно равный сторонней силе, действующей не единичный пробный положительный заряд.

Под совместным действием поля ив проводнике возникает ток плотности:

обобщённый закон Ома в дифференциальной форме.

Рассмотрим неоднородный участок цепи , на котором действуют сторонние силы. Предположим электрический ток течёт вдоль тонких проводов ( направление тока совпадает с направлением от провода j=constпоS) (Рис. 80)

Рис. 80

, т.к. тонкий.

Проинтегрируем по длине провода от 1 до 2

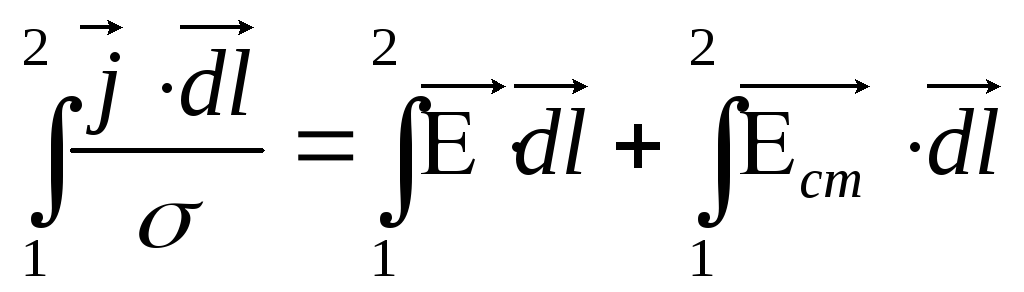( где , а)

-электродвижущая сила (ЭДС)действующая на участки 1—2 ,величина алгебраическая. Если ЭДС способствует движению положительных носителей тока>0, препятствует<0.

R₁₂*I=₁ -- ₂ + -интегральная форма обобщенного закона Ома для неоднородного 0участка цепи.

Замечание:

1. Для замкнутой цепи =

*R_i=-закон Ома для замкнутой цепи.

R_i -полное сопротивление замкнутой цепи

-алгебраическая сумма отдельных ЭДС

2. Р

   1

   2

   ассмотрим участок цепи, содержащий источник

Если источник разомкнут I=0 и

=--ЭДС источника – разность потенциалов на его клемах в разомкнутом состоянии. При замкнутом источнике на внешнее сопротивление (нагрузку)-<и зависит отR_внеш

Расчет линейных цепей постоянного тока. Правила Кирхгофа

Линейные цепи линейная связь между разностью потенциалов и током. Для них справедливы прав. Кирхгофа. Они образуют систему уравнений, позволяющую рассчитать любую разветвленную электр. цепь.

1-е правило Кирхгофа:

Алгебраическая сумма токов для узла = 0

Количество независ. Уравнений, составляемых по первому правилу Кирхгофа = количество узлов –1

1-е правило - есть из закона зарядов.

2-е правило:

Для замкнутого контура

Количество независимых уравнений, составленных по 2-му правилу Кирхгофа = количеству неделимых контуров

Применение правила К-а:

1) Определяем количество ветвей в эл. схеме (ветвь – участок эл. схемы между соседними узлами). Количество токов = количеству ветвей

2) Определяем количество узлов и записываем для них 1-ое прав. Кирхгофа.

3) Определяем количество неделимых контуров и запис. IIпр. Кирхгофа, выбрав направление обхода по каждому контуру.

рис.81

4) Решаем систему лин. уравнений и анализируем ответ. Если ток получился со знаком “-”Þнаправление тока противоположно выбранному обх.

Пример Найти токи в электрической цепи (рис.81)

Дано:

e_i,, R_i

_______

I_i - ?

1. 3 ветви Þ 3 тока: I₁, I₂, I₃

2. 2 узла Þ1-е ур-ие поIпр.I₁ + I₂ + I₃ = 0

3. 2 независ. контура Þ2-е ур-ие поIIпр.

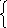Е₁ – Е₃ = I₁R₁ - I₃ R₃

Е₂ + Е₃ = -I₂R₂ + I₃ R₃

Решить дома эту систему.