
контрольная работа по физике в4
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного и дистанционного обучения
Специальность: информационные технологии и управление в технических системах
Контрольная работа по физике №5
Вариант № x4
Пилипенко Олега Валерьевича
Группа №702421
зачётная книжка №702421-14
Электронный адрес: skidel@tut.by
504. В опыте Юнга расстояние между щелями 0,8 мм, а экран от щелей находится за 2,5 м. Найти ширину интерференционной полосы. Как изменится ее ширина, если экран приблизить на 1 м?
|
Дано: d = 0,8 мм = 8·10-4 м l = 2,5 м l1 = 1 м |
Р
|
|
Найти: Δh – ? Δh1 – ? |
Ширина интерференционной полосы – это расстояние между двумя соседними светлыми или темными интерференционными полосами
Разность хода двух лучей. попадающих в точку наблюдения Δ = s1 – s2
Как видно из чертежа,
![]() ,
отсюда Δ =
,
отсюда Δ =
![]()
Так как угол α мал, то Cosα ≈ 1.
Тогда Δ =
![]() (1)
(1)
Светлые интерференционные полосы наблюдаются на экране в тех местах, где разность хода двух волн равна четному числу полуволн (или целому числу длин волн):
Δ = 2k![]() = kλ
(k
= 0, ±1, ±2, …) (2)
= kλ
(k
= 0, ±1, ±2, …) (2)
Приравняем правые части (1) и (2):
![]() = kλ
= kλ
Отсюда hk
=
![]()
Для (k
+1)-го максимума hk+1
=
![]()
Δh
= hk+1
– hk
=
![]() –
–
![]() =
=
![]()
Δh
=
![]()
Δh1
=
![]()
Ответ:
ширина интерференционной полосы зависит
от длины волны λ,
которая в условии задачи не задана. Δh
=
![]() ;
Δh1
=
;
Δh1
=
![]() .
.
514. Между пластинкой и лежащей на ней плосковыпуклой линзой с радиусом кривизны R = 0,5 м находится жидкость. Найти показатель преломления жидкости, если радиус третьего темного кольца Ньютона в отраженном свете с длиной волны λ = 700 нм равен 0,82 нм.
|
Дано: R = 0,5 м λ = 700 нм = 7·10-7 м r3 = 0,82 нм = 8,2·10-10 м k = 3 |
Р
|
|
Найти: n – ? |
Оптическая разность хода Δ волн 1 и 2, отраженных от верхней и нижней поверхностей водяного клина, образованного поверхностями линзы и пластинки, складывается из разности оптических длин путей этих волн 2dnCos r (n – показатель преломления вещества клина, r – угол преломления; в нашем случае свет падает нормально, угол преломления r = 0; d – толщина клина в том месте, где наблюдается интерференция) и дополнительной разности хода λ/2, возникающей при отражении волны 2 от оптически более плотной среды:
Δ = 2dnCos
r
+
![]() = 2dn
+
= 2dn
+
![]() (1)
(1)
Минимумы интенсивности наблюдаются на тех участках клина, для которых оптическая разность хода равна нечетному число полуволн:
Δ = (2k
+ 1)![]() (2)
(2)
Приравнивая правые части (1) и (2):
2dn
+
![]() = (2k
+ 1)
= (2k
+ 1)![]()
2dn
+
![]() = 2k
= 2k![]() +
+
![]()
2dn = kλ
Отсюда
n
=
![]() (3)
(3)
Из рисунка видно, что
R2 = (R – d)2 + rk2
R2 = R2 – 2dR + d2 + rk2
Пренебрегая d2 как величиной второго порядка малости по сравнению с 2Rd, получим 2dR = rk2.
Отсюда 2d
=
![]()
Подставив в (3):
n
=
![]() –
расчетная
формула
–
расчетная
формула
Проверка размерности:
[n]
=
![]() = 1.
= 1.
n
=
![]() = 1,6·1012
= 1,6·1012
Этот ответ нереален.
Предположим, что r3 = 0,82 мм = 0,82·10-3 м = 8,2·10-4 м.
n
=
![]() = 1,6
= 1,6
Ответ: n = 1,6.
524. Какое наименьшее число штрихов должна иметь дифракционная решетка с периодом d = 5 мкм, чтобы в спектре второго порядка были видны раздельно две линии натрия λ1 = 589 нм и λ2 = 589,6 нм? Какова длина такой решетки?
|
Дано: d = 5мкм = 5·10-6 м λ1 = 589 нм λ2 = 589,6 нм K = 2 |
Решение Число штрихов N дифракционной решетки связано с ее разрешающей силой R и порядком спектра K соотношением: R = KN, отсюда
N
=
Минимальному значению Nmin соответствует мини- |
|
Найти: Nmin – ? L– ? |
мальное значение Rmin:
Nmin
=
![]() (1)
(1)
Минимальная разрешающая сила решетки Rmin, необходимая двух линий с длинами волн λ1 и λ2:
Rmin
=
![]()
Подставив в (1):
Nmin
=
![]()

Число штрихов дифракционной решетки на единицу длины решетки n, связано с периодом решетки d как
n
=
![]()
Длину решетки L можно найти, разделив число штрихов во всей решетке N на число штрихов, приходящееся на единицу длины n:
L
=
![]() = Nd
= Nd
Lmin
= Nmind
=
![]()
Lmin
=
![]()

Nmin
=
![]() = 491
= 491
Lmin
=
![]() = 2454·10-6(м)
≈ 2,5 мм.
= 2454·10-6(м)
≈ 2,5 мм.
Ответ: Nmin = 491; Lmin ≈ 2,5 мм.
534. В пластинке толщиной 1 мм плоскость поляризации для света длиной волны 471 нм поворачивается на угол 21,72о. Найти разность показателей преломления Δn кварца для лево- и правополяризованного света.
|
Дано: d = 1 мм = 10-3м λ = 471 нм = 4,71·10-7 м φ = 21,72о |
Решение При прохождении пути d в оптически активном веществе угол поворота плоскости поляризации
φ
=
|
|
Найти: Δn – ? |
Δn– разности показателей преломления для лево- и правополяризованного света.
Отсюда Δn
=
![]()
Необходимо перевести угол в радианы:
360о = 2π
21,72о
=
![]() = 0,12π
= 0,12π
Δn
=
![]() = 5,66·10-5.
= 5,66·10-5.
Ответ: Δn = 5,66·10-5.
544. Пластинка кварца толщиной 1,2 мм вращает плоскость поляризации красного света (λ = 700 нм) на угол 11о. На какой угол повернет плоскость поляризации пластинка с толщиной 3,6 мм для света с той де длиной волны?
|
Дано: d1 = 1,2 мм λ = 700 нм φ1 = 11о d2 = 3,6 мм |
Решение Угол поворота φ плоскости поляризации оптически активными твердыми веществами φ = αd где α – постоянная вращения. Для 1-й пластинки: φ1 = αd1 |
|
Найти: φ2 – ? |
Отсюда α
=
![]()
Для 2-й пластинки:
φ2
= αd2
=
![]() d2
d2
φ2
= φ1![]()
φ2
= 11·![]() = 33о
= 33о
Ответ: φ2 = 33о.
554. Абсолютно черное тело находится при температуре Т = 3900 К. При остывании длина волны, на которую приходится максимум плотности энергии, изменилась на Δλ = 0,3 мкм. До какой температуры Т2 охладилось тело?
|
Дано: Т = 3900 К = 3,9·103 К Δλ = 0,3 мкм = 3·10-7 м |
Решение Закон смещения Вина: длина волны, на которую приходится максимум энергии излучения, обратно пропорциональна термодинамической температуре |
|
Найти: Т2 – ? |
λmax
=
![]()
b – постоянная закона смещения Вина; b = 2,9·10-3 м·К.
Для температуры
Т2
: λ2max
=
![]()
Δλ
= λ2max
– λmax
=
![]() –
–
![]()
Отсюда
![]() =
=
![]() + Δλ
=
+ Δλ
=
![]()
Т2
=
![]()
Т2
=
![]() = 2779 К.
= 2779 К.
Ответ: Т2 = 2779 К.
564. На металлическую пластину направлен пучок ультрафиолетового излучения λ = 0,25 мкм. Фототок прекращается при минимальной задерживающей разности потенциалов U = 96 В. Определить работу выхода А электронов из металла и красную границу фотоэффекта.
|
Дано: λ = 0,25 мкм = 2,5·10-7 м U = 96 В |
Решение Уравнение Эйнштейна для фотоэффекта: hν = A + Tmax (1)
где hν
=
|
|
Найти: А – ? λmax – ? |
h – постоянная Планка; h = 6,63∙10-34 Дж∙с;
с
– скорость света в вакууме; с
= 3∙108
![]() .
.
A – работа выхода электрона из металла;
Tmax – максимальная кинетическая энергия электрона.
Фототок
прекращается. когда между катодом и
анодом приложена задерживающая разность
потенциалов U
=
![]() .
е
– заряд электрона; е
= 1,6·10-19
Кл.
.
е
– заряд электрона; е
= 1,6·10-19
Кл.
Tmax = eU
Подставив в (1):
![]() = A
+ еU
= A
+ еU
Отсюда A
=
![]() – еU. (2)
– еU. (2)

Красная граница
фотоэффекта – это такая длина волны
падающего на поверхность металла света,
при которой энергии фотона
![]() достаточно только для совершения работы
выхода электрона из металла, а кинетическая
энергия фотоэлектронов Tmax
= 0. В случае красной границы уравнение
Эйнштейна для фотоэффекта запишется:
достаточно только для совершения работы
выхода электрона из металла, а кинетическая
энергия фотоэлектронов Tmax
= 0. В случае красной границы уравнение
Эйнштейна для фотоэффекта запишется:
![]() = A
= A
Отсюда
λmax
=
![]() =
=
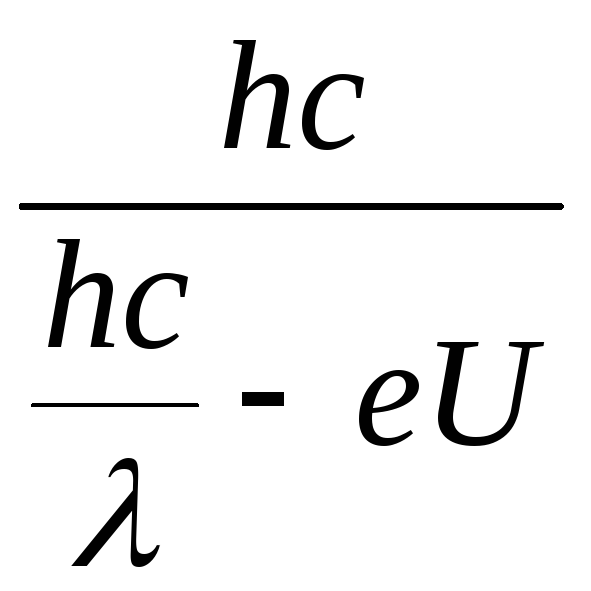 =
=
![]()
λmax
=
![]()

A
=
![]() = 7,96·10-19
– 153,6·10-19.
= 7,96·10-19
– 153,6·10-19.
Полученный отрицательный ответ не имеет смысла. Результат реален при U = 0,96 В:
A
=
![]() = 7,96·10-19
– 1,54·10-19
= 6,42·10-19(Дж).
= 7,96·10-19
– 1,54·10-19
= 6,42·10-19(Дж).
Такое значение работы выхода соответствует табличному значению для цинка.
λmax
=
![]()
λmax
=
![]() = 3,10·10-7
(м)
= 3,10·10-7
(м)
Ответ: A = 6,42·10-19 Дж; λmax = 3,10·10-7 м.
574.Фотон с энергией
1,27 МэВ падает на металл Cu
и вызывает фотоэффект. Найти скорость
фотоэлектронов и β
=
![]() .
.
|
Дано: ε = 1,27 МэВ |
Решение Уравнение Эйнштейна для фотоэффекта: ε = A + Tmax (1) где ε – энергия фотона, падающего на поверхность металла; |
|
Найти: v – ? β – ? |
Tmax – максимальная кинетическая энергия электрона.
A – работа выхода электрона из металла; работа выхода электрона с поверхности металла составляет единицы электрон-вольт и является пренебрежимо малой по сравнению с энергией фотона: A << ε
Формулу (1) можем записать: ε = Tmax (2)
Кинетическая энергия фотоэлектрона Tmax = ε = 1,27 МэВ сравнима по размеру с энергией покоя электрона Е0, поэтому кинетическую энергию фотоэлектрона необходимо выражать по релятивистской формуле:
Tmax
= (m
– m0)c2
или Tmax
= m0c2![]() = Е0
= Е0![]() ,
(3)
,
(3)
где m0 – масса покоя электрона; m0 = 9,11·10-31 кг;
m – масса релятивистского электрона, движущегося со скоростью v;
с
– скорость света в вакууме; с
= 3∙108
![]() ;
;
Е0 – энергией покоя электрона; Е0 = 0,511 МэВ.
Отсюда
![]() =
=
![]()
![]() =
=
![]() + 1 =
+ 1 =
![]()
![]() =
=
![]()
1
–
![]() =
=
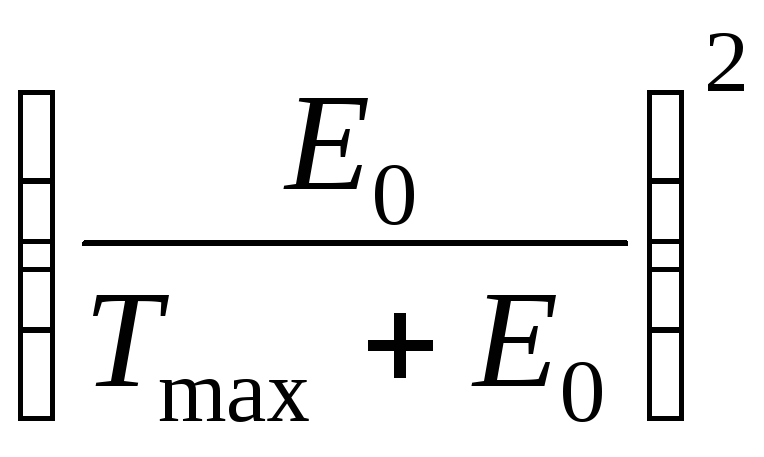
![]() =
1 –
=
1 –
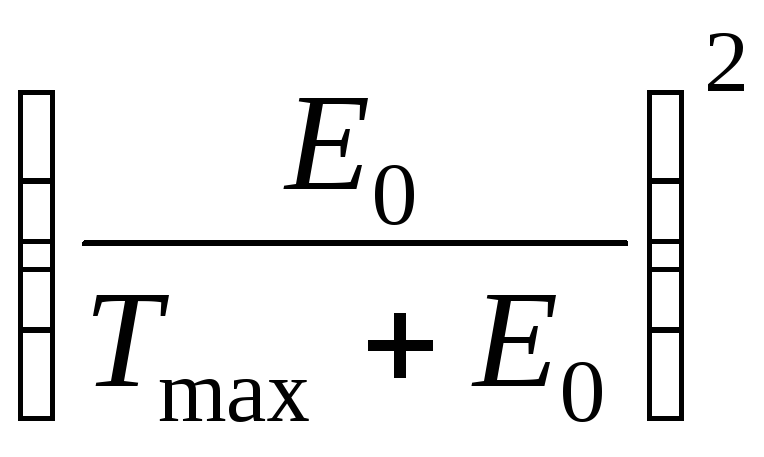 (4)
(4)
β
=
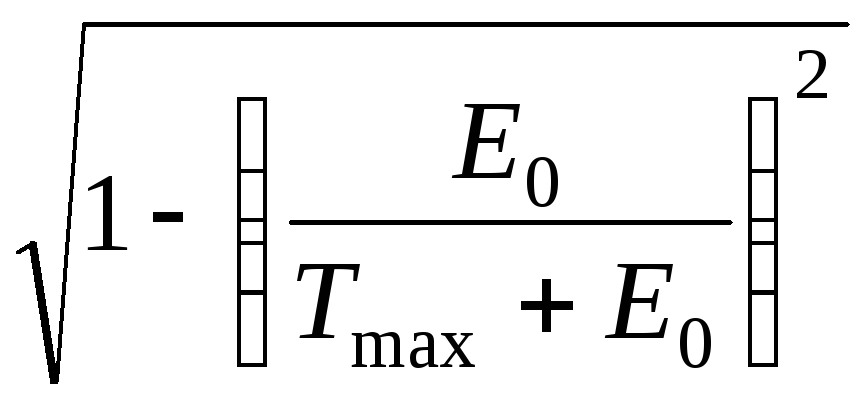
Tmax
=ε, β
=
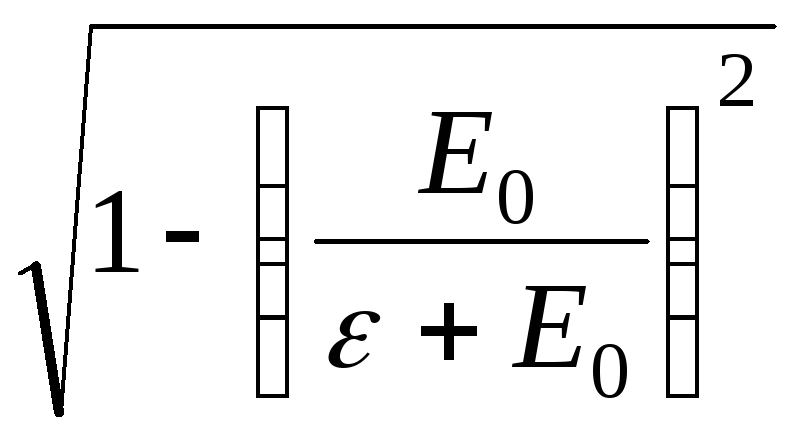 (5)
(5)
Можно преобразовать (4) след. образом.
![]() =
1 –
=
1 –
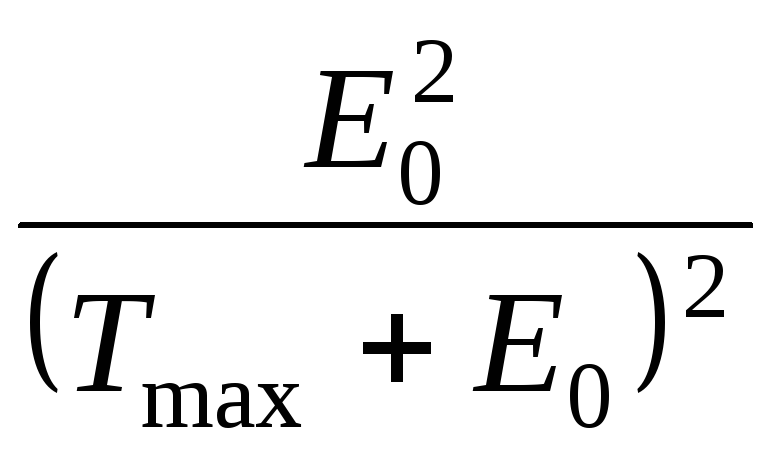 =
=
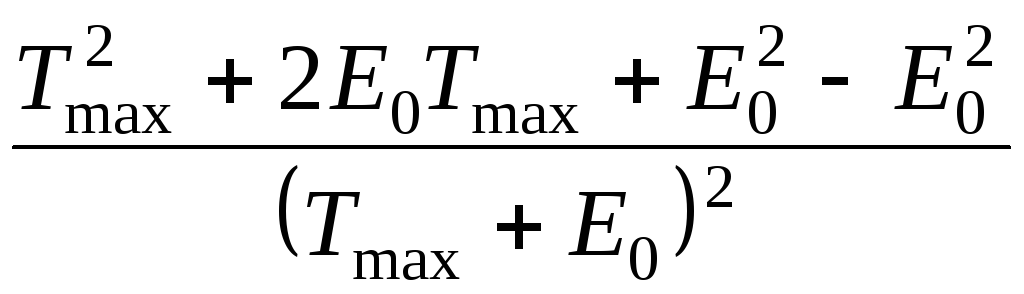 =
=

β
=
![]()
С
учетом (2): β
=
![]() (6)
(6)

v = cβ
v
= c·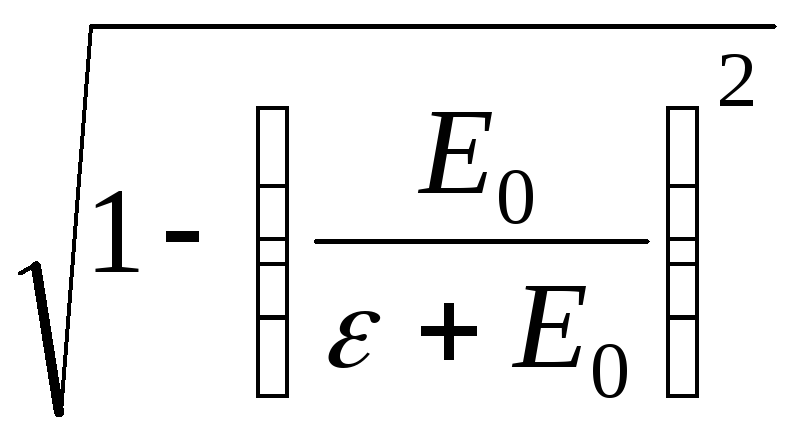 (7)
(7)

или
v
= c·![]() (8)
(8)

Будем производить вычисления по формулам (5) и (7).
β
=
![]() ≈ 0,96.
≈ 0,96.
v
= 3·108.![]() ·≈
2,87·108
·≈
2,87·108
![]()
Ответ:
β
= 0,96; v
= 2,87·108
![]() .
.

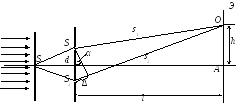 ешение
ешение ешение
ешение