Линейная и круговая поляризации

Наиболее важны два частных случая, когда эллипс поляризации вырождается либо в прямую, либо в окружность.

Согласно и эллипс переходит в прямую при

.

Тогда , и мы говорим олинейнойполяризации.

Н

δ

δ

δ

δ

δ

π/2

π/2

π/2

π/2

π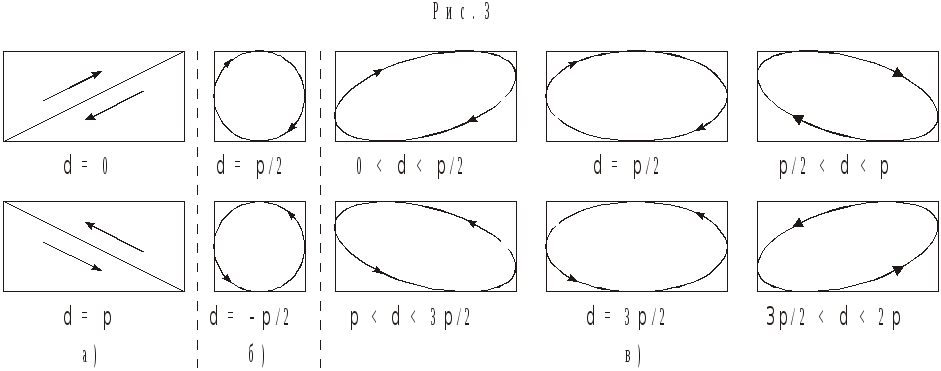

а рис. 1.9, а показаны два возможных направления поляризации в плоско поляризованной волне, соответствующие= 0 и=.

δ

δ

δ

δ

δ

-π/2

3π/2

3π/2

3π/2

π

π

π

Р и с. 1.9

Другой важный случай  случай круговой поляризации волны, когда эллипс вырождается в круг. Необходимое условие этого вырождения заключается в превращении описанного прямоугольника в квадрат, т.е. амплитуды двух взаимно перпендикулярных компонент электрического поля должны быть равными

.

Кроме того, одна из компонент должна равняться нулю, когда другая достигает максимального значения. Отсюда следует, согласно (1.37) и (1.38), что

и уравнение переходит в уравнение окружности

.

В случае правойполяризацииsin > 0, так что

,

,

где .

В случае левойполяризацииsin< 0, так что

,

,

где

.

Из формул и следует, что

.

Это означает, что сумма право- и лево- поляризованных волн дает линейно поляризованную волну.

Если вместо вещественного представления воспользоваться комплексным, т.е. вместо косинусов в и использовать экспоненциальные функции

и,

то .

Из этого отношения сразу же можно определить характер поляризации:

а) Линейная поляризация

.

б) Правая круговая поляризация электрической волны

,

.

в) Левая круговая поляризация

,

.

В более общем случае можно показать, что для правой эллиптической поляризации мнимая часть отношения E_y/E_xположительна, тогда как для левой эллиптической поляризации она отрицательна.

На рис. 1.9, б показана круговая поляризация, на рис. 1.9, в эллипсы поляризации при разных значениях.

Параметры Стокса. Сфера Пуанкаре

Как уже отмечалось, для определения эллипса поляризации необходимы три независимые величины, например амплитуды E₁₀, E₂₀и разность фазили малая и большая осиa,bи угол, характеризующий ориентацию эллипса. Для практических целей состояние поляризации удобно задавать некоторыми параметрами, обладающими одинаковой физической размерностью. Такие параметры были введены Стоксом, и для любой волны их можно определить из простых экспериментов.

Для плоской монохроматической волны параметрами Стокса служат четыре величины.

Лишь три из них независимы, так как справедливо тождество

.

Очевидно, что параметр S₀пропорционален интенсивности волны. ПараметрыS₁, S₂, S₃простым образом связаны с углом, характеризующим ориентацию эллипса, и углом, характеризующим эллиптичность и направление вращения. Справедливы следующие соотношения:

.

Например, последнее из уравнений можно получить, используя ранее записанные соотношения:

,

,

,

,

и тригонометрические формулы

.

Следовательно, .

Выражения подсказывают простое геометрическое представление различных состояний поляризации: S₁, S₂, S₃можно рассматривать как декартовы координаты точкиPна сферерадиусаS₀, причем 2и 2являются сферическими угловыми координатами этой точки (рис. 1.10). Каждому возможному состоянию поляризации плоской монохроматической волны заданной интенсивности (S₀=const) соответствует одна точка на сфере, и наоборот.

Так как угол (или sin(2)) положителен или отрицателен в зависимости от того, имеем ли мы дело с правой или левой поляризацией, то из последнего уравнения соотношений следует, что правая поляризация представляется точками на, лежащими выше экваториальной плоскости, а левая–точками на, лежащими ниже этой плоскости.

Р и с. 1.10

Для линейно поляризованного света разность фаз равна нулю или целому, кратному . Тогда, согласно последнему уравнению соотношений , параметр СтоксаS₃равен нулю, так что линейная поляризация представляется точками на экваториальной плоскости.

Правая круговая поляризация представляется северным полюсом (E₁₀ = E₂₀ = E₀₀,S₁ = 0, = /2,S₂= 0,S₃=S₀), а левая поляризация–южным полюсом (E₁₀=E₂₀=E₀₀,S₁= 0,= –/2,S₂= 0,). Такое геометрическое представление различных состояний поляризации точками на сфере было предложено Пуанкаре. Оно чрезвычайно полезно в кристаллооптике для определения влияния материальных сред на состояние поляризации проходящего через них света. Сфераназывается сферой Пуанкаре.

В плоской монохроматической волне напряженность электрического поля (а также и магнитного поля) естьрегулярнаяфункциякоординативремени. Такая волна называется полностью поляризованной или просто поляризованной. Мы дали исчерпывающее представление о состояниях поляризации такой волны. Показали, что в общем случае такая волна поляризована эллиптически, а характеристики эллипса поляризации определяются амплитудами и фазами ортогональных компонент светового поляE_xиE_y.

Изложенное показывает, что электромагнитная волна с любой поляризацией может быть представлена в виде суперпозиции двух линейно поляризованных волн, плоскости колебаний электрического вектора (плоскости поляризации) которых взаимно перпендикулярны. Поэтому можно сказать, что электромагнитные волны обладают двумя независимыми состояниями поляризации.

Как мы видели, решением уравнений Максвелла служит монохроматическая волна, и поэтому она обязательно должна быть поляризована (в общем случае эллиптически). Однако опыт показывает, что излучение всех реальных источников света (кроме лазерных) неполяризовано. Это объясняется тем, что нам одновременно приходится наблюдать излучение огромного числа атомов, посылающих различно поляризованный свет. Кроме того, в каждом акте излученияатом испускает свет с новым состоянием поляризации. Таким образом, обычно наблюдается множество всех возможных ориентаций векторовии быстрая смена этих ориентаций, что и представляет собойестественныйсвет.

Естественныйсвет есть совокупность световых волн со всеми возможными направлениями колебаний, быстро и беспорядочно сменяющими друг друга; т.е. характеризуется неупорядоченностью направлений колебаний, совокупность эта статистически симметрична относительно волновой нормали.

Существует понятие частичнополяризованного света. Он характеризуется тем, что одно из направлений колебаний оказывается преимущественным, но не исключительным. Волновая нормаль уже не является прямой, по отношению к которой направления колебаний электрического (магнитного) вектора статистически равновероятны в плоскости, нормальной к этой прямой. Частично поляризованный свет можно рассматривать как смесь естественного и поляризованного. Можно в этом случае ввести понятие степени поляризации:

где и – средние значения квадратов двух взаимно перпендикулярных компонент напряженности электрического поля, выбранных в плоскости, перпендикулярной направлению распространения волны.

Если P = 0, то свет неполяризованный или естественный; еслиP = 100%, то поляризация света линейная.

На практике поляризованное излучение получают или от лазерных источников, механизм работы которых мы рассмотрим позже, или используют специальные приборы, называемые поляризаторами. Сих помощью можно не только поляризовать излучение, но ианализироватьсостояние поляризации.