Эллиптическая поляризация

В рассмотренном примере линейно поляризованной волны предполагалось, что вектор во всех точках направлен параллельно или антипараллельно осиx(см. рис. 1.7). В общем случае у плоской гармонической волны, распространяющейся вдоль осиz, отличны от нуля обе компонентыE_xиE_y, а вектор электрического поля имеет вид

,

где ,– единичные векторы, направленные вдоль осейОx,Oyдекартовой системы координат.

Рассмотрим волну, компоненты электрического поля которой изменяются по гармоническому закону

,

,

где сдвиг фаз между колебаниями.

Найдем уравнение траектории, по которой движется конец вектора в плоскостиz = const. Перепишем в виде

и с помощью исключим из этого равенства cos (t –kz) иsin (t –kz):

Напомним, что амплитуды E₁₀ иE₂₀предполагаются положительными числами. Перенесем первое слагаемое правой части на левую сторону, делим обе части наE₂₀и возводим их в квадрат.

.

Раскрываем скобки и приводим уравнение к виду

.

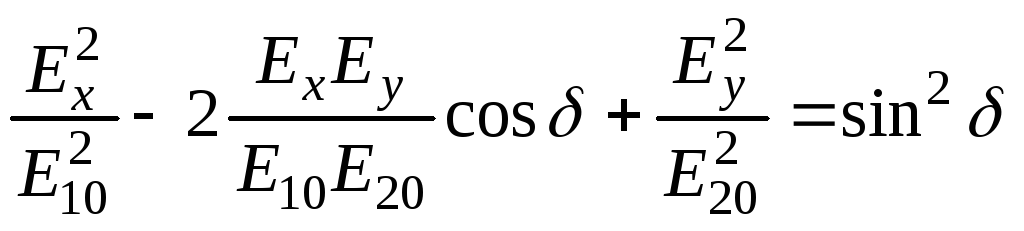Соотношение является уравнением конического сечения. Сечениеимеет форму эллипса, так как соответствующий детерминант неотрицателен, т. е.

.

Р и с. 1.8

Эллипс вписан в прямоугольник, стороны которого имеют длины 2E₁₀и 2E₁₀(рис. 1.8).Онкасается сторон прямоугольника в точкахAA (E₁₀,E₂₀cos) иBB (E₁₀cos,E₂₀).

Итак, в общем случае при распространении плоской монохроматической световой волны конец вектора в плоскостиz = constописывает эллипс. Аналогично ведет себя и вектор напряженности магнитного поля. Такая волна называетсяэллиптически поляризованной.

Представить себе электрическое поле такой волны при фиксированном tможно так: на поверхности прямого эллиптического цилиндра проведена винтовая линия, начала всех векторовнаходятся в точках оси цилиндра, концына винтовой линии, причем сам вектор везде перпендикулярен оси.

Правая и левая эллиптические поляризации

Двигаясь по эллипсу в плоскости z = const, конец вектораможет вращаться по часовой или против часовой стрелки. Для того чтобы различить эти два состояния, в оптике вводят понятияправойполяризации (для наблюдателя, смотрящего навстречу световому лучу, вращениепроисходит по часовой стрелке) илевойполяризации (вращение векторав противоположном направлении). Покажем, что направление вращения векторазависит от знака разности фаз. Выберем момент времениt₀, для которогоt₀–kz = 0. В этот момент, согласно формулам и ,

,

.

Так что .

Из формулы видно, что в тот момент, когда конец вектора достигает крайней правой точки своей траектории (рис. 1.8), имеемdE_y/dt < 0, если 0 <<, иdE_y/dt > 0, если – < < 0. Очевидно, что первый из этих случаев соответствует право поляризованной волне, а второй — лево поляризованной.

Итак, в общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса поляризации дается тремя параметрами E₁₀,E₂₀и. И, как видно из рис. 1.8, оси эллипса могут быть не параллельны осямOx и Oy. Однако если заданыE₁₀,E₂₀и разность фаз, относящиеся к произвольному положению осей, и если(0 <  /2) — угол, определяемый соотношением

,

то главные полуоси эллипса a и bи угол    , который большая ось образует с осьюOx, находятся из формул

,

где (    )–вспомогательный угол, определяющий форму и ориентацию эллипса колебаний, а именно:

.

Численное значение tgопределяет величину отношения осей эллипса, а знак прихарактеризует два варианта, которые можно использовать при описании эллипса. Из последней формулы видно, что при правой эллиптической поляризации, когдаsin > 0, то уголменяется в пределах 0 <  /4, что соответствует знаку "+" в формуле . Соответственно для левой поляризациизнак "–".

Параметры a,bиможно определить на опыте, а, зная эти величины, по формулам можно рассчитать амплитудыE₁₀,E₂₀и разность фаз.