Сферическая гармоническая волна

Если на сфере радиуса r₀задать гармоническое возмущение, синфазное во всех точках сферы

,

то возбуждаемая таким источником расходящаяся волна при r>r₀может быть представлена в виде:

Здесь в отличие от плоской волны амплитуда зависит от координаты, а фазовый и амплитудный фронты представляют собой сферы.

В комплексном представлении расходящаяся сферическая волна запишется так:

Наряду с плоской, сферическая гармоническая волна является эталонной волной, имеющей большое значение для оптики. Поэтому и сделан особый акцент на описание этих волновых процессов. Хотя сами по себе эти волны являются в значительной степени математической абстракцией, их роль в описании оптических явлений трудно переоценить. Во многих случаях реальный световой пучок можно разложить в спектр по плоским гармоническим волнам. Излучение реальной среды, состоящей из возбужденных атомов и молекул, часто можно представить как суперпозицию сферических волн.

Свойства плоской гармонической электромагнитной волны

Для анализа структуры плоской электромагнитной волны удобно записать уравнения Максвелла в символической форме с помощью векторного дифференциального оператора “набла”.

,

где – единичные векторы, направленные вдоль осейx,y,zдекартовой системы координат.

Принимая во внимание, что для произвольного векторного поля

уравнения Максвелла (1.1) – (1.4) можно записать так:

Будем искать решение этих уравнений в виде плоских гармонических волн

,

где и– постоянные векторы, не зависящие от времени, но компоненты которых могут быть комплексными. Подставляя выражения и в уравнение  –  и учитывая, что

получаем следующие соотношения:

,

,

.

Из соотношений и следует, что векторы иплоской волны перпендикулярны вектору, т.е. направлению распространения. Это означает, что электромагнитная волна являетсяпоперечной. Соотношения  –  показывают, что векторыивзаимно перпендикулярны. Таким образом, для плоской гармонической световой волны, распространяющейся в вакууме в произвольном направлении, векторы,иобразуют правую тройку взаимно перпендикулярных векторов (рис. 1.2).

Р и с. 1.2

Взяв от обеих частей  –  модули и учитывая взаимную ориентацию всех векторов, а также, что ,, ,находим следующие соотношения между значениями напряженности электрического и магнитного полей, а также между напряженностью электрического поля и магнитной индукцией плоской волны в вакууме:

,.

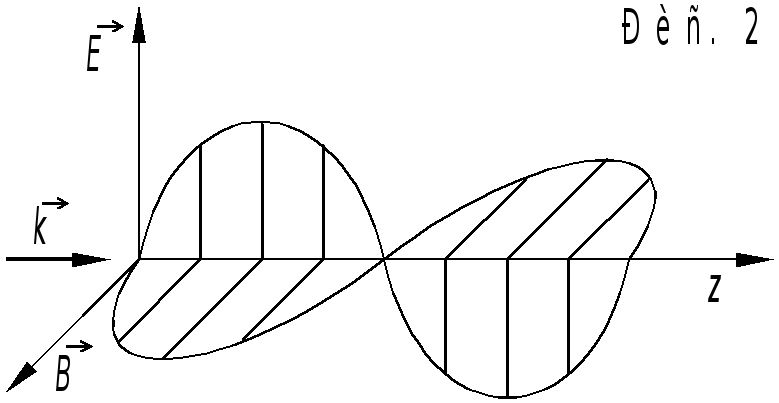
Нарис. 1.2 видно также, что в бегущей плоской волнеиизменяются в одинаковой фазе, т.е. одновременно достигают максимальных и нулевых значений.

Плотность потока энергии

Плотность потока энергии электромагнитного поля определяется вектором Умова - Пойнтинга

,

который указывает направление и количество энергии, переносимой световой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Модуль вектора в случае плоской волны может быть представлен в виде:

,

где учтено одно из соотношений .

Учитывая, что значение вектора электромагнитной волны оптического диапазона изменяется с частотами порядка 10¹⁵Гц, то следить за изменением этой величины во времени невозможно. Можно наблюдать и измерять лишь средние значения, как величиныЕ², так и величиныS, по очень большому числу периодов колебаний. Поэтому от мгновенных величин необходимо перейти к средним.

Учитывая, что для гармонических волн E=Е₀ cost, гдеЕ₀– амплитуда напряженности электрического поля волны, находим среднюю по времени плотность потока энергии, которую называют обычноинтенсивностьюсвета:

Обычно в эксперименте используют пучки света конечного сечения, по которому плотность потока распределена неравномерно. Чаще всего пучок имеет круговое сечение, распределение плотности энергии по которому аксиально симметричное и гауссово. Такой пучок называется гауссовым, и распределение средней плотности потока энергии имеет вид

где S₀– средняя плотность потока энергии в центре пучка (r= 0);r– расстояние от центра. На расстоянииr₀плотность потока энергии убывает ве= 2,72 раза. По обычной договоренности об обращении с экспоненциально убывающими величинами можно сказать, что радиус пучка равенr₀.

Гауссовы волны могут служить математической моделью излучения оптических квантовых генераторов (лазеров).