2. Волна де Бройля. Волновой пакет.

Де Бройль связал свободно движущуюся частицу, обладающую энергией и импульсом , с некоторой волной . Если движение частицы одномерно, то ей можно сопоставить некоторую плоскую волну. В соответствии с формулой Эйлера ( ) ее можно представить в комплексной форме:

- волна де Бройля,

где , а , поэтому уравнение волны де Бройля можно записать через параметры частицы:

,

где - фаза волны.

Условие , позволяет определить положение постоянной фазы волны. Дифференцируя это соотношение по времени, получим , т.е. - это скорость распространения одинаковой фазы волны, так называемая фазовая скорость .

Плоская волна бесконечна в пространстве, что плохо ассоциируется с пространственно локализованной частицей. Поэтому Э.Шредингер предположил, что частицу следует связывать не с плоской волной, а с пакетом волн (или группой волн). Волновой пакет – это суперпозиция волн, мало отличающихся друг от друга по и по направлению распространения. У волнового пакета амплитуда отличается от нуля лишь в небольшой области пространства (рис.8). Причем, чем уже спектр, охватывающий пакет, т.е., чем меньше , при которых , тем больше пространство, в котором пакет локализован, т.е. тем больше .

Пусть в группе волн изменяется пределах или соответственно изменяется в пределах , где

<< 1 ( << 1). Предположим также, что каждому значению соответствует волна с амплитудой . В малом интервале значений вблизи функцию в окрестности можно разложить в ряд Тейлора и ограничиться двумя первыми членами разложения

, где , ;

тогда результирующая волна, являющаяся суперпозицией волн, формирующих пакет, будет иметь вид:

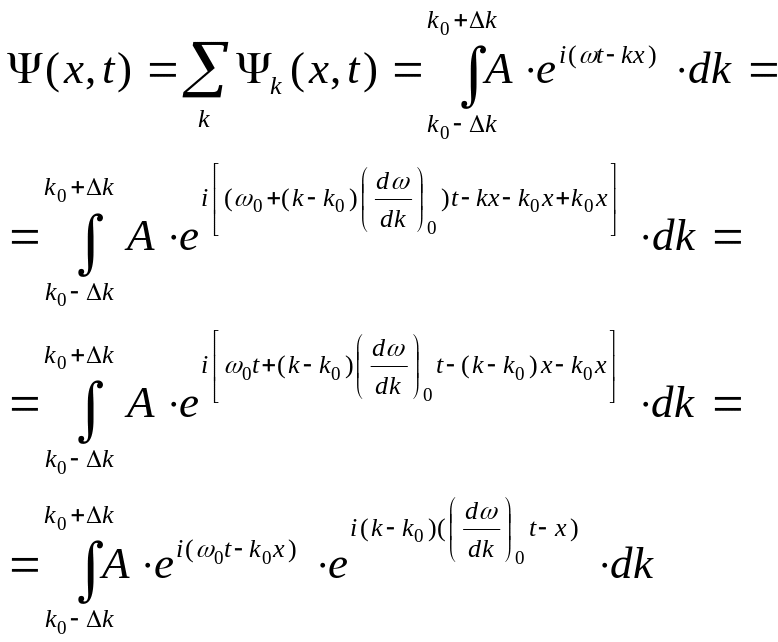
Произведем замену переменных: ,

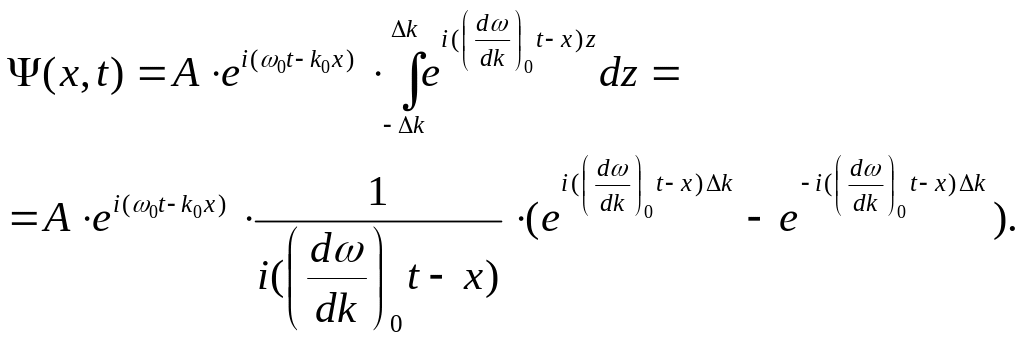
Из формул Эйлера

.

Тогда

.

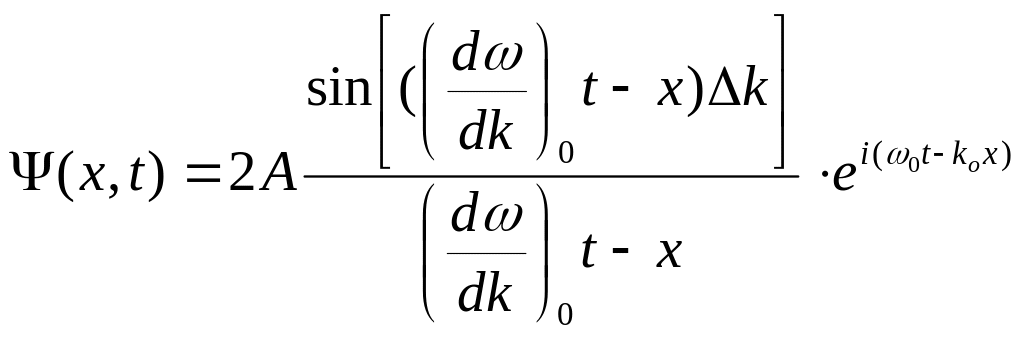Обозначив , получим

Это, по существу, волна с частотой и волновым числом , у которой модулирована амплитуда . Амплитуда пакета волн имеет максимум, когда

Следовательно координата максимума амплитуды, т.е. «центра тяжести», удовлетворяет соотношению . Отсюда скорость распространения «центра тяжести» пакета волн (а, следовательно, и энергии микрочастицы) будет определяться выражением

Величина называется групповой скоростью. (Сравним с фазовой скоростью ).

Учитывая, что полная энергия частицы определяется выражением , можно найти соответствующую ей групповую скорость:

Таким образом, групповая скорость равна скорости частицы.

Групповая скорость никогда не может превысить скорости света, тогда как фазовая скорость может быть больше скорости света, т.к. она не связана с переносом энергии.

2.4. Соотношение неопределенностей.

Волновой пакет имеет определенную пространственную протяженность. Оценим ее. В момент времени сделаем «мгновенную фотографию» пакета. Амплитуда пакета будет равна нулю в том случае, когда ( при ). Но при . Отсюда или , более точно . Это соотношение неопределенностей Гейзенберга.

Из соотношения неопределенностей следует, что, чем точнее задано значение импульса ( ), тем менее точно определена координата микрочастицы ( ) и наоборот. Как понимать это соотношение? Дело в том, что величины и - это характеристики частицы (макрообъекта). Микрочастица в силу своего корпускулярно-волнового дуализма не может быть строго описана характеристиками макрочастицы, - отсюда такая неопределенность значений и .

Рассматривая различные способы измерения положения и импульса частицы, Гейзенберг пришел к выводу о том, что условия, благоприятные для точного измерения координаты частицы (малая длина волны), неблагоприятны для точного измерения ее импульса (большая отдача при столкновении с фотоном), и наоборот.

Соотношение неопределенностей указывает, в какой мере можно пользоваться понятиями классической механики применительно к микрочастицам. Это соотношение является одним из фундаментальных положений квантовой механики.

Анализ выражения для волнового пакета позволяет получить еще одно важное соотношение. Оценим время , за которое волновой пакет переместится на (т.е. на половину своей ширины). Это соответствует значению (как было установлено ранее). Но в данном случае это соответствует условию , из которого следует, что . Это соотношение следует понимать следующим образом: чем меньше временная длительность волнового пакета , тем больший частотный интервал он охватывает. Умножив на , получим , точнее, - это то же соотношение неопределенностей для энергии и времени. Как его понимать? Чем дольше частица находится в данном состоянии ( ), тем меньше неопределенность ее энергии ( ).

Из соотношения неопределенностей Гейзенберга вытекает важное следствие:

.

Рассмотрим частицу с большей массой, приближающейся к величине, характерной для макрообъекта. Неопределенность координаты и скорости такой частицы будет меньше. Это соответствует случаю классической механики. Классическая механика – это предельный случай механики микрочастиц (квантовой механики) для массивных объектов. Значит, выражения, описывающие те или иные закономерности микрообъектов в пределе (при переходе к массивным объектам), должны переходить в обычные, классические выражения. В этом заключается одно из проявлений принципа соответствия, сформулированного Нильсом Бором в 1923 г.: «Всякая новая теория в физике должна сводиться к хорошо установленной классической теории, если эта теория прилагается к специальным случаям, которые успешно описываются менее общей теорией».