Решение

Общий (агрегатный) индекс цен:

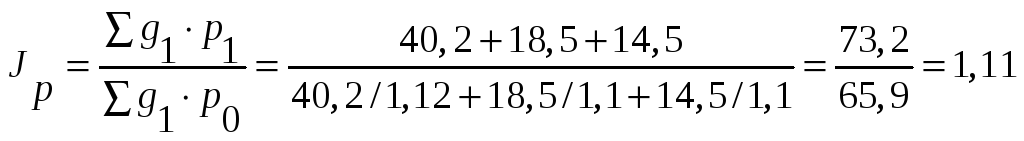
где - цена в первом квартале

- цена во втором квартале

- объем продукции во втором квартале

- товарооборот в соответствующем квартале

Общий (агрегатный) индекс товарооборота (в фактических ценах):

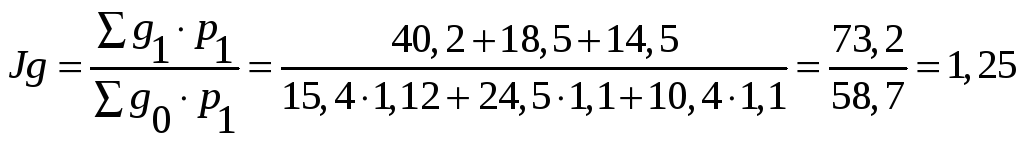
где - объем продукции в первом квартале

- объем продукции во втором квартале

- цена во втором квартале

- товарооборот в соответствующем квартале

Общий (агрегатный) индекс товарооборота (при неизменных ценах):

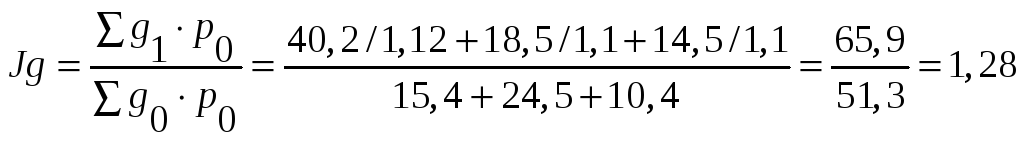
где - объем продукции в первом квартале

- объем продукции во втором квартале

- неизменная цена (равна цене в первом квартале)

- товарооборот в соответствующем квартале

Изменение расходов населения в результате изменения цен:

(Млрд.Руб.)

где - изменение цен во II квартале по сравнению с I кварталом

- товарооборот в соответствующем квартале

Ответ

Общий (агрегатный) индекс цен = 1,11

Общий (агрегатный) индекс товарооборота в фактических ценах = 1,25

Общий (агрегатный) индекс товарооборота при неизменных ценах = 1,28

Изменение расходов населения в результате изменения цен = 8,1 (млрд.р.)

ЗАДАЧА 7

За базисный и отчетный периоды на предприятии выработано продукции соответственно на 20 и 22 млрд. р. (в действующих ценах). В отчетном периоде цены на продукцию были повышены в среднем на 15%.

Определить:

а) изменение физического объема продукции;

б) изменение стоимости продукции (в абсолютном выражении) за счет изменения

физического объема продукции и изменения цены.

Решение

- товарооборот в базисном периоде (по условию)

- товарооборот в отчетном периоде (по условию)

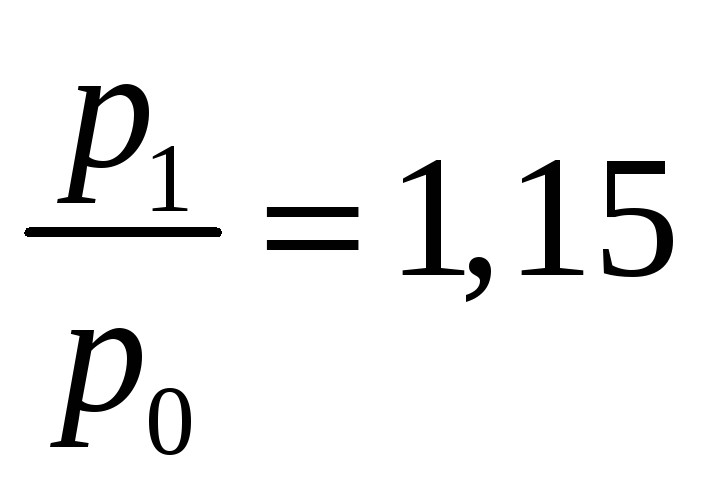- отношение цен в отчетном и базисном периодах (по условию)

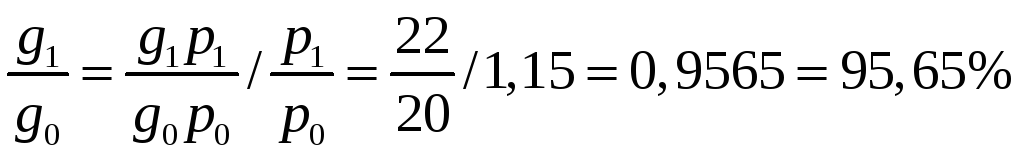- изменение объема продукции

Изменение стоимости продукции за счет изменения физического объема продукции:

Изменение стоимости продукции за счет изменения цены продукции:

Ответ

Изменение объема продукции = уменьшение на 4,35 %

Изменение стоимости продукции за счет изменения объема = уменьшение на 0,88 млрд.р

Изменение стоимости продукции за счет изменения цены = увеличение на 2,88 млрд.р.

ЗАДАЧА 8

Изобразите данные задачи 5 с помощью круговых графиков и ломаной кривой.

Какой из этих графиков наиболее наглядно изображает изменение количества телефонных аппаратов за 6 лет?

Сформулируйте выводы, следующие из графических изображений.

Решение

Исходные данные:

Год	1-й	2-й	3-й	4-й	5-й	6-й
Телефоны, тыс.шт.	94,5	98,2	110,0	130,2	144,8	162,5

В круговых графиках извлекаются квадратные корни из сравниваемых статистических величин, предварительно разделенных на π. Устанавливается масштаб и строится круг с радиусом, пропорциональным вычисленной величине. Таким образом:

Расчитаем соответствующие радиусы и построим круговой график по данным радиусам:

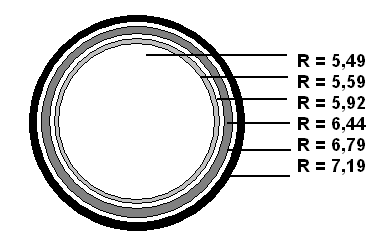
Аналогичный график в виде ломаной кривой имеет вид:

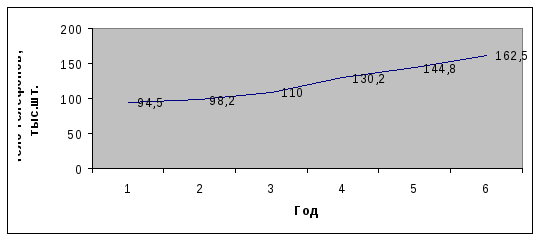
Вывод: график в виде ломаной кривой более наглядный, в частности из-за того, что полученные радиусы при построении кругового графика совсем незначительно отличаются друг от друга (из-за квадратичной зависимости площади круга от радиуса)

ЗАДАЧА 9

Контрольная проверка комплектующих изделий дала следующие результаты:

Вес упаковки, Wi, г	48–49	49–50	50–51	51–52
Количество упаковок, ni, шт.	20	50	20	10

С вероятностью 0,954 определите:

а) средний вес упаковки в выборке; б) предельную ошибку среднего веса упаковки;

в) границы генеральной средней (при условии, что выборка составляет 25% от

генеральной совокупности).

Решение

Объем выборки: ,

где m - общее число значений в ряду

n_i - количество упаковок в i-той группе

Средний вес упаковки в выборке: ,

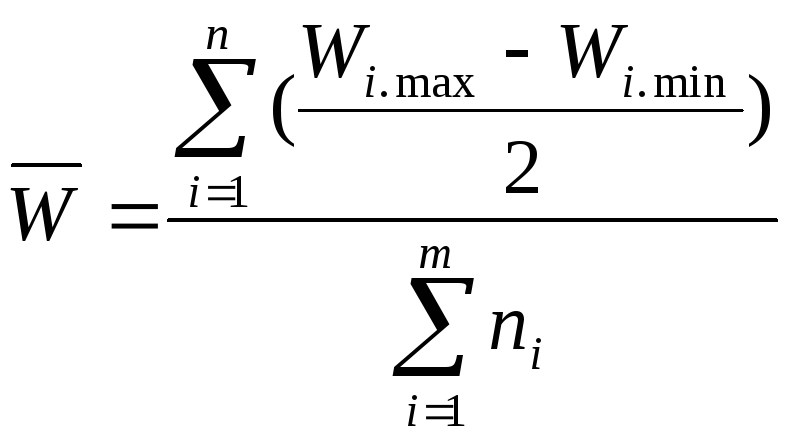где n_i - вес упаковки в i-той группе

- нижняя граница соответствующего интервала

- верхняя граница соответствующего интервала

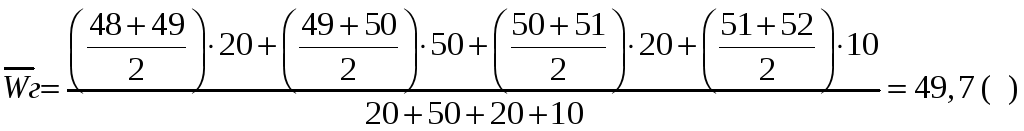
Находим выборочную дисперсию веса упаковки:

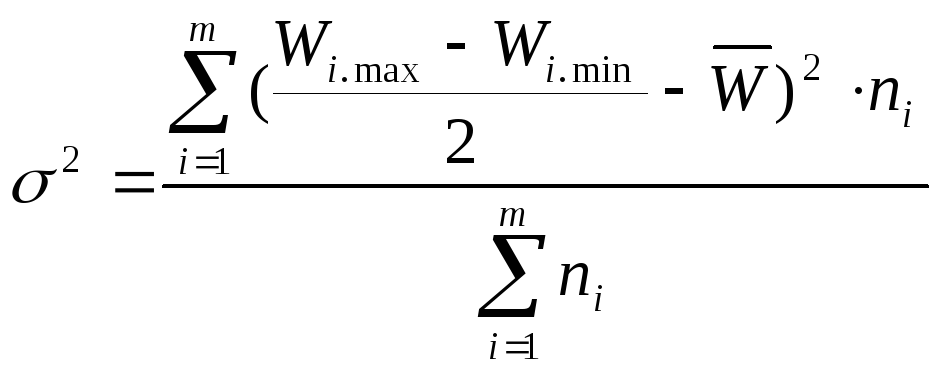
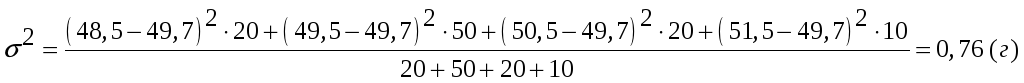
Зависимость между в генеральной и выборочной дисперсиями:

.

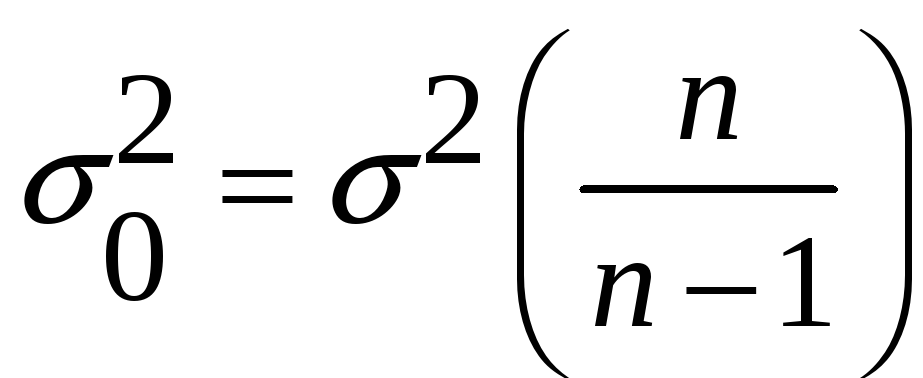Поскольку , тип отбора – бесповторный, а выборка составляет 25% от генеральной совокупности (по условию), то среднюю ошибку выборки находим по формуле:

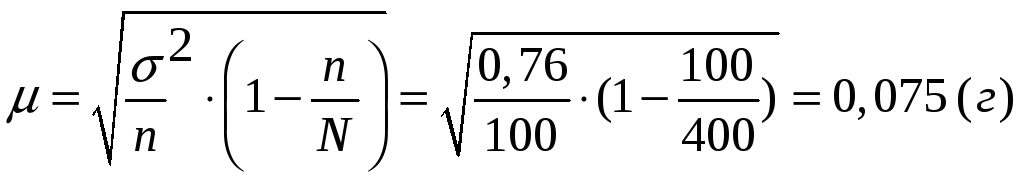, где N – объем генеральной совокупности

Вероятность, заданная в условии (0,954), соответствует кратности ошибки t = 2 (т.е. в 95 случаях из 100 характеристика генеральной совокупности будет совпадать с соответствующей характеристикой выборки).

Находим предельную ошибку среднего веса упаковки:

Границы генеральной средней (среднего веса упаковки для всей партии):

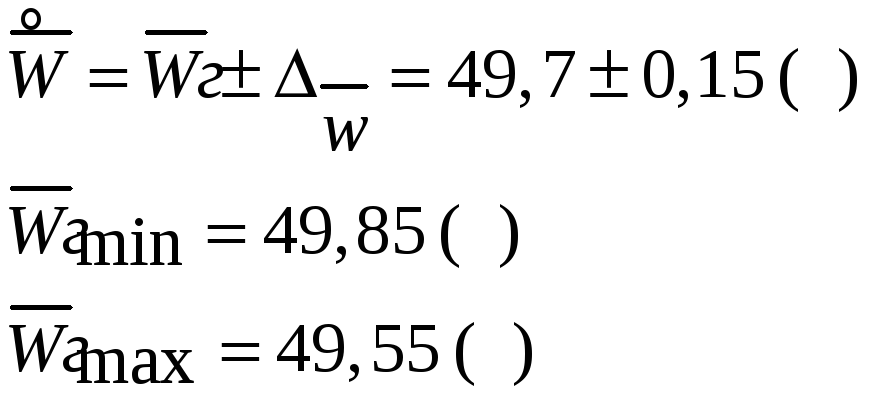
где - минимальное значение генеральной средней

- максимальное значение генеральной средней

Ответ

Средний вес упаковки в выборке = 49,7 г.

Предельная ошибка среднего веса упаковки = 0,15 г.

Границы генеральной средней = (49,55 .. 49,85) г.

ЗАДАЧА 10

Имеются следующие данные о длительности производственного стажа и общей сумме дневной заработной платы рабочих цеха:

Группа рабочих по стажу работы, лет	Число рабочих в группе	Общая сумма дневной зарплаты по группе, тыс. р.
1–3	3	270
4–6	3	350
7–9	3	450
10 и более	3	600

Определите:

а) среднюю дневную заработную плату рабочего в каждой группе и в целом по цеху;

б) вид корреляционной зависимости между дневной заработной платой и длительностью

производственного стажа рабочих;

в) параметры уравнения регрессии;

г) тесноту зависимости.