
Критерий Сильвестра
f(x1, x2, …, x4) = a11x1² + a21x1x2 + a21x2x1 + … + a1nx1xn + an1xnx1 + a22x2² + … + annxn² – квадратичная форма.
Матрица квадратичной формы:
 a11
a12
… a1n
a11
a12
… a1n
Anxn = a21 a22 … a2n
. . . . . . .
an1 an2 … ann
 a11
a12
a13
a11
a12
a13
∆ 1
=
an,
∆2
=
a11
a12
, ∆3
= a21
a22
a23
, …, ∆n
= detA
1
=
an,
∆2
=
a11
a12
, ∆3
= a21
a22
a23
, …, ∆n
= detA
a21 a22 a31 a32 a33
∆1, ∆2, …, ∆n – угловые миноры матрицы А
Критерий Сильвестра заключается в следующем:
1) Квадратичная форма положительна определена <=> ∆1>0, ∆2>0, …, ∆n>0
(все угловые миноры строго положительны)
2) Квадратичная форма отрицательно определена <=> ∆1<0, ∆2>0, ∆3<0, …, (-1)ⁿ∆n>0
(чередования знаков: -, +, -, +, …)
3) Квадратичная форма квазиположительна <=> миноры k-го порядка
∆(i1, i2, …, ik) ≥ 0 [i1 < i2 < … < ik, k = (1,n)]
4) Квадратичная форма квазиотрицательна <=> (-1)ⁿ∆(i1, i2, …, ik) > 0
(∆(i1, i2, …, ik) – миноры k-го порядка)
5) В остальных случаях квадратичная форма будет знакопеременной.
Пример 1
Определить знак квадратичной формы:
f = -x1² - 5x2² - 6x3² + 4x1x2 – 2x1x3
Составим матрицу квадратичной формы:

-1 2 -1
A = 2 -5 0
-1 0 -6
-1 2 -1
∆ 1 = -1 = -1; ∆2 = -1 2 =1; ∆3 = 2 -5 0 = -30 + 5 + 24 = -1
2 -5 -1 0 -6
∆1 < 0, ∆2 > 0, ∆3 <0
По критерию Сильвестра f < 0 (отрицательно определена)
Пример 2
При каком значении параметра µ следующая квадратичная форма будет положительно определена.
F = 5x1² + x2² + μx3² + 4x1x2 – 2x1x3 – 2x2x3
F>0, μ=?
М атрица
квадратичной формы:
атрица
квадратичной формы:
5 2 -1
A3x3 = 2 1 -1
-1 -1 μ
Критерий Сильвестра:
∆1=5
∆ 2=
5 2 = 5-4=1
2=
5 2 = 5-4=1
2 1
∆1>0, ∆2>0


 5
2 -1 -1 5
2 -1 3 2 -1
5
2 -1 -1 5
2 -1 3 2 -1
∆3= 2 1 -1 > 0 -3 -1 0 > 0 -2 -1 0 > 0
- 1
-1 μ
-1 -1 μ
0 -1 μ
1
-1 μ
-1 -1 μ
0 -1 μ
־¹
(раскладываем по третьей строке)
- 1
· (-1) 5 ·
3 -1 + μ
(-1) 6
· 3 2 > 0
1
· (-1) 5 ·
3 -1 + μ
(-1) 6
· 3 2 > 0
-2 0 -2 -1
-2 + μ > 0
Ответ: при μ > 2, F > 0
§3 Приведение квадратичной формы к каноническому виду.
С помощью линейных преобразований квадратичную форму
F = F (x1, x2, …, xn) можно привести к каноническому виду
F = b1y1² + b2y2² + … + bnyn2
Полезная информация:


a11 a22 … a1n x1
Пусть дана матрица Anxn = a21 a22 … a2n Xnx1 = x2
………. …
an1 an2 … ann xn
Рассмотрим произведение:
Anxn · X nx1 = Y nx1

y1
Y = y2
…
yn
Предположим, что yi = λ · xi, i = (1,n), λЄR, λ ≠ 0
Тогда имеем равенство:
(*) A · X = λ · X
В этом случае вектор-столбец X называется собственным вектором матрицы А.
Коэффициент пропорциональности λ называется характеристическим числом матрицы A или собственным значением.
Как найти характеристическое числа и собственные вектора?
![]()
![]() -
это однородная система линейных уравнений
-
это однородная система линейных уравнений

Система
![]() по теореме Крамера имеет ненулевые
решения
по теореме Крамера имеет ненулевые
решения ![]()
![]()
Таким образом, для нахождения характеристических чисел необходимо и достаточно решать характеристическое уравнения.

Пусть
![]() характеристическое
число
характеристическое
число
Для нахождения
собственного вектора, соответствующего
числу ![]() подставлляем
подставлляем
![]() в систему
в систему ![]()
Т.к. ранг матрицы
![]()
![]()
То система имеет бесконечно много решений.
Можно доказать,
что если ![]() характеристические числа матрицы
квадратичной формы f,
то каноническая
форма имеет вид:
характеристические числа матрицы
квадратичной формы f,
то каноническая
форма имеет вид:
f
=![]() +…+
+…+![]()
Рассмотрим решение задачи (аналогичной той, которая есть в домашней контрольной работе)
Задача
Определить вид кривой.
Построить линию
![]()
Решение
Обозначим ![]()
Это квадратичная формула от двух переменных
![]() ,
, ![]() ;
; ![]()
![]() (матричная
запись f
в системе
координат
(матричная
запись f
в системе
координат![]() )
)
Будем искать другую
систему координат ![]() ,
в которой f
имеет
каноническую форму.
,
в которой f
имеет
каноническую форму.
ШАГ 1: Составляем характеристическое уравнение
![]()
![]()
![]()
Характеристические
числа
Шаг 2. Находим собственные векторы для каждого числа.
Пусть
λ1 = 20
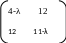


 .
.


 -16x
+ 12y = 0
-16x
+ 12y = 0
.



12x – 9y = 0
[Т.к. r(A)=1, то достаточно оставить одно уравнение.]
1 2x
– 9y = 0 => x=3/4y,
2x
– 9y = 0 => x=3/4y,
![]() y
y![]() R
R
С
 обственный
вектор в общем виде:
обственный
вектор в общем виде:

Пусть y=4 b1 =

В дальнейшем нам понадобится орт b1.
дальнейшем нам понадобится орт b1.
|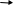


 |b1||
=
|b1||
=
![]() =
5 b1
= e1
=
=
5 b1
= e1
=
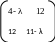
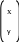


П
 усть
λ2 = –5
усть
λ2 = –5
9x + 12y = 0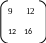







12x + 16y = 0

Т.к.
r(A)=1 =>
9x + 12y=0 =>
x= –4/3y,
![]() y
R
y
R

С
 обственный
вектор в общем виде:
обственный
вектор в общем виде:
П усть
y=3 b2
=
усть
y=3 b2
=


||b2|| = 5
О

 рт
этого вектора b2 =
e2
=
рт
этого вектора b2 =
e2
=
З аметим, что e1, e2 образуют ортонормированный базис.
К
онтроль!
||e1||
= ||e2||
= 1 (e1
![]() e2)
e2)
e 1
e2
= 0 3/5 (–4/5) + (4/5) (3/5) = 0
1
e2
= 0 3/5 (–4/5) + (4/5) (3/5) = 0
 Шаг
3.
Составляем ортонормированную матрицу
Q
= (e1,
e2).
Шаг
3.
Составляем ортонормированную матрицу
Q
= (e1,
e2).
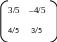
Q =
e1 e2
Шаг 4. Переход к новой системе координат.


T
= Q
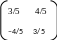

 =
=
 x1
= 3/5x + 4/5y
x1
= 3/5x + 4/5y
x2 = –4/5x + 3/5y
Шаг 5. В новой системе координат.
S (x1,
y1) = λ1x12
+ λ2y1 2
(x1,
y1) = λ1x12
+ λ2y1 2
S
 (x1,
y1) = 20x12
+ 5y12
(x1,
y1) = 20x12
+ 5y12
Каноническая форма.
Шаг 6
В новой системе координат X1OY1 уравнение нишей линии имеет вид
20x12 + 5y1 2= - 20 | : 20
![]()
сопряженная гипербола
a=1
b=2

Алгебраические поверхности второго порядка.
Алгебраической поверхностью второго порядка называется поверхность S, уравнение которой в декартовой прямоугольной системе координат имеет вид :
Ax2+By2+Cz2+2Exz+2Fyz+Gx+Hy+Iz+K=0
(A2+B2+C2≠0)
Если поверхность невырожденная (т.е. уравнение не задает Ø), то преобразование декартовой прямоугольной системы координат, это уравнение может быть приведено к одному из указанных видов, называемых каноническими и определяющими тип поверхности.
Эллипсоид
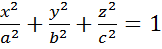
Гиперболоид
Однополостный
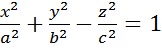
Двухполостный

Параболоид
Двухполостной параболоид
Гиперболический параболоид
 (p>0,
q>0)
(p>0,
q>0)
Эллиптический параболоид
 (p>0,
q>0)
(p>0,
q>0)Конус второго порядка

Цилиндр второго порядка
Эллиптический
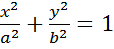
Гиперболический
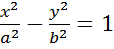
Параболический
 , p>0
, p>0
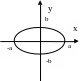
Э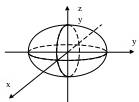 ллипсоид
ллипсоид
![]()
Сечения плоскостями
y
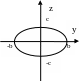 =0
=0
![]()
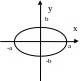 x=0
x=0
![]()
z=0
![]()

Сфера
![]()

Однополостный гиперболоид
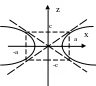
![]()
Сечение плоскостями
y =0
=0
![]()
 x=0
x=0
![]()
z=0
Двухполостный гиперболоид
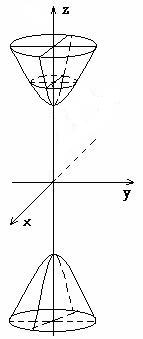
![]()
Сечения плоскостями:
z=0
![]() (нет)
(нет)
о.д.з. ![]() =>
=> ![]()
|
z
| z|
> c
z|
> c
|
a
c
x![]() → эллипс
→ эллипс
-a
y
-c
z![]() сопряженная гипербола
сопряженная гипербола

x=0
![]()
Г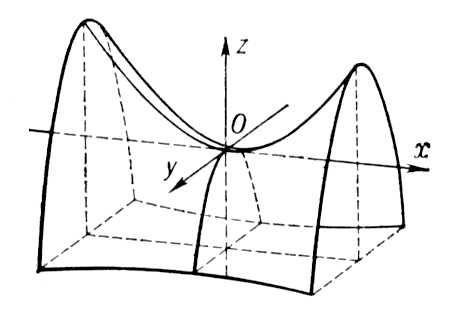 иперболический
параболоид
иперболический
параболоид

![]() (p>0,
q>0)
(p>0,
q>0)
С ечения
на плоскости
ечения
на плоскости
z=0
![]()
![]()
при z
> 0 ![]()
![]()
z
= 1 ![]() гипербола
гипербола
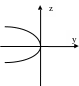 z
= -1
z
= -1 ![]() сопряженная
гипербола
сопряженная
гипербола
x=0
![]()
![]()
 y=0
y=0
![]()
![]()
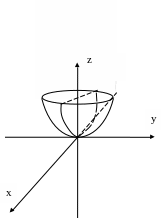
Э ллиптический
параболоид
ллиптический
параболоид
z
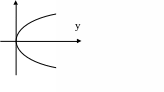
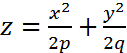 (P>0,
q>0)
(P>0,
q>0)
Сечения:
X=0
![]()
z
x

Y=0
![]()
Z=0 (0,0,0) – вершина
z≥0
z=z0
![]() - эллипс
- эллипс
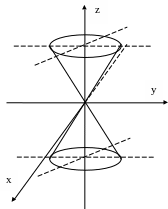
Конус второго порядка
![]()
z=c ![]() (эллипс)
(эллипс)
z=-c
x=0
![]()
y=0
![]()
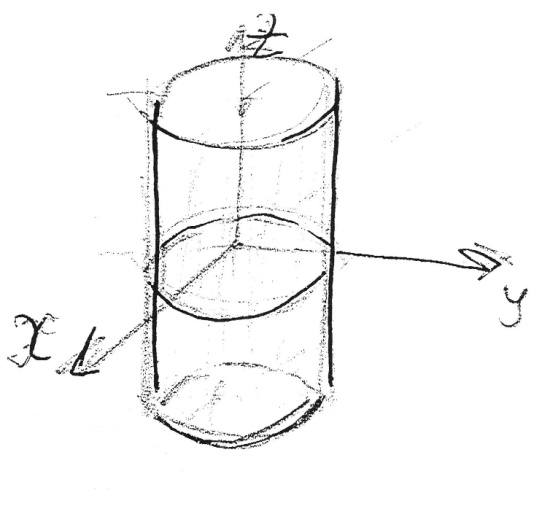 Эллиптический
цилиндр
Эллиптический
цилиндр
![]()
 Гиперболический
цилиндр
Гиперболический
цилиндр
![]()

Параболический
цилиндр
![]() ,
,
![]()
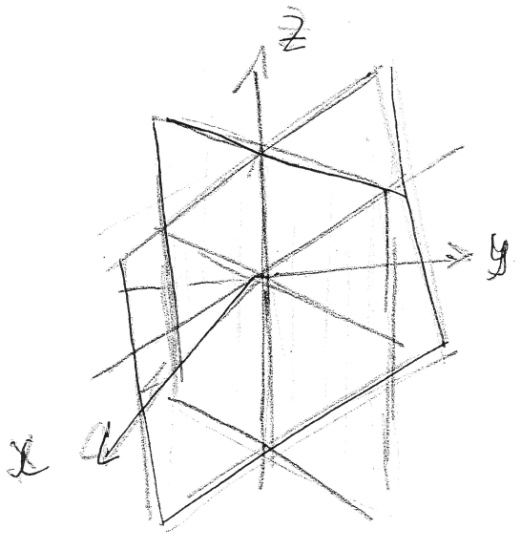 Пара
пересекающихся плоскостей
Пара
пересекающихся плоскостей
![]()
![]()
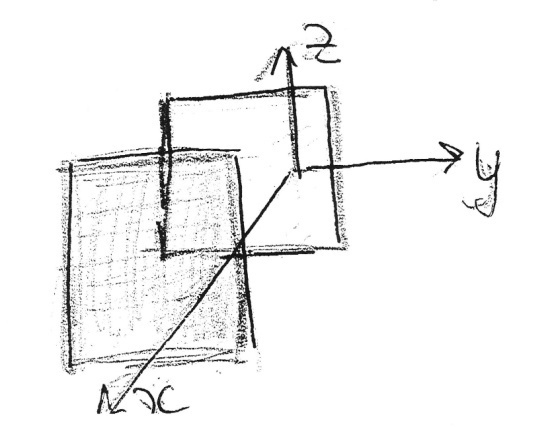
Пара параллельных плоскостей
![]()
![]()
Цилиндрические поверхности
Пусть (l) некоторая кривая, лежащая на поверхности S.
Зададим некоторою прямую U (Будем называть «Ось»)

Чтобы получилась цилиндрическая поверхность будем проводить множество прямых q ll u так, чтобы они пересекали нашу кривую (l) В дальнейшем будем называть кривую направляющей, а прямую q – образующей цилиндрическую поверхность. Чтобы узнать, является ли данная поверхность цилиндрической в системе координат (х О у) посмотрите внимательно на уравнение, которым задаём данную поверхность. Если в уравнении отсутствует какая-либо координата, то это уравнение задает цилиндрическую поверхность с образующей, параллельной ‘отсутствующей’ координатной оси, т.е. такими
у равнениями
могут быть: 1) F
(x,y)
= 0 (q
ll
Oz)
равнениями
могут быть: 1) F
(x,y)
= 0 (q
ll
Oz)
2) F (x,z) = 0 (q ll Oy)
3) F (y,z) = 0 (q ll Ox)
Рассмотрим примеры:
1) y = x2 В плоскости z = 0 (xOy)
Строим параболу и проводим
множество прямых q ll Oz

2) x2 + y2 = 4
В плоскости у = 0 ( хОz) строим окружность с центром (0,0) и R = 2 и проводим множество прямых ll Оу
Конические поверхности
Пусть точка О нам известна. Будем называть ее вершиной конической поверхности l – произвольная кривая линия на поверхности S.
Если проводить множество прямых q, проходящих через вершину О и пересекающих данную кривую l, то мы получим коническую поверхность. Кривую l называем направляющей, а прямую q – образующей.

В декартовой системе координат уравнение конической поверхности имеет вид:
F (x, y, z) = 0, но функция F обладает свойствами ‘однородность’ степени ‘k’.
F (tx, ty, tz) = tk F( x,y,z), t € R, k =1,2,3…
Например: 2х3-4y3+z3=0
конус третьего порядка О (0, 0, 0 )
 All
rights
reserved
©
All
rights
reserved
© 
