Г осударственный Университет

Высшая Школа Экономики

в Санкт-Петербурге

Анисимова Н.П.

Методический материал по теме:

Квадратичные формы

Санкт-Петербург

2009

Методический материал по теме: Квадратичные формы.

§1. Определение квадратичной формы.

Рассмотрим следующие функции:

Обозначим А_{1 1}=(а_{1 1}) – матрица коэффициентов

1. f(x₁) = a₁₁x₁²

2. f(x₁x₂) = a₁₁x₁² + a₁₂x₁x₂ + a₂₁x₂x₁ + a₂₂x₂² = a₁₁x₁² + 2a₁₂x₁x₂ + a₂₂x₂²

(если а₁₂=а₂₁)

Матрица коэффициентов:

А_2x2= а₁₁ а₁₂ симметричная матрица

а₂₁ а₂₂ относительно главной диагонали

Заметим, что А_2x2 = А^т_2x2

3. f(x₁,x₂,x₃) = a₁₁x₁² + a₁₂x₁x₂ + a₂₁x₂x₁ + a₁₃x₁x₃ + a₃₁x₃x₁ + a₂₃x₂x₃ + a₃₂x₃x₂ + a₂₂x₂² + a₃₃x₃² = a₁₁x₁² + a₂₂x₂² + a₃₃x₃² + 2(a₁₂x₁x₂+a₁₃x₁x₃+a₂₃x₂x₃)

Если а₁₂=а₂₁, а₁₃=а₃₁, а₂₃=а₃₂.

М атрица коэффициентов:

А_3x3 = а₁₁ а₁₂ а₁₃ Матрица, симметричная

а₂₁ а₂₂ а₂₃ относительно главной диагонали

а₃₁ а₃₂ а₃₃

А_3x3 = А^т_3x3

Например,

1. f(x₁,x₂) = 2x₁² + 3x₁x₂ – 4x₂²

A_2x2 = 2 1,5

1,5 -4

2) A_3x3 = -1 0,5 -0,6

0,5 4 0,3

-0,6 0,3 -8

f(x₁,x₂,x₃) = -x₁² + 4x₂² – 8x₃² +2*0,5 x₁x₂ – 2*0,6x₁x₃ + 2*0,3x₂x₃

В рассмотренных примерах мы имеем дело с функцией, которая в общем виде зависит от «n» переменных и задается определенной формулой, которой соответствует матрица коэффициентов.

Определение.

Квадратичной формой от «n» переменных называется функция вида:

_{n n}

f(x₁,x₂,x₃,…,xn) = Σ Σ a_ij x_i x_j

^{j=1 i=1}

Матрица коэффициентов – это симметричная матрица^.

A _nxn = a₁₁ a₁₂ … a_1j … a_1n

a₂₁ a₂₂ … a_2j … a_2n a_ij = a_ji

-------------------------- (i≠5)

a_i1 a_i2 … a_ij … a_in

--------------------------

a_n1 a_n2 … a_nj … a_nn

A_nxn = A^т_nxn

Если det A≠0, то квадратичная форма невырожденная.

Если ввести матрицу:

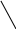
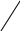X₁

= X₂

X₃ ,то квадратичную форму можно записать в матричной форме:

(2) f(x₁,x₂,x₃)=X^T_1xn×A_nxn×X_nx1

§2 Классификация квадратичных форм. Критерий Сильвестра.

Опр.1 Будем говорить, что квадратичная форма f =f(x₁,x₂,…x_n) положительно определена, если для (x₁,x₂,…x_n) f (x₁,x₂,…x_n)› 0 (кроме x₁=x₂…=x_n=0)

Опр.2 Будем говорить, что квадратичная форма f =f(x₁,x₂,…x_n) отрицательно определена, если для (x₁,x₂,…x_n) f (x₁,x₂,…x_n)‹ 0 (кроме x₁=x₂…=x_n=0)

Опр.3 Квадратичная форма называется квазиположительной, если f(x₁,x₂,…x_n)≥0, но неверно f (x₁,x₂,…x_n)› 0

Опр.4 Квадратичная форма f (x₁,x₂,…x_n) квазиотрицательна, если f≤0, но неверно f‹0

Замечание

Если говорят, что квадратичная форма неотрицательна, то это возможно одно из двух: или S положительная или квазиположительная, т.е. f≥0

Если говорят, что квадратичная форма неположительна, то это возможно: нулевая, отрицательная или квазиотрицательная

Если форма не удовлетворяет условиям перечисленным выше, то это знакопеременная форма.

Рассмотрим примеры

1. f(x)=ax² (x≠0)

Если а›0, то f›0 (положительно определенная)

Если a‹0, то f‹0 (отрицательно определенная)

2. f(x₁,x₂)=x₁²-6x₁x₂+9x₂²

f(x₁,x₂)=(x₁-3x₂)² f≥0 (неотрицательна)

3. f(x₁,x₂,x₃)=-9x₁²-x₂²-3x₃² f‹0 (x₁,x₂,x₃≠0)

4. f(x₁,x₂,x₃)=-(x₁+x₂-4x₃)²-9 f‹0

x₁,x₂,x₃ отрицательно определена

В общем случае трудно установить знак квадратичной формы.