СМиФ

Вариант 19

1.а. (𝑝 | 𝑞) | (𝑝 | 𝑞) ≡ 𝑝 ∧ 𝑞.

(𝑝 | 𝑞) = (~p) ∨ (~q)

p	q	𝑝 | 𝑞	(𝑝 | 𝑞) | (𝑝 | 𝑞)
0	0	1	0
0	1	1	0
1	0	1	0
1	1	0	1

p		q		𝑝 ∧ 𝑞
0	0		0
0	1		0
1	0		0
1	1		1

1.б. А = {1, 2, 3}

а) R₁ = {(2, 2), (1, 1), (3, 3)}

Отношение является отношением эквивалентности, если выполняются следующие условия:

- R₁ – рефлексивно, т.е. ∀а А (a ~ a) – выполняется

- R₁ – симметрично, т.е. ∀a, b A (a ~ b) → (b ~ a) – выполняется

- R₁ – транзитивно, т.е. ∀a, b, c A (a ~ b) ^ (b ~ c) → (a ~ c) – выполняется

Значит отношение R₁ является отношением эквивалентности на А.

б) R₂ = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (3, 2), (2, 1)}

Отношение является отношением эквивалентности, если выполняются следующие условия:

- R₁ – рефлексивно, т.е. ∀а А (a ~ a) – выполняется

- R₁ – симметрично, т.е. ∀a, b A (a ~ b) → (b ~ a) – не выполняется, т.к. (3 ~ 2) → (2 ~ 3)

Значит отношение R₂ не является отношением эквивалентности на А.

2.а. v = {a, b, c}; E = {(a, b), (b, c), (c, b), (c, a)}

outdeg (a) = 1, outdeg (b) = 1, outdeg (c) = 2

indeg (a) = 1, indeg (b) = 2, indeg (c) = 1

Вершина называется источником, если indeg (v) = 0. Для данного графа вершина источник отсутствует.

Вершина называется стоком, если outdeg (v) = 0. Для данного графа вершина сток отсутствует.

2.б.

a)

б) пути длиной 2: v₁v₂v₃, v₁v₂v₄.

3. 𝐴 = , 𝐵 =

U = ∨ =

𝐼 = ∧ =

= =

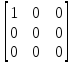
4.

1) a = 2n, n = 0, ±1, ±2, … , a ∈ G.

b = 2k, k = 0, ±1, ±2, … , b ∈ G.

c = a + b = 2n + 2k = 2(n+k)=2m, m = 0, ±1, ±2, … ⇒ c ∈ G.

2) a+(b+c) = (a+b)+c.

2n+(2k+2m)=2n+2(k+m)=2(n+k+m);

(2n+2k)+2m=2(n+k)+2m=2(n+k+m);

3) e = 0;

e + a = a + e = a,

0 + a = a + 0 = a.

4) a + ~a = ~a + a = e,

~a = -a;

a + (-a) = (-a) + a = 0.

5. (𝑥 + 1)())= )=

=1))=

6.a.

. k = 3, r = 2, n = 5 (k – кол-во информационных символов, r – кол-во

проверочных символов, n – длина кодового слова

- проверочная матрица.

6.б. Таблица смежных классов:

00000	00101	01011	01110	10011	10110	11000	11101
10000	10101	11011	11110	00011	00110	01000	01101
00100	00001	01111	01010	10111	10010	11100	11001
00010	00111	01001	01100	10001	10100	11010	11111

7.а. Получено слово . В таблице смежных классов оно расположено в самой верхней строке. Это означает, что оно – кодовое слово. Принимаем решение, что оно передано без ошибок.

Получено слово 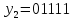. В таблице смежных классов оно располагается в третьей строке и в третьем столбце. Принимаем решение, что было передано слово 01011 с ошибкой в третьем информационном разряде.

7.б. Получено слово . ⇒ ошибок нет

Получено слово . - комбинация 01 соответствует третьей строке транспонированной проверочной матрицы, что означает, что ошибка произошла в третьем информационном разряде.

8.а.

символ	а	б	с	д	е	и	к	р	т
частота	10	11	3	6	9	8	5	7	1

, , , ,

, , , ,

, .

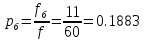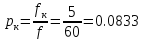б	0,1833	0,1833	0,1833	*0,2167	*0,2833	*0,3167	*0,4	*0,6	*1
а	0,1667	0,1667	0,1667	0,1833	0,2167	0,2833	0,3167	0,4
е	0,15	0,15	0,15	0,1667	0,1833	0,2167	0,2833
и	0,1333	0,1333	*0,15	0,15	0,1667	0,1833
р	0,1167	0,1167	0,133	0,15	0,15
д	0,1	0,1	0,1167	0,1333
к	0,0833	0,0833	0,1
с	0,05	*0,0667
т	0,0167

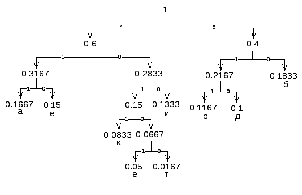
8.б.

Символ	а	б	с	д	е	и	к	р	т
Вероятность	0,1667	0,1833	0,05	0,1	0,15	0,1333	0,0833	0,1167	0,0167
Код	111	00	10101	010	110	100	1011	011	10100

9.

номера отсчетов берутся по модулю N=7.

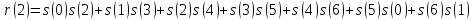
10.

Алгоритм Горнера:

Произвольный полином степени N: . Представим полином p(z) в виде 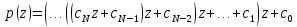. Вычисление начнем с произведения , затем суммы , далее произведения и т.д. Метод Горнера требует не более N операций умножения и N операций сложения.

Пример: пусть дан полином p(z) степени N = 5: p(z) = z⁵ - 2z⁴ + z³ - z² + 4z + 4.

p(z) = (z⁴ - 2z³ + z² – z + 4)z + 4 = ((z³ - 2z² + z - 1)z + 4)z + 4 = (((z² – 2z + 1)z – 1)z + 4)z + 4 =

= ((((z – 2)z + 1)z – 1)z + 4)z + 4.

Пусть z = 1: z - 2 = 1 - 2 = -1, -1 · z = -1·1 = -1, –1 + 1 = 0, 0 · z = 0, 0 - 1 = -1, -1 · z = -1, -1 + 4 = 3, 3 · z = = 3 · 1 = 3, 3 + 4 = 7. Мультипликативная сложность = 4, аддитивная = 5. Если бы полином считался прямо, то мультипликативная сложность составила бы 6 операций умножения.

Вычисление полинома в точках с помощью алгоритма «разделяй и властвуй»:

Пусть необходимо вычислить полином в нескольких точках а₁, а₂, …, а_k, k ≤ N. Положим сначала

z = a₁. Тогда можно записать p(z) = (z – a₁) q(z) + r(z), где q(z) и r(z) – частное и остаток от деления p(z) на (z – a₁). Этот результат можно распространить на большее число точек. Рассмотрим произведение и запишем p(z) = m(z) q(z) + r(z). В точке z = a_i полином m(z) равен нулю, поэтому p(a_i) = r(a_i). Теперь вычисление полинома p(z) свелось к вычислению полинома r(z), степень которого меньше.

Этот подход можно использовать для построения алгоритма вычисления полинома степени N – 1 в N точках. Положим N = 2^l. Разделим N точек на две половины и образуем полиномы

и . Разделим p(z) на m₁(z) и m₂(z). При этом получим остатки r₁(z) и r₂(z) степени N/2. Теперь осталось вычислить эти остатки в N/2 точках. Для вычисления остатков можно воспользоваться аналогичным приемом, повторяя его многократно.

Пример: Пусть требуется вычислить полином p(z) = 5z³ – 2z² + 2z - 4 в точках z, равных -2, 0, -1, 1.

Образуем m₁(z) = (z + 2)z = z² + 2z, m₂(z) = (z – 1)(z + 1) = z² – 1. После деления p(z) на m₁(z) и m₂(z) получим остатки r₁(z) = 26z - 4, r₂(z) = 7z – 6. Разделив r₁(z) на z + 2 и z, запишем p(-2) = -56, p(0) = -4. Аналогично, разделив r₂(z) на z – 1 и z + 1, найдем p(1) = 1, p(-1) = -13.