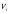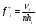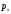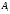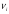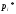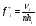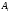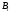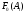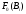Контрольна по ТВиМС

1.9. Телефонный номер состоит из шести цифр, каждая из которых равновозможно принимает значения от 0 до 9. Найти вероятность того, что все цифры одинаковы.

1.11. Условие задачи 1.9. Вычислить вероятность того, что номер не содержит цифры пять.

Решение.

Обозначим событие А- событие состоящее в том, что номер не содержит цифры 5.

Для нахождения вероятности события А воспользуемся классическим определением вероятности

Р(A)=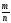

Где 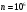– общее число всевозможных номеров (число перестановок с повторениями 10 цифр по 6 местам)

m=9⁵=59049 – число номеров в которых нет пятерки (число перестановок с повторениями 9 цифр по 5 местам)

тогда

Р(A)=59049/1000000=0,0590

Ответ: Р(A)=0,0590

В задачах 2.1-2.40 приведены схемы соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.

№2,11

р₁=0,1 р₂=0,2 р₃=0,3 р₄=0,4

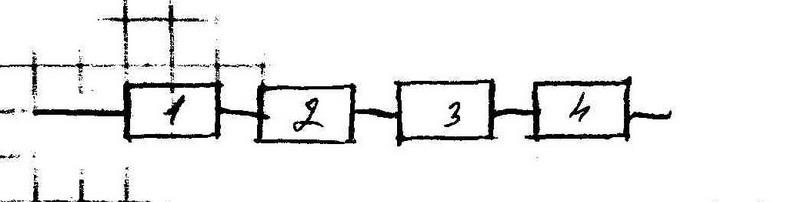
Обозначим А_i – событие состоящее в том, что i-ый элемент работает. В – событие состоящее в том, что сигнал пройдет через цепь.

В=А₁А₂А₃А₄

Так как события А_i независимы, то

Р(В)=Р(А₁)р(А₂) р(А₃) р(А₄)=(1-р₁)(1-р₂)(1-р₃)(1-р₄)

Р(В)=(1-0,1)(1-0,2)(1-0,3)(1-0,4)=0,9*0,8*0,7*0,6=0,3024,

Ответ: Р(В)=0,3024

3.11. Группа студентов состоит из пяти отличников, десяти хорошо успевающих и семи занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность того, что студент получит хорошую или отличную оценку.

Решение.

Обозначим А – событие состоящее в том, что в студент получит хорошую или отличную оценку

Можно выдвинуть три гипотезы

Н₁– вызвали отличника

Р(Н₁)=5/22

Н₂– вызвали хорошо успевающих

Р(Н₂)=10/22

Н₃– вызвали слабо успевающих

Р(Н₃)=7/22

Условная вероятность того, что отличник сдаст на хорошо или отлично

Р_Н1(А)=1

Хорошо успевающий

Р_Н2(А)=1

Слабо успевающий

Р_Н3(А)=1/3

Вероятность события А найдем по формуле полной вероятности

Р(А)= Р(Н₁)* Р_Н1(А)+ Р(Н₂)* Р_Н2(А)+ Р(Н₃)* Р_Н3(А)

Р(А)=5/22*1+10/22*1+7/22*(1/3)=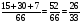

Ответ: Р(А)=26/33

4.11. Монету подбрасывают восемь раз. Чему равно наивероятнейшее число выпадений герба?

Решение.

р=0,5-вероятность выпадения герба при одном броске, n=8- число бросков

Наивероятнейшее число стандартных деталей найдем по формуле

np-q≤k<np+p

0,5*8-0,5≤k<8*0,5+0,5

3,5≤k<4,5

k=4

Ответ: к=4

ЗАДАЧА 5

В задачах 5.1-5.30 дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в табл. 1.1). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

№5,11

Х	0	1	2	3	4
Р	0,1	0,2	0,3	0,4	0

Математическое ожидание

М(Х)=

М(Х)= 0*0,1+1*0,2+2*0,3+3*0,4+4*0=2,0

Дисперсия

Д(Х)=М(Х²)–( М(Х))²

Где М(Х²)=

М(Х²)= 0²*0,1+1²*0,2+2²*0,3+3²*0,4+4²*0=5

Д(Х)=5–2²=1

Функция распределения

F(x_i)=P{X<x_i}=P{(X=x₁)(X=x₂) ... (X=x_i-1)}= p₁+...+p_i-1.

F(X)=

График функции распределения

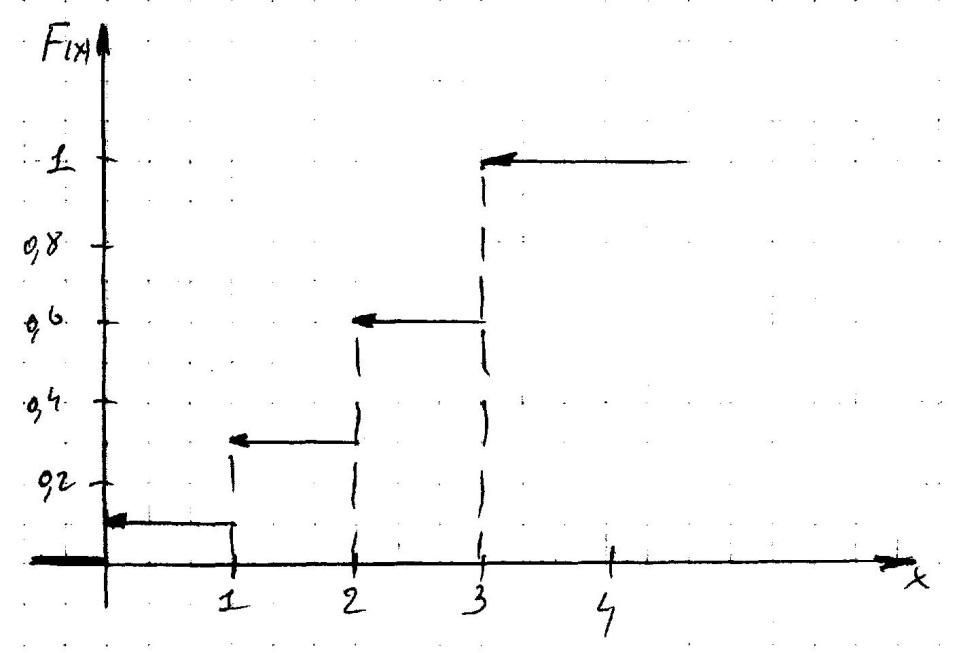
ЗАДАЧА 6

В задачах 6.1-6.30 (параметры заданий приведены в табл. 1.2) случайная величина Х задана плотностью вероятности

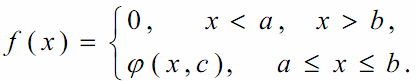
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал [α, β].

№6.11

f(x)=

Для определения постоянной с воспользуемся свойством плотности вероятности

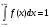
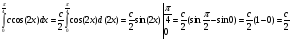
с/2=1

с=2

f(x)=

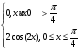
математическое ожидание

М(Х)=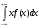

М(Х)=

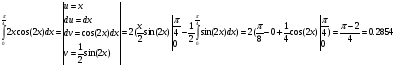
Дисперсия

Д(Х)=М(Х²)–(М(Х))²

Где М(Х²)=

=

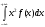
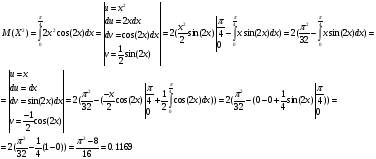Д(Х)=0,1169–0,2854² =0.0354

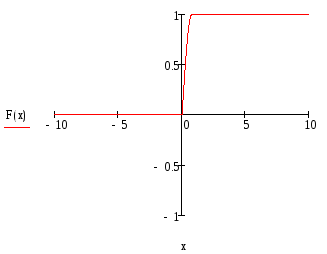
Функция распределения

F(x)=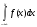

F(X)= при x<0

F(X)=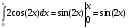 при 0≤x≤

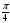F(X)= при <x

F(X)=

Вероятность того, что 0,5<x<1 найдем по формуле

Р(0,5<x<1)=

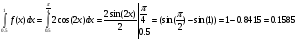
ЗАДАЧА 7

В задачах 7.1-7.30 (условия приведены в табл. 1.3) случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=ϕ(X) и определить плотность вероятности g(y).

№7.11

Y=2х

Плотность вероятности СВ Х найдем по формуле

f(x)=,

f(x)=1/(6+4)=0.1

График функции Y=2х при -4≤x≤6

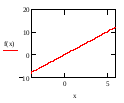
x=0.5y

х’=(0.5y)’=0.5

g(y)=f(0.5y)*(0.5)=0.1*0.5=0.05

_{свойство плотности вероятности}

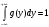
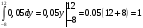
Ответ: g(y)=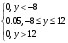

ЗАДАЧА 8.

В задачах 8.1-8.30 (конкретные параметры приведены в табл. 1.4) двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 1.1 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

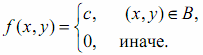
Вычислить коэффициент корреляции между величинами X и Y.

№8.11

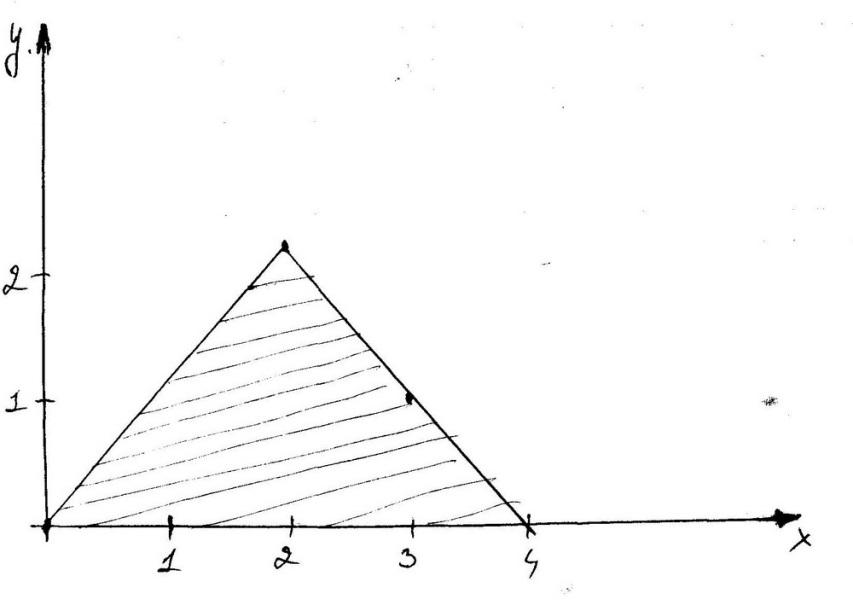
y=x

y=4-x

Коэффициент корреляции

r=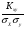

плотность распределения СВ (x,y) найдем по формуле

f(x,y)=1/S

где S–площадь фигуры

S=0.5*2*4=4

f(x,y)=1/4

Плотность распределения f(x) найдем по формуле

f(x)=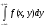

f(x)= 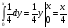, 0<x≤2

f(x)= , 2<x≤4

f(x)=

f(y)=

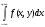
f(y)= ,0<y≤2

f(y)=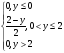

Математическое ожидание

М(Х)=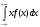

М(Y)=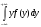

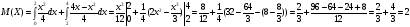
М(Y)=

К=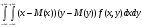

Среднее квадратическое отклонение

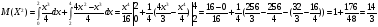
М(Y²)=

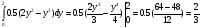
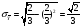
r=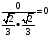

r=0

Ответ: r=0

ЗАДАЧА 9.

В задачах 9.1-9.30 вычислить математическое ожидание и дисперсию величин U и V, а так же определить их коэффициент корреляции R_UV:

U = a₀ +a₁X₁ +a₂X₂ V = b₀ + b₁X₂ + b₂X₃ .

Конкретные значения коэффициентов a_i, i = 0, ..., 2; b_j, j = 0, ..., 2 и числовые характеристики случайных величин X_i, i = 0, ..., 3 приведены в табл. 1.9.

№9,11

Решение:

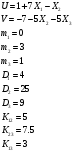
Коэффициент корреляции найдем по формуле

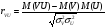
Воспользуемся свойством математического ожидания

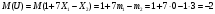
_{Дисперсия}

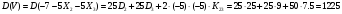
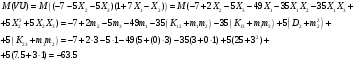
Коэффициент корреляции

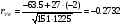
2. КОНТРОЛЬНЫЕ ЗАДАЧИ ТИПОВОГО РАСЧЕТА ПО

МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

В данном разделе приведены задания по статистической обработке и анализу одномерных (задача №10) и двумерных (задача №11) случайных величин.

ЗАДАЧА 10.

По выборке одномерной случайной величины:

- получить вариационный ряд;

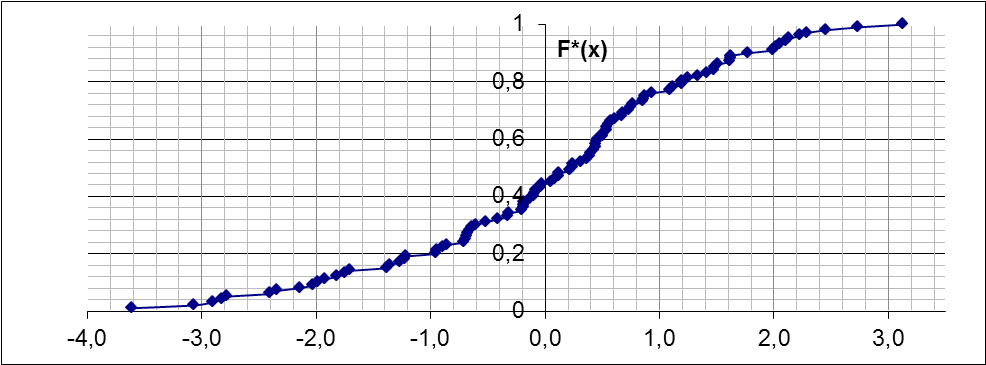
- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x);

- построить гистограмму равноинтервальным способом;

- построить гистограмму равновероятностным способом;

- вычислить оценки математического ожидания и дисперсии;

- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия χ² и критерия Колмогорова (α = 0,05).

№10,11

Вариационный ряд

-3,61	0,24
-3,07	0,31
-2,91	0,36
-2,83	0,39
-2,78	0,40
-2,41	0,42
-2,35	0,44
-2,15	0,44
-2,03	0,45
-1,99	0,46
-1,93	0,50
-1,82	0,51
-1,75	0,54
-1,71	0,54
-1,39	0,55
-1,36	0,57
-1,27	0,61
-1,23	0,67
-1,22	0,68
-0,96	0,73
-0,95	0,75
-0,9	0,76
-0,86	0,85
-0,71	0,86
-0,7	0,87
-0,69	0,93
-0,68	1,09
-0,66	1,11
-0,64	1,19
-0,61	1,19
-0,52	1,24
-0,42	1,33
-0,33	1,41
-0,32	1,47
-0,21	1,48
-0,19	1,51
-0,19	1,61
-0,19	1,62
-0,14	1,62
-0,1	1,77
-0,09	1,99
-0,08	2,01
-0,04	2,05
-0,03	2,10
0,05	2,13
0,08	2,22
0,12	2,28
0,12	2,45
0,21	2,73
0,24	3,12

Эмпирическая функция распределения

По формуле 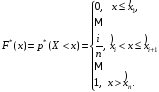построим график эмпирической функции распределения 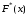. Так как 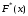является неубывающей функцией и все ступеньки графика 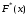имеют одинаковую величину 1/n (или ей кратны – для одинаковых значений), то таблицу значений эмпирической функции распределения F*(x) можно не вычислять, а построить ее график непосредственно по и вариационному ряду, начиная с его первого значения

Количество интервалов M, необходимое для построения гистограмм, определим по объему выборки ( см. формулу (10.2)):

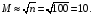
Для равноинтервальной гистограммы величины h_j, A_j, B_j, рассчитаем по формуле 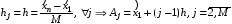и заполним все колонки интервального статистического ряда :

Шаг интервала

h=

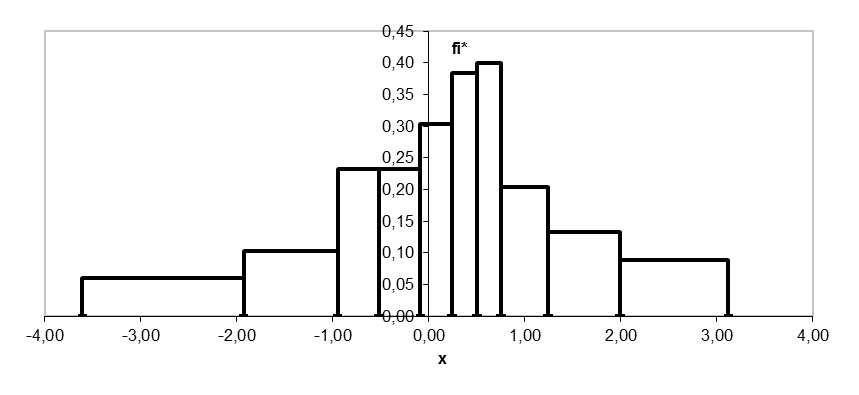
h=(3,12+3,61)/10=0.673

-3,610	-2,937	0,673	2	0,02	0,030	0,02
-2,937	-2,264	0,673	5	0,05	0,074	0,07
-2,264	-1,591	0,673	7	0,07	0,104	0,14
-1,591	-0,918	0,673	7	0,07	0,104	0,21
-0,918	-0,245	0,673	13	0,13	0,193	0,34
-0,245	0,428	0,673	22	0,22	0,327	0,56
0,428	1,101	0,673	21	0,21	0,312	0,77
1,101	1,774	0,673	13	0,13	0,193	0,9
1,774	2,447	0,673	7	0,07	0,104	0,97
2,447	3,120	0,673	3	0,03	0,045	1

Гистограмма равноинтервальным способом

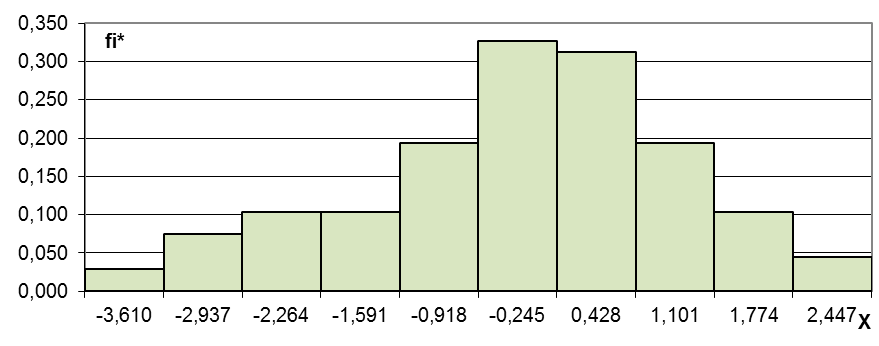
Гистограмма равновероятностным способом

-3,610	-2,937	1,68	10	0,1	0,060
-2,937	-2,264	0,98	10	0,1	0,102
-2,264	-1,591	0,43	10	0,1	0,233
-1,591	-0,918	0,43	10	0,1	0,233
-0,918	-0,245	0,33	10	0,1	0,303
-0,245	0,428	0,26	10	0,1	0,385
0,428	1,101	0,25	10	0,1	0,400
1,101	1,774	0,49	10	0,1	0,204
1,774	2,447	0,75	10	0,1	0,133
2,447	3,120	1,13	10	0,1	0,088

Вычислим точечную оценку математического ожидания по формуле:

.

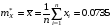Вычислим точечную оценку дисперсии по формуле:

.

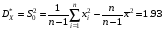Построим доверительный интервал для математического ожидания с надежностью γ = 0,95 по формуле .

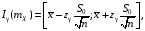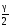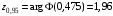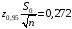Для этого в таблице функции Лапласа найдем значение, равное = 0,475, и определим значение аргумента, ему соответствующее: . Затем вычислим и получим доверительный интервал для математического ожидания:

.

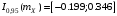Построим доверительный интервал для дисперсии с надежностью γ = 0,95 по формуле .

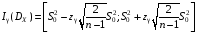Вычислим и получим доверительный интервал для дисперсии:

.

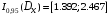По виду гистограммы выдвинем гипотезу о нормальном распределении СВХ. Проверим гипотезу о нормальном распределении СВХ при помощи критерия χ²

Н₀: F(x)=F₀(x),

Н₁: F(x)≠F₀(x),

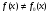
Где F₀(x), 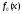– теоретическая функция и плотность распределения

,

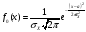Где

,

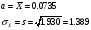
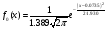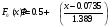
χ²=

	-2,937	0	0,0139	0,0139	0,02	0,00267
-2,937	-2,264	0,0139	0,0433	0,0294	0,05	0,01437
-2,264	-1,591	0,0433	0,1100	0,0667	0,07	0,00017
-1,591	-0,918	0,1100	0,2297	0,1197	0,07	0,02064
-0,918	-0,245	0,2297	0,4001	0,1704	0,13	0,00957
-0,245	0,428	0,4001	0,5924	0,1923	0,22	0,00400
0,428	1,101	0,5924	0,7643	0,1720	0,21	0,00841
1,101	1,774	0,7643	0,8863	0,1220	0,13	0,00053
1,774	2,447	0,8863	0,9548	0,0686	0,07	0,00003
2,447		0,9548	1	0,0452	0,03	0,00509
			сумма	1	1	0,06548