контрольная работа

Министерство образования Республики Беларусь

Учреждение образования

«Белорусский Государственный университет

информатики и радиоэлектроники»

Факультет непрерывного и дистанционного обучения

КОНТРОЛЬНАЯ РАБОТА №1

по дисциплине

Теория вероятностей и математическая статистика

Вариант № 5

Выполнил студент

Чак Наталья Николаевна

Группа №802321С, шифр № 05

E-mail: nataliamax@tut.by

Дата 2011-04-20

2011

Задача 1(3).

Подбрасываются две игральные кости. Определить вероятность того, что сумма выпавших чисел превышает 10.

Решение.

Равновозможными элементарными исходами здесь являются пары (x, y), где x и y принимают значения: 1,2,3,4,5,6. Таким образом, общее число элементарных исходов равно n = 6 * 6 = 36.

Событию А благоприятствуют пары (5;6), (6;6), (6;5), число которых равно m = 3.

Следовательно, Р(А) = m/n = 3/36 = 0,83+

Задача 2(39)

Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5, 6 соответственно равны q₁=0,1; q₂=0,2; q₃=0,3; q₄=0,4; q₅=0,5 q₆=0,6 . Найти вероятность того, что сигнал пройдет со входа на выход.

1 2 3

Решение.

А_i – работает i-ый элемент;

- не работает i-ый элемент

=

=(0,9*0,7+0,8*0,6-0,9*0,8*0,7*0,6)*(0,5+0,4-0,5*0,4)=0,5653+

Задача 3(27)

Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором - 10 белых и 10 черных шаров, в третьем - 20 черных шаров. Из каждого ящика вынули шар. Затем из этих трех шаров наугад взяли один шар. Вычислить вероятность того, что шар белый.

Решение.

А = {вынутый шар - белый};

В_i = {шар вынули из i-го ящика};

p(B₁)=20/60=1/3; p(B₂)=1/3; p(B₃)=1/3 .

p(A/B₁)=1; p(A/B₂)=1/2; p(B₃)=0 .

По формуле полной вероятности

p(A)=p(B₁)*p(A/B₁)+p(B₂)*p(A/B₂)+p(B₃)*p(A/B₃)=

=1/3 * 1 + 1/3 * 1/2 + 1/3 * 0 =0.5

Задача 4(21)

Монету подбрасывают восемь раз. Какова вероятность того, что она четыре раза упадет гербом вверх?

Решение.

Вероятность выпадения монеты гербом вверх p=1/2. По формуле Бернулли

n=8, k=4, p=1/2, q=1 - p=1/2

+

Задача 5(7)

Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в таблице). Найти p отмеченные *. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

Таблица. 5.1

Вариант	x1	x2	x3	x4	x5	p1	p2	p3	p4	p5
5.7	-5	-2	0	1	2	0,5	0,1	0,1	0,2	0,1

Решение.

Математическое ожидание:

Дисперсия

Определяем функцию распределения

Строим график:

+

Задача 6(22)

Случайная величина Х задана плотностью вероятности

Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал.

Вариант	x,c)	a	B		
6.22	c x10	-1	1	-0,5	0,5

Решение.

Константу с вычислим исходя из условия нормировки

Математическое ожидание:

Дисперсия:

Функция распределения:

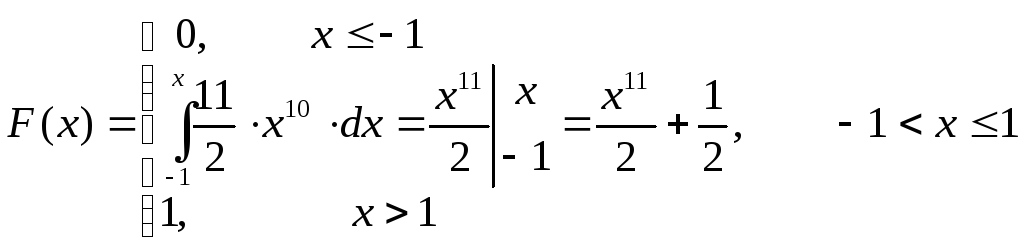
Вероятность попадания в интервал (-0,5; 0,5) будет:

+

Задача 7(11)

Случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).

Вариант		a	b
7.11		-4	6

Решение.

Так как X равномерно распределено на интервале [-4; 6], то ее плотность вероятности:

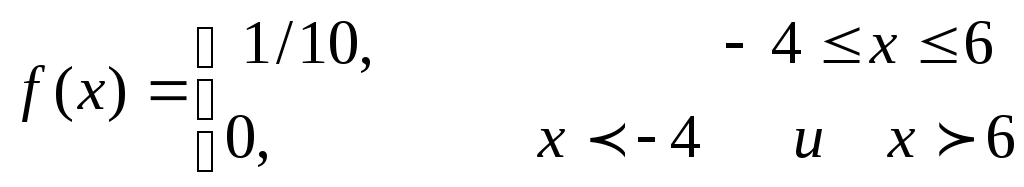
Строим график величины y=2x в интервале [-4; 6] и в зависимости от числа k обратных функций выделим следующие интервалы для y:

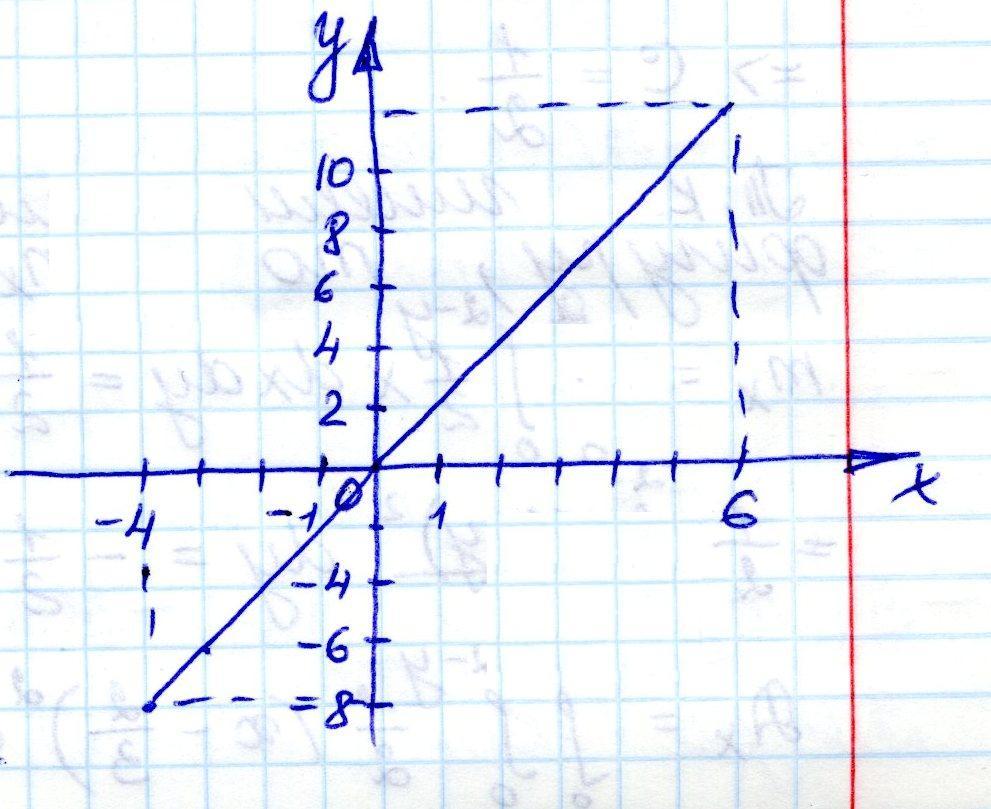[-∞; -8] k=0

[-8; 12] k=1

[12; +∞] k=0

Для интервалов (-∞; -8) и (12; -∞) g(y)=0

Для интервалов [-∞; 12] g(y)=y/2

Тогда получаем

+

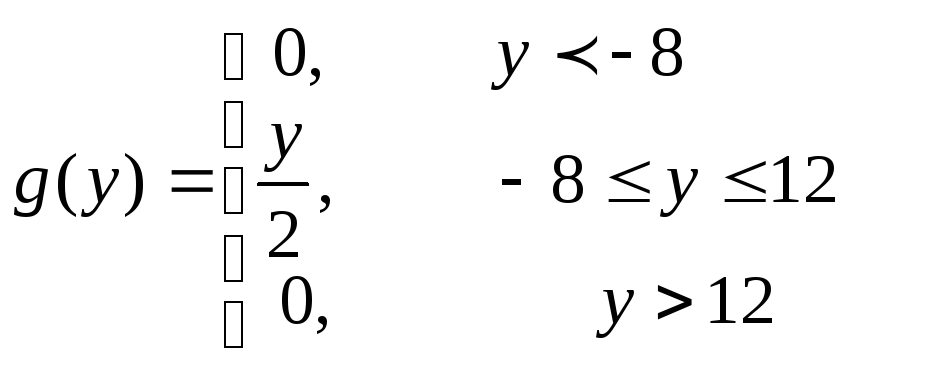
Задача 8(31)

Двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рисунке области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

Вычислить коэффициент корреляции между величинами X и Y.

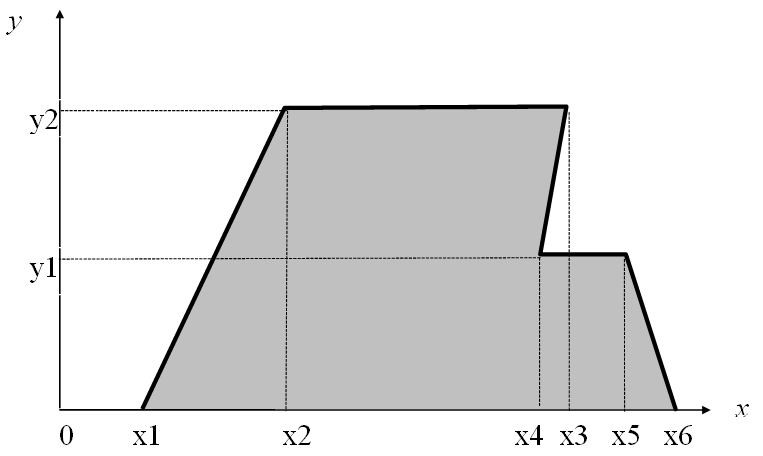
Вариант	x1	x2	x3	x4	x5	x6	y1	y2
8.31	0	0	0	1	1	2	1	2

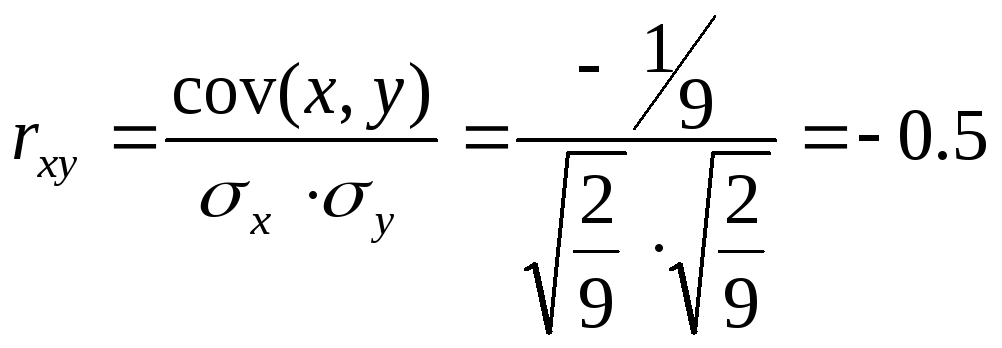
Решение.

Плотность вероятности будет

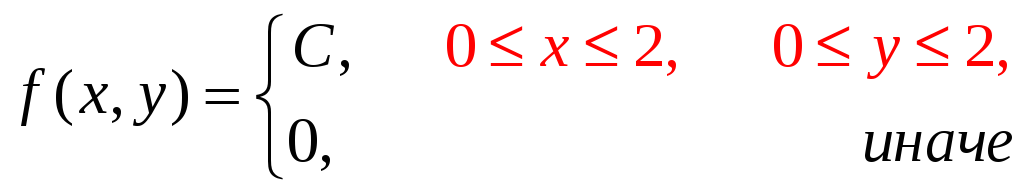
Определим С:

Так как имеем симметричную фигуру, то m_x=m_y; Д_x=Д_у;

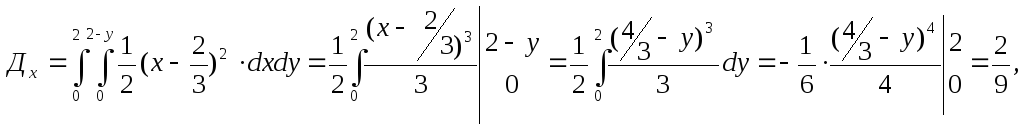
Коэффициент корреляции

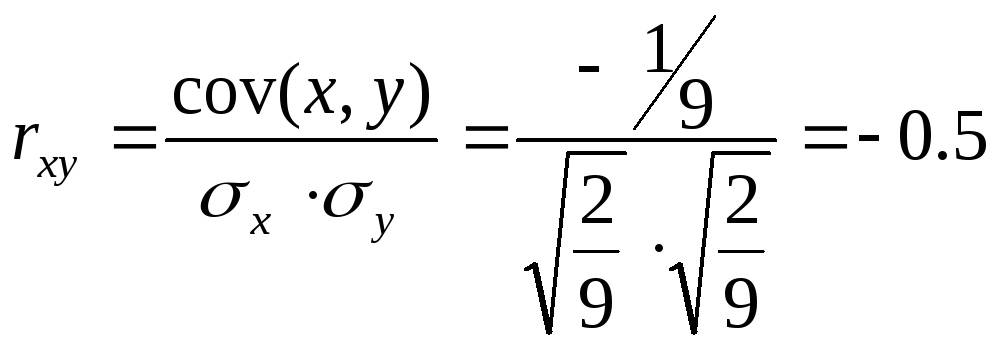
Задача 9(9)

Вычислить математическое ожидание и дисперсию величин U и V, а так же определить их коэффициент корреляции :

.

Конкретные значения коэффициентов и числовые характеристики случайных величин приведены в таблице

Таблица

Вариант	a0	a1	a2	b0	b1	b2	m1	m2	m3	D1	D2	D3	K12	K23	K13
9.9	-1	7	1	-9	-7	-3	0	5	1	4	16	4	4	4	0

Вычислим математические ожидания U и V:

m_U=-1+7 m₁+ m₂=4;

m_V=-9-7 m₂-3 m₃=-47;

Вычислим дисперсии U и V:

Вычислим корреляционный момент K_UV

Тогда

Величина R_UV будет:

+