
Пример контрольной работы
.pdf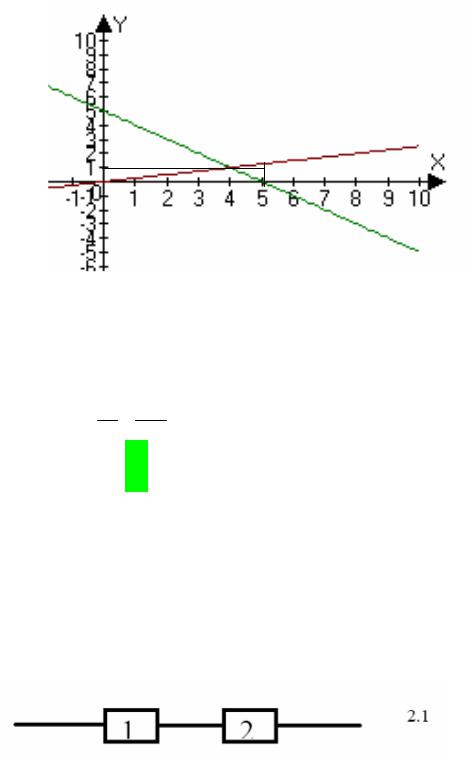
ЗАДАЧА 1.
В задачах 1.13-1.19 наудачу взяты два положительных числа x и y, причем x ≤ 5, y ≤ 2. Найти вероятность того, что y+ax-b ≤ 0 и y-cx ≤ 0.
1.15. a=1, b=5, c=0,25.
Решение:
Требуется найти вероятность того, что y+ax–b ≤ 0 и y-cx ≤ 0 ,
или y ≤ 5-x и y ≤ 0.25x.
K B
A
0
C
Площадь прямоугольника ОАВС равна S1=1×5=5;
Точки удовлетворяющие неравенствам y ≤ 5-x и y ≤ 0.25x принадлежать треугольнику ОКС. Площадь треугольника составляет
S2= 12 ×4 ×1 + 12 ×1(5 − 4)= 2 + 12 = 2,5 P(A)= SS12 = 2 ×5 5 = 12
Ответ: 12 .+
ЗАДАЧА 2.
В задаче 2.1 приведены схемы соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2 соответственно равны p1=0,1; p2=0,2. Найти вероятность того, что сигнал пройдет со входа на выход.
Решение:

Цепь из элементов при последовательном подключении выходит из строя при отказе хоть одного элемента.
Тогда вероятность выхода из строя равна:
P(A1 + A2) = 0,1 + 0,2 −0,1×0,2 = 0,3 −0,02 = 0,28
А вероятность того, что сигнал пройдет с входа на выход:
P(A) =1 −0,28 = 0,72
Ответ: 0,72. +
3.12. Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором - 10 белых и 10 черных шаров, в третьем - 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.
Решение:
Полагая k = 1 – одна урна с благоприятным исходом, n = 3 – всего три.
P(Hi / A) = |
|
P(H1 )P(A / H1 ) |
|
|
|
||||
|
P(H1 )P(A / H1 ) + P(H2 )P(A / H2 ) + P(H3 )P(A / H3 ) |
|
|||||||
Найдем соответствующие вероятности: |
|
|
|||||||
Р(Н1)=1/3 |
|
Р(Н2) = 1/3 Р(Н3) = 1/3 |
|
|
|
||||
Р(А/Н1) = 20/20 =1 |
|
Р(А/Н2) = 10/20 |
Р(А/Н3) = 0 |
||||||
Учитывая |
|
независимость событий, найдем условную вероятность ис- |
|||||||
пользуя формулой Бейеса: |
|
|
|
|
|
|
|
||
P(H1 / A) = |
|
1/ 3×1 |
= |
|
1/ 3 |
|
= 1×6 = |
2 |
|
1/ 3×1 +1/ 3×1/ 2 + 0 |
1/ 3 +1/ 6 |
|
|
|
|||||
|
|
|
3×3 3 |
|
|||||
Ответ: 2/3. +
ЗАДАЧА 4.
4.4. Игральную кость подбрасывают 12 раз. Чему равно наивероятнейшее число выпадений 6?
Решение:
Благоприятный исход одного броска равен 1/6.
По свойству формулы Бернулли, число k0 которому соответствует максимальная вероятность P(n,k0), называется наивероятнейшим числом появления события А и определяется неравенствами:
np − q ≤ k0 ≤ np + p
12× 16 − 65 ≤ k0 ≤12× 16 + 16 1.16 ≤ k0 ≤ 2.16
Итак, при k≥1.16 функция возрастает, а при k≤2.16 – убывает. Тогда существует точка k0, в которой P(n,k) достигает максимума.
Таким образом – наивероятнейшее число выпадений 6 равно двум.

Ответ: 2. . +
ЗАДАЧА 5.
В задачах 5.20 дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в табл. 1.1). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
Вариант |
x1 |
x2 |
x3 |
x4 |
x5 |
p1 |
p2 |
p3 |
p4 |
p5 |
5.20 |
5 |
6 |
7 |
8 |
9 |
0,1 |
0,1 |
0,1 |
0,1 |
0,6 |
Решение:
Представим исходные данные в виде таблицы:
X |
5 |
6 |
7 |
8 |
9 |
P |
0,1 |
0,1 |
0,1 |
0,1 |
0,6 |
Вычислим математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение σ(Х).
n
M (x) = ∑xi pi .
i=1
М(X)=5×0,1+6×0,1+7×0,1+8×0,1+9×0,6=8;
D(x) = M (x2 ) −[M (x)]2 ;
n
M(x2 ) = ∑x2i pi .
i=1
M (x2 ) =25×0,1+36×0,1+49×0,1+64×0,1+81×0,6=66; D(x) =66–82=2
σ(x) = D(x) =1,41;
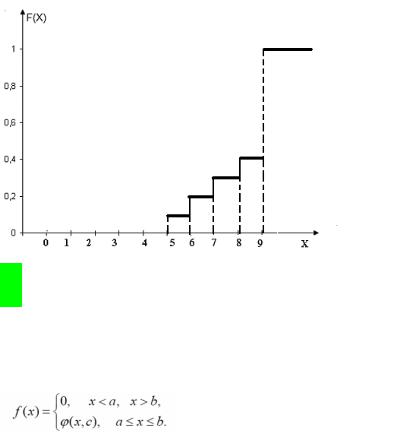
Рассчитаем и построим график функции распределения. Следовательно, функция распределения будет иметь вид
|
0, |
x ≤ 5 |
0,1; |
5 ≤ x ≤ 6 |
|
F(x) = 0,2; |
6 ≤ x ≤ 7 |
|
0,3; |
7 ≤ x ≤ 8 |
|
0,4; |
8 ≤ x ≤ 9 |
|
|
|
|
|
0,1; 9 ≤ x |
|
|
||
Построим график функции распределения
+
ЗАДАЧА 6.
В задачах 6.15 (параметры заданий приведены в табл. 1.2) случайная величина Х задана плотностью вероятности
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интер-
вал[α, β].
Таблица 1.2
Вариант |
φ(x,c) |
|
a |
|
b |
|
α |
β |
||||
6.15 |
cx |
|
|
|
|
|
-2 |
|
2 |
|
1,5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
x < −2 |
|
|||||||||
|
|
0, |
|
|
||||||||
|
|
|
x |
|
, |
- 2 ≤ x ≤ 2 |
|
|||||
|
|
|
|
|||||||||
f (x) = C |
|
|
|
|||||||||
|
|
0, |
x > 2 |
|
|
|||||||
|
|
|
|
|||||||||
По свойству вероятности ∞∫ f (x)dx =1, учитывая что при х<-2 и х>2 f(x)=0 по-
−∞
лучим.
⌠ |
2 |
|
|
|
|
|
|
C |
x |
dx = 4 C |
|||
⌡− 2 |
|
|
|
|
=> C = 1/4 |
|
|
|
|
|
0, |
x < −2 |
|
|
|
|
1 |
, |
- 2 ≤ x ≤ 2 |
|
f (x) = |
||||||
|
|
|
4 |
0, |
x > 2 |
|
|
|
|
|
|||

|
⌠2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
M[x] = |
|
|
x |
|
x |
|
dx = 0 |
||||||||||
|
|||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
⌡− 2 |
|
|
|
|
|
|
|
|||||||||
|
⌠2 |
|
x2 1 |
|
|
|
|
|
dx − (0)2 = 2 |
||||||||
D[x] = |
|
|
|
|
|
x |
|||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
⌡− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функция распределения с плотностью распределения связаны форму- |
|||||||||||||||||
лой F(x) = ∫x |
f (t)dt |
|
|
|
|
|
|
|
|||||||||
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
f(x) ≠ 0 только для − 2 ≤ x ≤ 2 , то по свойствам F(x) имеем: |
||||||||||||||||
F(x)=0 при x<–2; F(x) = 1 при x>2. Для − 2 ≤ x ≤ 2 : |
|||||||||||||||||
F(x) = ∫x 1 |
|
t |
|
dt = |
x2 |
|
|||||||||||
|
|
||||||||||||||||
|
|
|
|||||||||||||||
|
0 |
4 |
|
|
|
|
|
|
|
8 |
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0, |
|
|
|
x < −2 |
|||||||||
F(x) = |
x2 |
|
, |
|
|
- 2 ≤ x ≤ 2 |
|||||||||||
|
|
|
|
|
|
||||||||||||
8 |
|
|
|
|
|||||||||||||
|
|
|
1, |
|
|
|
x > 2 |
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность попадания случайной величины в заданный интервал (α, β) можно найти по формуле: Р(α<=x<β) = F(β)–F(α).
P(1.5<=x<=2)=F(2)–F(1.5)= 4/8 – 2.25/8 = 0.209
+
ЗАДАЧА 7.
В задаче 7.15 (условия приведены в табл. 1.3) случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=φ(X) и определить плотность вероятности g(y).
Таблица 1.3
Вариант |
φ (x) |
a |
b |
|
|
|
|
7.15 |
sin(x) |
0 |
0,75π |
|
|
|
|
Решение:
Так как случайная величина распределена равномерно на интервале [0, 0.75π], то ее плотность распределения имеет вид:
|
|
0, |
|
x < a |
||
|
1 |
|
|
|
a ≤ x ≤ b , |
|
f (x) = |
|
, |
|
|||
|
|
|
||||
b − a |
|
|
x > b |
|||
|
|
0, |
|
|||
или |
|
|
|
0, |
x < 0 |
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
f (x) = |
|
|
|
, |
0 ≤ x ≤ 0.75π |
|
|
0.75π |
|||||
|
|
x > 0.75π |
||||
|
|
0, |
|
|||
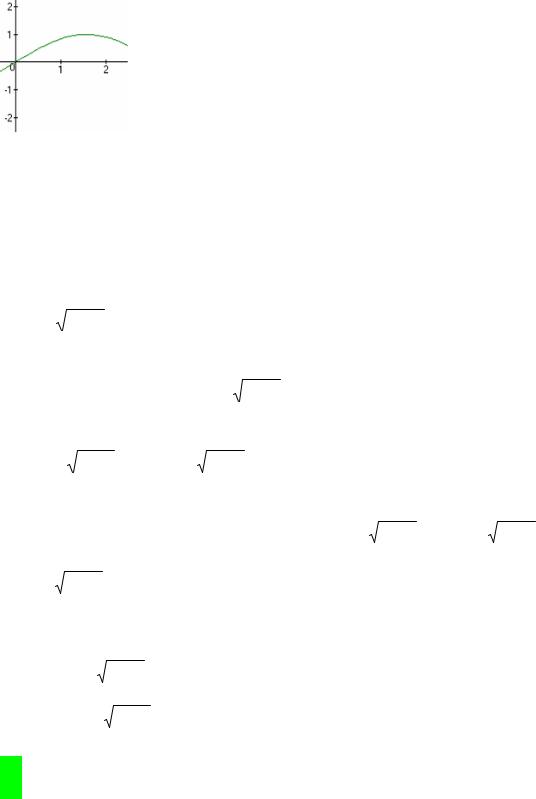
Построим график величины Y=sin(x) для x в интервале [0, 0.75π] и в зависимости от числа k обратных функций выделим следующие интервалы для Y:
[-∞, 0] k=0 [0, 0.5] k=1 [0.5, 1] k=2 [1, +∞] k=0
Так как на интервале [-∞, 0] и [1, +∞] обратная функция не существует, то для этих интервалов g(y)=0;
В интервале [0, 0.5] имеется одна обратная функция ψ( y) = −arcsin(y);
′ |
1 |
|
1− y2 |
||
ψ ( y) = |
По формуле получим:
g( y) = |
fx (ψ( y)) × |
|
ψ |
′ |
|
= |
1 |
× |
|
1 |
|
|
|
||||||||
|
|
|
|
|
||||||
|
( y) |
|
0.75π |
|
− y2 |
|||||
|
|
|
|
|
|
|
1 |
|||
В интервале [0.5, 1] две обратные функции:
ψ1′( y) = − |
|
1 |
|
|
|
и ψ2′( y) = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1− y2 |
|
|
− y2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
По формуле получим: |
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|||||||||||||||
g( y) = fx |
(ψ1( y)) |
× |
|
ψ1′( y) |
|
+ fx (ψ2 |
( y)) × |
|
ψ2′( y) |
|
= |
× |
|
+ |
× |
|
= |
||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
0.75π |
|
|
0.75π |
|
|
||||||||||||||||||||||
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− y2 |
|
1 |
− y2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0.75π |
1− y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом плотность вероятности величины Y равна: |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
0, |
|
|
|
|
|
|
|
y < 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
, 0 ≤ y ≤1/ 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
0.75π |
|
1− y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
g( y) = |
|
|
2 |
|
|
|
|
|
|
|
1/2 ≤ y ≤1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0.75π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1− y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
y >1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
+
ЗАДАНИЕ 8 (22).
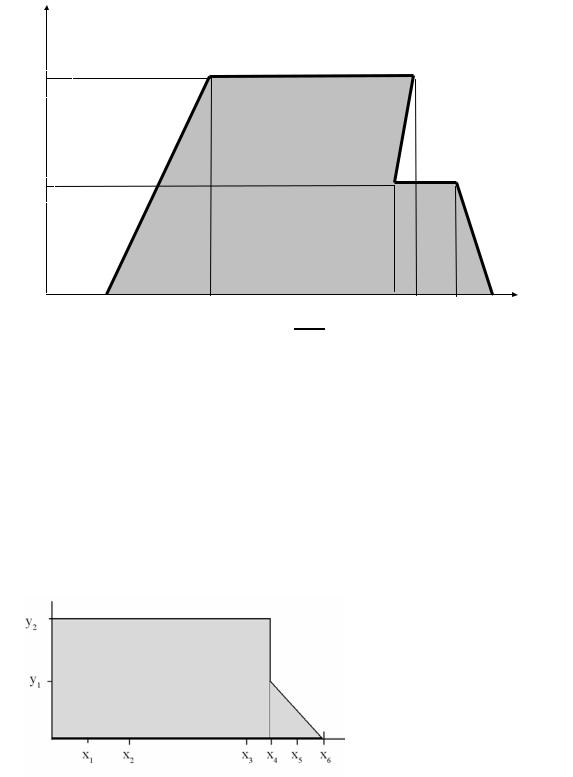
В задаче 8 двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 1.1 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
c, (x, y) B, f (x, y) =
0, иначе.
Вычислить коэффициент корреляции между величинами X и Y.
Рис. 1.1
y
y2
y1
x
0 |
x1 |
x2 |
|
|
|
|
x3 |
x4 |
x5 |
x6 |
||
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
Вариант |
x1 |
x2 |
x3 |
x5 |
x6 |
y1 |
y2 |
|
|
|
|
|
8.22 |
0 |
0 |
4 |
4 |
4 |
6 |
1 |
2 |
|
|
Решение:
Построим область B. Соединим последовательно точки с координатами согласно рис. 1.1:
-точку (x1;0) = (0;0) c точкой (x2; y2) = (0; 2),
-точку (x2; y2) = (0; 2) c точкой (x4; y2) = (4; 2),
-точку (x4; y2) = (4; 2) c точкой (x3; y1) = (4; 1),
-точку (x3; y1) = (4; 1) c точкой (x5; y1) = (4; 1) (т.е. остаемся на месте),
-точку (x5; y1) = (4; 1) c точкой (x6; 0) = (6; 0) .
В результате получим следующую фигуру:
Запишем в аналитической форме совместную плотность вероятности:

|
|
0 ≤ y ≤ 2;0 ≤ x ≤ 4 |
c, |
≤ y ≤1;4 ≤ x ≤ 6 − 2y |
|
f (x, y) = |
0 |
|
|
|
0,иначе |
|
|
|
Найдем неизвестную константу с, определим, используя условие нормировки плотности вероятности:
∞ ∞ |
2 |
4 |
|
1 |
6−2 y |
|
2 |
1 |
∫ ∫ |
|
|
|
|
|
|
|
|
f (x, y)dxdy = ∫ |
∫cdx dy + ∫ |
∫cdx dy = ∫c ×4dy + ∫c(6 − 2y − 4) = 8c + c = 9c =1 |
||||||
−∞ −∞ |
0 |
0 |
|
0 |
4 |
|
0 |
0 |
с = 19
Проверим геометрически полученный результат. Объем тела, ограниченный поверхностью распределения и плоскостью x0y должен быть равен
единице, т.е. V = c ×Sb = 19 ×9 =1
Вычислим математические ожидания:
|
⌠2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
⌠1 |
|
|
|
|
(6−2 y) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
⌠ |
|
|
1 |
|
|
|
|
|
⌠ |
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
mX := |
|
|
|
|
|
9 x dx dy |
+ |
|
|
|
|
|
|
|
9 |
x dx dy = 2.296 |
|||||||||||||||||||||
|
⌡ ⌡0 |
|
|
|
|
|
|
|
|
|
|
⌡ ⌡4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
⌠2 |
|
|
⌠4 |
|
|
|
|
|
|
⌠1 |
|
|
|
|
⌠6−2 y |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||||||||
mY := |
|
|
|
|
|
9 dx dy + |
|
|
|
|
|
9 dx dy = 0.926 |
|
||||||||||||||||||||||||
|
⌡ |
⌡0 |
|
|
|
|
|
|
|
⌡ |
⌡4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⌠2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
⌠ |
1 |
|
|
|
|
6−2 y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
⌠ |
|
|
|
|
|
1 |
|
|
|
|
|
|
⌠ |
|
|
|
|
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|||||||||||||||||||||
Dx:= |
|
|
|
|
x |
9 dx dy |
+ |
|
|
|
|
x |
|
9 dx dy − 2.296 = 1.914 |
|||||||||||||||||||||||
⌡ ⌡0 |
|
|
|
|
|
|
|
|
|
|
|
⌡ ⌡4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
⌠2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
⌠1 |
|
|
|
|
|
(6−2 y) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
⌠ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
⌠ |
|
|
|
|
|
1 |
2 |
|
||||||||||
Dy := |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
= 0.346 |
|||||||||||||||||||||
|
|
y |
|
|
|
|
9 dx dy + |
|
|
|
|
|
|
|
|
|
9 dx dy − 0.926 |
||||||||||||||||||||
|
|
|
|
|
|
⌡0 |
|
|
|
|
|
|
|
|
|
|
|
|
⌡4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
⌡0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⌡0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⌠ |
2 |
|
|
4 |
|
|
|
|
|
|
|
⌠1 |
|
|
(6−2 y) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
⌠ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
⌠ |
|
|
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Kxy := |
|
y |
|
|
9 x dx dy + |
|
|
|
|
y |
|
|
|
|
|
|
|
9 |
x dx dy − mX mY = −0.182 |
||||||||||||||||||
|
|
⌡ ⌡0 |
|
|
|
|
|
|
|
|
⌡ ⌡4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Rxy:= |
|
Kxy |
|
|
|
= −0.223 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Dx Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: коэффициент корреляции равен -0,223, что предполагает наличие обратной связи между величинами.
ЗАДАЧА 9.
Одномерная выборка №138:
5.622.43 4.81 5.70 3.68 3.76 2.45 6.21 3.75 4.05 5.98 0.96 1.42 2.69 0.72
5.755.38 3.41 0.33 4.37 5.59 2.95 6.58 2.69 2.05 2.51 3.91 2.86 5.60 3.31 5.53
6.642.20 1.84 6.16 2.22 3.94 1.61 4.87 1.22 5.35 1.61 2.02 5.14 4.41 1.04 6.51
3.851.08 3.36 6.49 6.04 5.67 3.83 1.40 5.32 5.95 5.48 6.18 2.55 6.53 5.33 5.14
4.311.46 5.60 3.97 4.14 3.56 1.51 4.33 6.47 1.02 3.49 0.66 5.37 0.54 3.42 2.74
1.055.03 4.25 4.64 1.80 3.51 6.47 4.35 6.46 6.83 2.45 4.62 3.17 1.79 5.59 4.93
2.113.89 5.70 2.87 4.54
По выборке одномерной случайной величины,:
- получить вариационный ряд; - построить на масштабно-координатной бумаге формата А4 график
эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом; - построить гистограмму равновероятностным способом;
- вычислить точечные оценки математического ожидания и диспер-
сии;
- вычислить интервальные оценки математического ожидания и дис-
персии (γ = 0,95); - выдвинуть гипотезу о законе распределения случайной величины и
проверить ее при помощи критерия согласия χ2 и критерия Колмогорова (α = 0,05). График гипотетической функции распределения F0(x) построить совместно с графиком F*(x) в той же системе координат и на том же листе.
Решение:
1)получим вариационный ряд:
0.330.54 0.66 0.72 0.96 1.02 1.04 1.05 1.08 1.22 1.40 1.42 1.46 1.51 1.61 1.61
1.791.80 1.84 2.02 2.05 2.11 2.20 2.22 2.43 2.45 2.45 2.51 2.55 2.69 2.69 2.74
2.862.87 2.95 3.17 3.31 3.36 3.41 3.42 3.49 3.51 3.56 3.68 3.75 3.76 3.83 3.85
3.893.91 3.94 3.97 4.05 4.14 4.25 4.31 4.33 4.35 4.37 4.41 4.54 4.62 4.64 4.81
4.874.93 5.03 5.14 5.14 5.32 5.33 5.35 5.37 5.38 5.48 5.53 5.59 5.59 5.60 5.60
5.625.67 5.70 5.70 5.75 5.95 5.98 6.04 6.16 6.18 6.21 6.46 6.47 6.47 6.49 6.51
6.536.58 6.64 6.83
Х |
0.33 |
0.54 |
0.66 |
0.72 |
0.96 |
1.02 |
1.04 |
1.05 |
1.08 |
1.22 |
1.40 |
М |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Х |
1.42 |
1.46 |
1.51 |
1.61 |
1.79 |
1.80 |
1.84 |
2.02 |
2.05 |
2.11 |
2.20 |
М |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Х |
2.22 |
2.43 |
2.45 |
2.51 |
2.55 |
2.69 |
2.74 |
2.86 |
2.87 |
2.95 |
3.17 |
М |
1 |
1 |
2 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
Х |
3.31 |
3.36 |
3.41 |
3.42 |
3.49 |
3.51 |
3.56 |
3.68 |
3.75 |
3.76 |
3.83 |
М |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Х |
3.85 |
3.89 |
3.91 |
3.94 |
3.97 |
4.05 |
4.14 |
4.25 |
4.31 |
4.33 |
4.35 |
М |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Х |
4.37 |
4.41 |
4.54 |
4.62 |
4.64 |
4.81 |
4.87 |
4.93 |
5.03 |
5.14 |
5.32 |
М |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
Х |
5.33 |
5.35 |
5.37 |
5.38 |
5.48 |
5.53 |
5.59 |
5.60 |
5.62 |
5.67 |
5.70 |
М |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
Х |
5.75 |
5.95 |
5.98 |
6.04 |
6.16 |
6.18 |
6.21 |
6.46 |
6.47 |
6.49 |
6.51 |
М |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
1 |
Х |
6.53 |
6.58 |
6.64 |
6.83 |
|
|
|
|
|
|
|
М |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
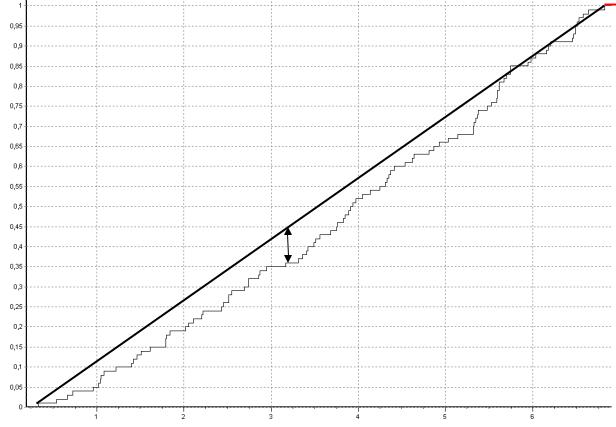
Построим график эмпирической и гипотетической функции распределения:
F*(x)
F0(x)
