ТВиМС вар 17
.doc
1.17 Наудачу взяты
два положительных числа x
и y,
причем x≤5,
y≤2.
Найти вероятность того, что
и
Решение
Количество возможных вариантов выбрать два положительных числа:
Условию
не удовлетворяют следующие комбинации
x
и y:
x=5 y=1;
x=5 y=2;
Условию
удовлетворяют все комбинации.
Тогда, по классической формуле вероятности:
Искомая вероятность
Ответ: 0,8
2.17 Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводи к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1,2,3,4 соответственно равны р1=0,1; р2=0,2; р3=0,3; р4=0,4. Найти вероятность того, что сигнал пройдет со входа на выход.
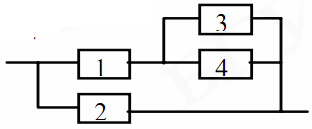
Решение
Найдем вероятность отказа элементов 3,4:
Найдем вероятность отказа элементов 1 и 3,4:
Вероятность одновременного отказа блоков 2 и 1,3,4:
Вероятность безотказной работы блоков 2 и 1,3,4:
Ответ: 0,9584
3.17 Прибор состоит из трех блоков. Исправность каждого блока необходима для функционирования устройства. Отказы блоков независимы. Вероятности безотказной работы блоков соответственно равны 0,6; 0,7; 0,8. В результате испытаний прибор вышел из строя. Определить вероятность того, что отказал один блок.
Решение:
С рассматриваемым событием А={Прибор вышел из строя} связано три гипотезы: Н1={Из строя вышел один блок}, Н2={Из строя вышло два блока}, Н3={Из строя вышло три блока}.
Определим вероятности этих гипотез:
Возможных сочетаний выхода из строя блоков – 7:
- отказал 1 или 2 или 3 блок;
- отказали 1 и 2, или 2 и 3, или 1 и 3.
- отказали все три блока.
Определим условные вероятности события А
По формуле Байеса получим:
Ответ:0,681
4.17 Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что в мишени будет одно или два попадания.
Решение:
Вероятность одного попадания 0,4.
Воспользуемся формулой Бернулли и определим вероятности попасть 1 и 2 раза:
Так как события несовместны
Ответ: 0,4976.
5.17 Дискретная случайная величина Х может принимать одно из пяти фиксированных значений х1=-2, х2=0, х3=2, х4=4, х5=9 с вероятностями р1=0,3, р2=0,2, р3=0,1, р4=0,1, р5=0,3 соответственно. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
Решение
-
xi
-2
0
2
4
9
pi
0,3
0,2
0,1
0,1
0,3
Математическое ожидание
Дисперсия
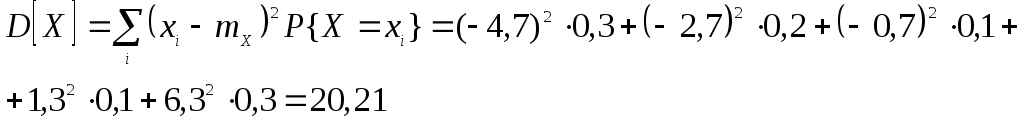
Рассчитаем значения
функции распределения для фиксированных
значений
,
взятых из ряда распределения:
1.
2.
3.
4.
5.
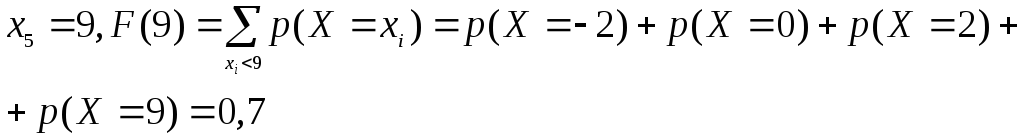
6.17 Случайная величина Х задана плотностью вероятности
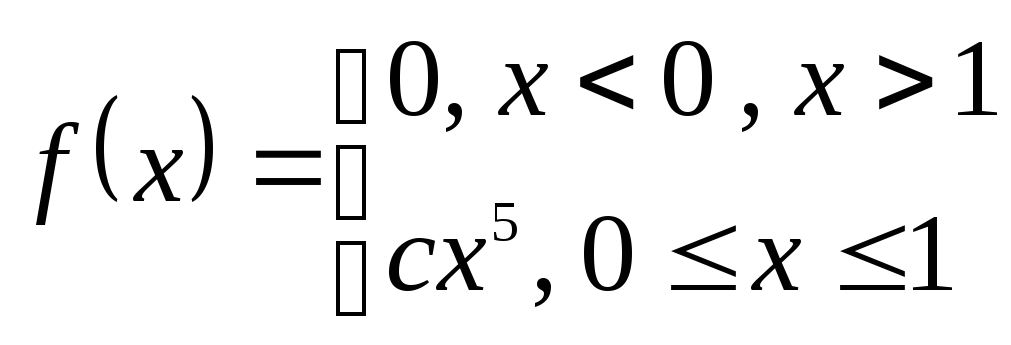
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал [0,5; 0,7]
Решение
Вычислим значение константы С из условия нормировки:
с=6
Определим функцию распределения F(x):
для x<0:
для
для
Окончательно:
Вычислим вероятность
:
Вычислим математическое ожидание:
Вычислим дисперсию:
7.17 Случайная
величина Х распределена равномерно на
интервале
[π/6,π/3]. Построить график
случайной величины
и определить плотность вероятности
g(y),
g(y0),
y0=0,5.
Решение:
Так как Х равномерно распределена в интервале [π/6,π/3], то ее плотность вероятности равна
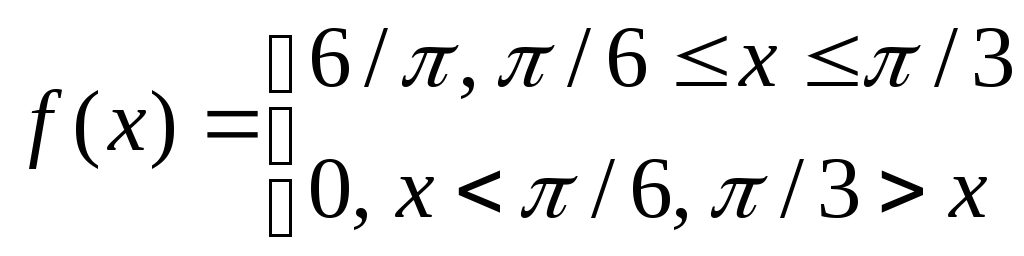
Построим график
величины
для x
в интервале [π/6,π/3].
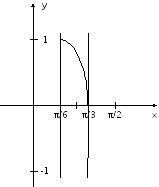
Выделяем интервалы:
[0,1] k=1
На интервалах
обратная функция не существует
.
В интервале [0,1)
одна обратная функция
,
тогда
Таким образом, плотность вероятности величины Y равна
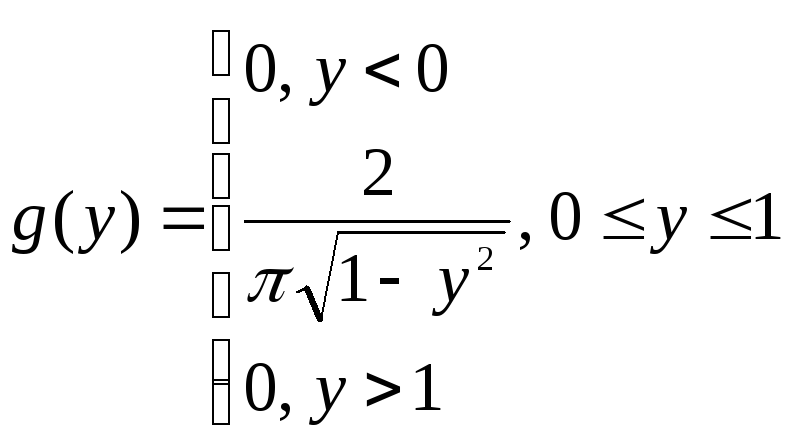
8.17 Двухмерный случайный вектор (X, Y) равномерно распределен внутри области В. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области В:
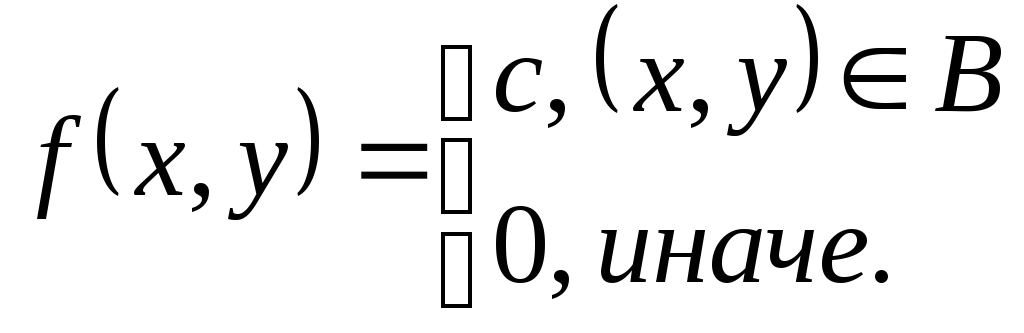
Вычислить коэффициент корреляции между величинами X и Y.
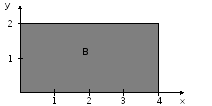
Решение
Запишем в аналитической форме совместную плотность вероятности
Определим с, используя условие нормировки:
Найдем математическое ожидание и дисперсию величины Х
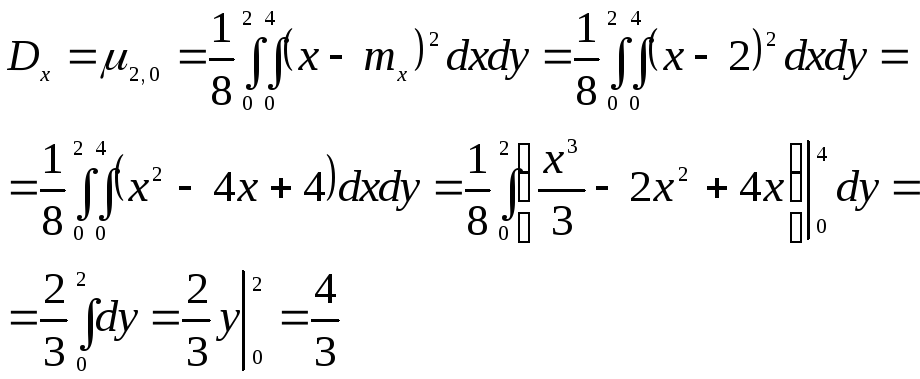
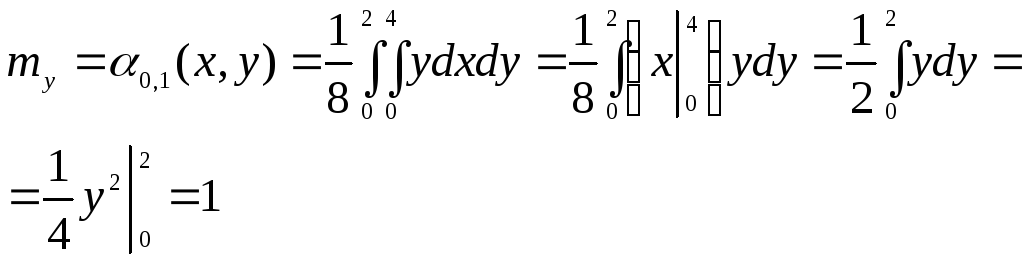
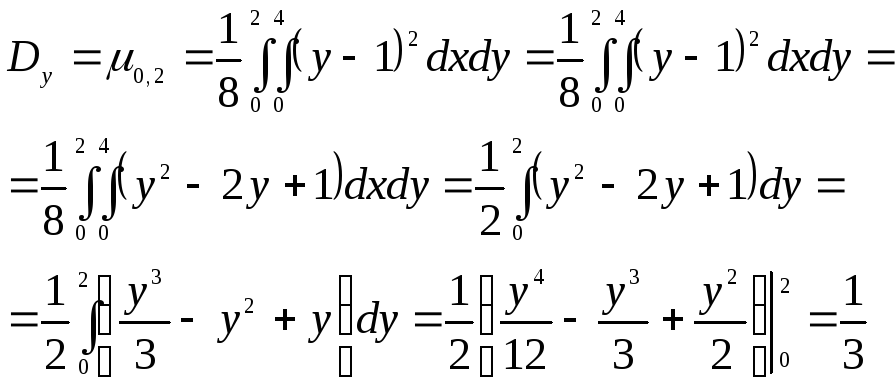
Определим корреляционный момент Kxy:
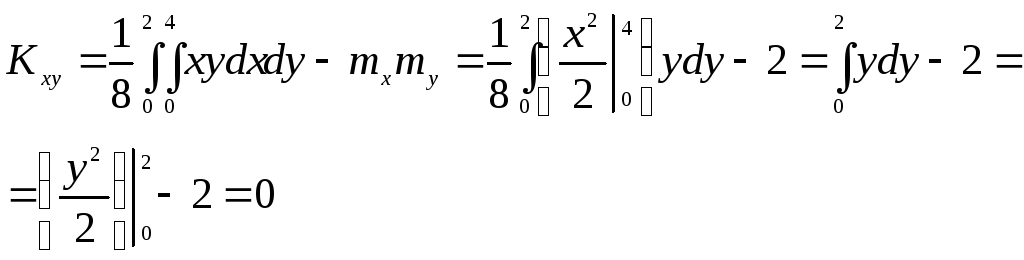
Коэффициент корреляции величин X и Y равен
9.25 По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить оценки математического ожидания и дисперсии;
- выдвинуть гипотезу
о законе распределения случайной
величины и проверить ее при помощи
критерия согласия
и критерия Колмогорова (α=0,05).
Решение
Вариационный ряд
-3,39 -3,39 -3,38 -3,35 -3,33 -3,15 -3,10 -3,07 -3,06 -2,91 -2,90 -2,84 -2,64 - 2,54 -2,53 -2,53 -2,22 -2,18 -2,03 -1,98 -1,92 -1,88 -1,86 -1,81 -1,78 -1,68 -1,66 -1,50 -1,41 -1,32 -1,19 -1,09 -1,00 -0,73 -0,71 -0,67 -0,64 -0,49 -0,28 -0,21 -0,05 0,08 0,12 0,14 0,14 0,31 0,32 0,44 0,49 0,58 0,62 0,63 0,63 0,64 0,69 0,69 0,71 0,73 0,79 0,90 0,94 0,97 0,97 1,00 1,05 1,05 1,21 1,22 1,28 1,34 1,64 1,83 1,86 1,88 1,94 1,95 2,01 2,13 2,16 2,17 2,24 2,28 2,30 2,30 2,31 2,38 2,47 2,54 2,58 2,66 2,66 2,77 2,82 2,89 2,94 3,03 3,27 3,54 3,73 3,77
С F*(x)
x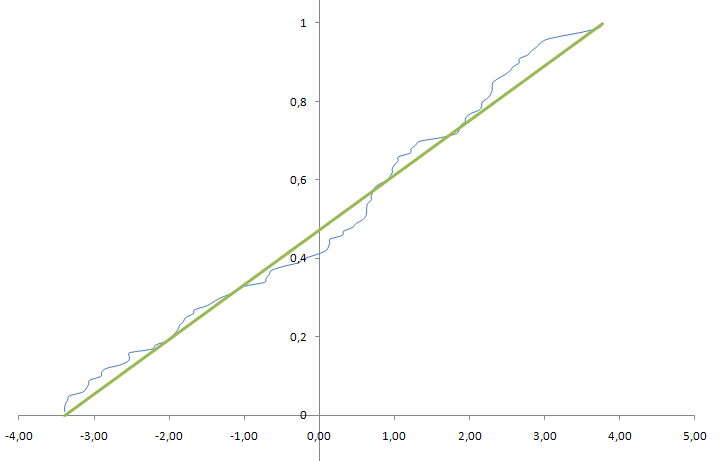
Строим гистограмму равноинтервальным способом. Для этого определим необходимое количество интервалов
-
j
Aj
Bj
hj
vj
p*j
f*j
1
-3,39
-2,674
0,716
12
0,12
0,1676
2
-2,674
-1,958
0,716
8
0,08
0,1117
3
-1,958
-1,242
0,716
10
0,1
0,1397
4
-1,242
-0,526
0,716
7
0,07
0,0978
5
-0,526
0,19
0,716
8
0,08
0,1117
6
0,19
0,906
0,716
15
0,15
0,2095
7
0,906
1,622
0,716
10
0,1
0,1397
8
1,622
2,338
0,716
15
0,15
0,2095
9
2,338
3,054
0,716
11
0,11
0,1536
10
3,054
3,77
0,716
4
0,04
0,0559
;
Равноинтервальная гистограмма имеет вид:
f*(x) x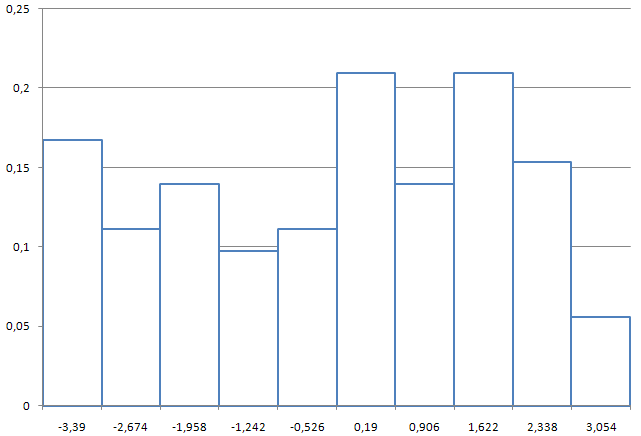
Cтроим гистограмму равновероятностным способом
-
j
Aj
Bj
hj
vj
p*j
f*j
1
-3,39
-2,905
0,485
10
0,1
0,2062
2
-2,905
-1,95
0,955
10
0,1
0,1047
3
-1,95
-1,255
0,695
10
0,1
0,1439
4
-1,255
-0,13
1,125
10
0,1
0,0889
5
-0,13
0,6
0,73
10
0,1
0,137
6
0,6
0,92
0,32
10
0,1
0,3125
7
0,92
1,49
0,57
10
0,1
0,1754
8
1,49
2,205
0,715
10
0,1
0,1399
9
2,205
2,66
0,455
10
0,1
0,2198
10
2,66
3,77
1,11
10
0,1
0,0901
,
,
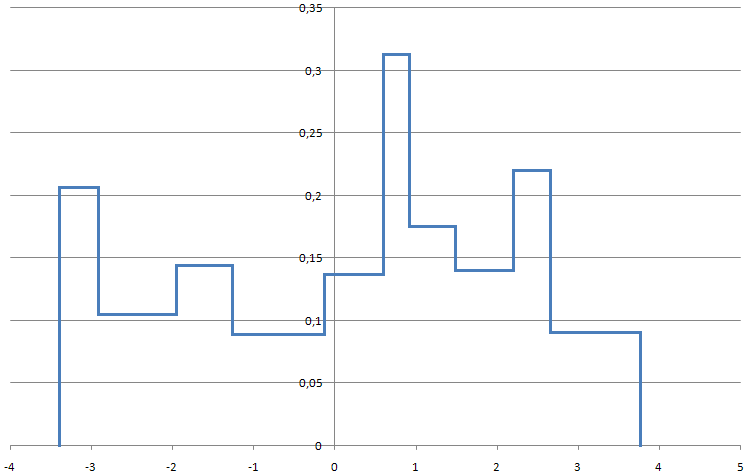
Вычисляем точечную оценку математического ожидания
Вычислим точечную оценку дисперсии
Построим доверительный
интервал для математического ожидания
с надежностью
.
;
;
Построим доверительный
интервал для дисперсии с надежностью
По виду графика эмпирической функции распределения и гистограмм выдвигаем двухальтернативную гипотезу о законе распределения случайной величины:
Н0 – величина Х распределена по равномерному закону
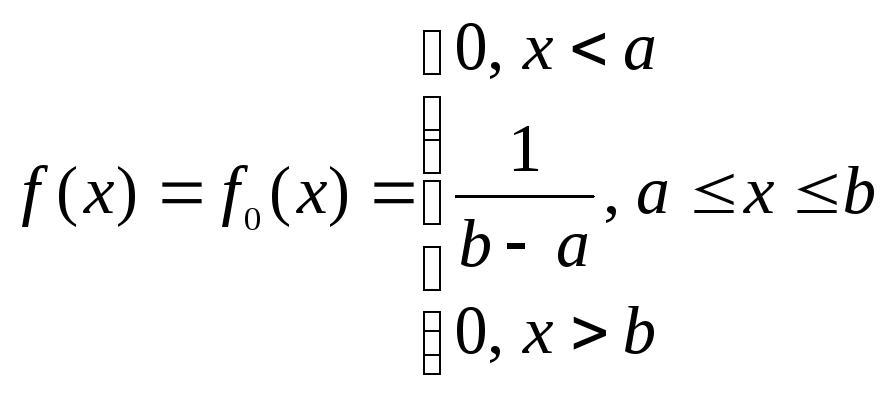
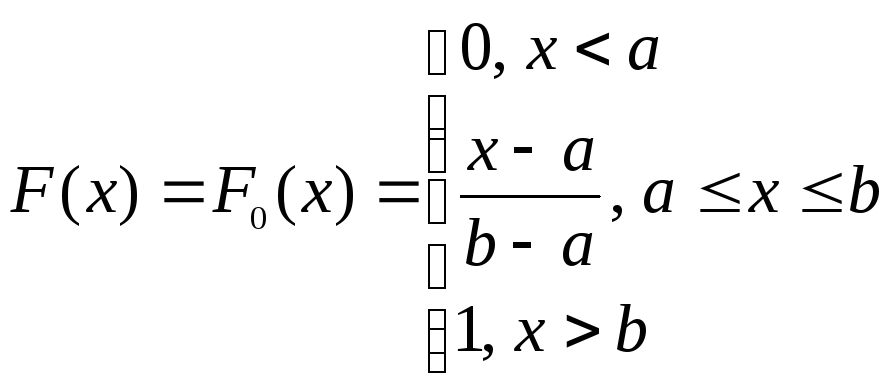
Н1 – величина Х не распределена по равномерному закону
, 
Определим оценки неизвестных параметров a и b
,
Получаем полностью определенную гипотетическую функцию распределения:
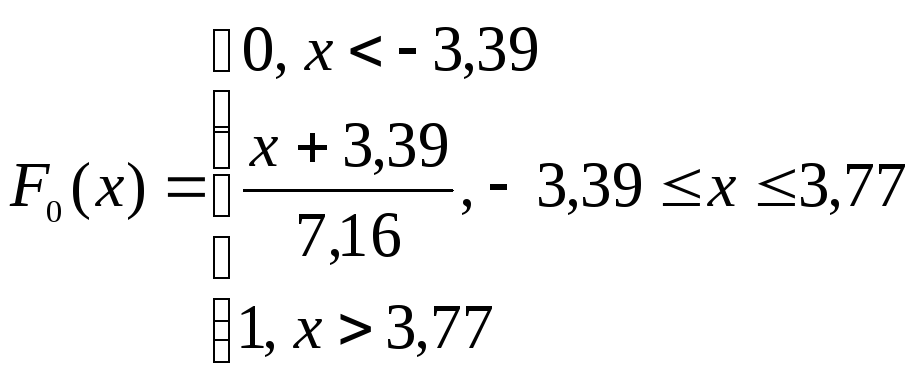
Проверим гипотезу
о равномерном законе с помощью критерия
.
Вычислим значение
критерия
на основе равноинтервального
статистического ряда
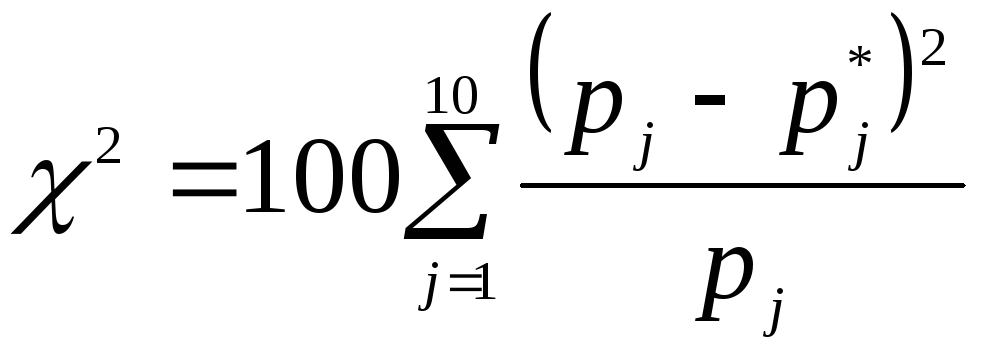
Теоретические вероятности pi попадания в интервалы равноинтервального статистического ряда равномерной случайной величины
-
j
Aj
Bj
F0(Aj)
F0(Bj)
pj
p*j
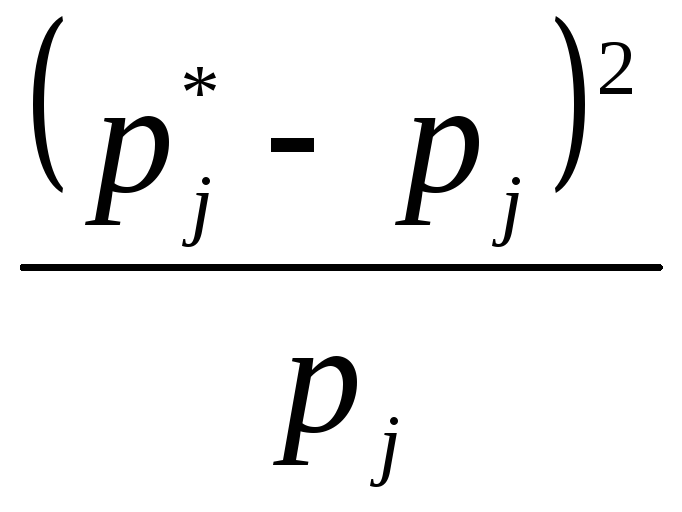
1
-3,39
-2,674
0
0,1
0,1
0,12
0,004
2
-2,674
-1,958
0,1
0,2
0,1
0,08
0,004
3
-1,958
-1,242
0,2
0,3
0,1
0,1
0
4
-1,242
-0,526
0,3
0,4
0,1
0,07
0,009
5
-0,526
0,19
0,4
0,5
0,1
0,08
0,004
6
0,19
0,906
0,5
0,6
0,1
0,15
0,025
7
0,906
1,622
0,6
0,7
0,1
0,1
0
8
1,622
2,338
0,7
0,8
0,1
0,15
0,025
9
2,338
3,054
0,8
0,9
0,1
0,11
0,001
10
3,054
3,77
0,9
1
0,1
0,04
0,036
Сумма
1
1
0,108
Проверяем выполнение контрольного соотношения для pj
Получаем
Вычисляем число степеней свободы
По заданному уровню
значимости
из таблицы распределения
выбираем критическое значение
Так как
то гипотеза Н0
о равномерном законе распределения
принимается (не основания ее отклонить).