
- •Представление задач в пространстве состояний
- •Алгоритмы перебора в ширину и глубину в пространстве состояний
- •Алгоритм равных цен
- •Изменения при переборе в произвольных графах.
- •Алгоритм упорядочения поиска в пространстве состояний.
- •Оптимальный алгоритм эвристического поиска а*
- •Критерии качества работы эвристических алгоритмов.
- •Метод сведения задач к подзадачам
- •Основные методы поиска в "и–или" деревьях Перебор в ширину в деревьях и – или.
- •Построение потенциального дерева решений 0. Эвристический поиск в деревьях и-или Стоимость деревьев типа и-или.
- •Алгоритм упорядочения перебора при сведении задач к подзадачам
- •Особенности поиска решений в игровых задачах
- •" " Процедура в игровых задачах
- •Системы искусственного интеллекта на основе решателей задач
- •Системы понимания естественного языка (ея).Морфологический анализ.
- •Синтаксический анализ предложений, семантический анализ естественного языка.
Основные методы поиска в "и–или" деревьях Перебор в ширину в деревьях и – или.
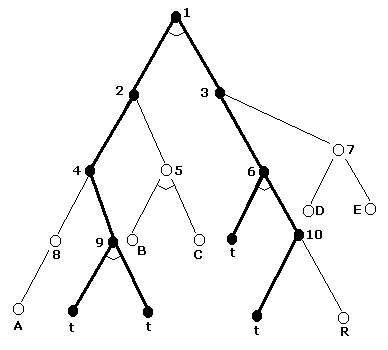
Рассмотрим алгоритм поиска в ширину в деревьях И-ИЛИ, а потом обобщим его на произвольный граф.
1) Начальную вершину помещаем в список OPEN.
2) Взять первую вершину из OPEN и поместить её в CLOSED. Обозначить её через n.
3) Раскрыть вершину n и поместить пораженные вершины в конец списка OPEN. Провести указатели к n. Если порожденных вершин нет, то пометить n, как неразрешимую и перейти к п.4., иначе к п.8.
4) Применить к дереву процедуру на неразрешимость.
5) Если начальная вершина неразрешима, то решения нет. Выход
6) Изъять из OPEN все вершины, имеющие неразрешимые предшествующие вершины.
7) Перейти к п.2.
8) Если все порожденные вершины заключительные, то пометить их как разрешимые и перейти к п.2. Заключительные вершины - это разрешимые и концевые.
9) Применить к дереву разметку на разрешимость.
10) Если начальная вершина разрешима, то выдать решение используя указатели. Выход.
11) Изъять из OPEN все разрешимые вершины и разрешимые предшествующие вершины.
12) Перейти к п.2.
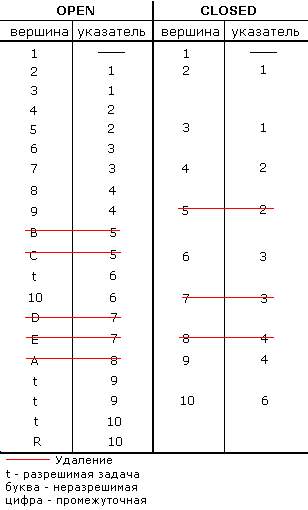
Построение потенциального дерева решений 0. Эвристический поиск в деревьях и-или Стоимость деревьев типа и-или.
Для эвристического поиска в деревьях И-ИЛИ вводится понятие стоимости такого дерева. Дерево минимальной стоимости, содержащее дерево решений будем называть оптимальным деревом решений.
Через
h(S) обозначим минимальную стоимость
дерева решений с корнем в начальной
вершине S. Через h(n) обозначим минимальную
стоимость поддерева с корнем в вершине
n.
![]() -
стоимость дуги между вершинами
и
-
стоимость дуги между вершинами
и
![]() .
.
Стоимость дерева определяется рекурсивно. Стоимость заключительной вершины равно нулю.1) h(n)=0 - заключительная
2)
Для вершин типа ИЛИ.
![]() 3)
Для вершин типа И.
3)
Для вершин типа И.
![]()
![]() .
.
Введём
оценочную функцию для каждой вершины
.
Для неё справедливы все 3 соотношения,
что и для h(n).
![]() определяется
из некоторой эвристической информации.
определяется
из некоторой эвристической информации.
Согласно
оценкам
на
каждом шаге перебора можно посчитать
верхнюю часть минимального дерева
решений. Эту часть будем называть
потенциальным деревом решений и
обозначать
0.
Потенциальное дерево решений можно
определить следующим образом:1) Начальная
вершина входит в
0.2)
Если у вершины, принадлежащей
0
есть порожденные ИЛИ вершины, то в входит
та из них, для которой минимально значение
![]() .3)
Если у вершины n, принадлежащей
0
есть порождённые И вершины, то все они
входят в
0.
.3)
Если у вершины n, принадлежащей
0
есть порождённые И вершины, то все они
входят в
0.
ПРИМЕР:
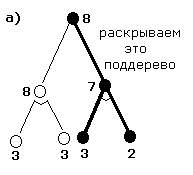
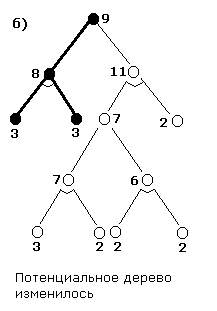
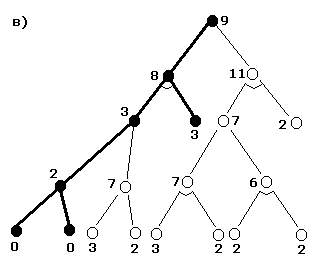
Будем
предполагать, что известно правило, по
которому можно определить, какую из
концевых вершин дерева
0
нужно раскрывать следующей. Цена дуг в
данном примере равно единице. Известны
оценочные функции для концевых вершин.
Изобразим потенциальные деревья решений.
Для деревьев И-ИЛИ справедлива следующая
теорема.ТЕОРЕМА: Если значение
![]() h(n)
для любой раскрытой вершины n в ходе
поиска и стоимости всех дуг не превосходят
некоторую величину
<0, то алгоритм упорядоченного перебора
в вершинах И-ИЛИ допустим, т.е. обеспечивает
поиск оптимального решения. При этом
оптимальность алгоритма не доказана
(число шагов не минимально).
h(n)
для любой раскрытой вершины n в ходе
поиска и стоимости всех дуг не превосходят
некоторую величину
<0, то алгоритм упорядоченного перебора
в вершинах И-ИЛИ допустим, т.е. обеспечивает
поиск оптимального решения. При этом
оптимальность алгоритма не доказана
(число шагов не минимально).
