Алгоритм равных цен

Это модификация перебора в ширину, которая учитывает стоимость дуг. В этом случаи для каждой вершины, кроме указателя на родительскую вершину нужно запоминать и стоимость пути. Для дерева это минимальный путь. Особенностью метода является то, что вершины раскрываются в порядке возрастания стоимостей g(n).

1. Помещаем начальную вершину в список OPEN. Полагаем

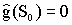
2. Если OPEN пуст то решений нет.

3. Взять из OPEN ту вершину, для которой =min(). В случаи равенства значений - любую из них отдавая предпочтение целевой. Перенесём эту вершину в CLOSED и обозначим n как текущую вершину.

4. Если n - целевая вершина, то построить решение используя указатели.

5. Раскрыть вершину n, построить порождённые вершины, если таких нет то переходим к п2. 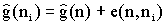. Поместить эти вершины в список OPEN вместе с ценами 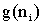и указателями на n

6. Перейти к п2.

Если целевая вершина описана явно то процесс перебора можно построить в обратном порядке. Для этого нужно обратить оператор Г.

Алгоритм поиска в глубину

Раскрываем в первую очередь вершины, которые порождены последней. Глубина дерева определяется рекурсивно. Глубина корня=0. Глубина последующей вершины равна глубине родительской + 1. При переборе в глубину наибольшую глубину имеет вершина раскрытая последней в данный момент.

АЛГОРИТМ:

1. Поместить начальные вершины в OPEN.

2. Если OPEN пуст, то нет решений

3. Взять последнюю вершину из OPEN и переместить в CLOSED и обозначить через n

4. Если глубина n= граничной то перейти к п2.

5. Раскрыть вершину n, поместив все порожденные в конец списка OPEN и построить указатели к n.

6. Если одна из вершин целевая, то выдать решение, используя указатели. Иначе перейти к п2.

Для поиска в глубину часто используют стек, тогда не нужны указатели.

Изменения при переборе в произвольных графах.

В том случае, когда пространство поиска представляет собой не дерево, а связный граф, алгоритмы поиска в ширину и в глубину нуждаются в модификации. В данном случае, в процессе поиска м.б. найден более короткий путь от множества начальных вершин до текущей вершины.

Для поиска в произвольном графе без учёта стоимостей нужно только проверить есть ли данная вершина в списках OPEN или CLOSED и если она там есть, то второй раз её не вносить, а только изменить указатель.

В алгоритме равных цен:Если построенная вершина уже есть в списке OPEN, то её вносить в список не следует, но необходимо изменить величину и указатель в том случае, когда найден более короткий путь. Если вершина помещена в CLOSED, то ничего изменять не нужно, поскольку в этом случаи наименьшее.

В поиске в глубину:Необходимо пересчитывать глубину при раскрытии той же самой вершины.

В произвольном графе множество вершин и указателей на каждом шаге перебора образуют дерево.

3. Алгоритм упорядочения поиска в пространстве состояний.

Алгоритм упорядоченного перебора А:

1. Поместить начальные вершины в список OPEN и вычислить значение .

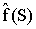2. Если список OPEN пусть, значит решений нет.

3. Взять из OPEN ту вершину для которой - минимально, перенести её в CLOSED. Дать этой вершине имя n. В случаи равенства значений -, выбрать любую, отдавая предпочтение целевой.

4. Если n - целевая вершина, то выход с указанием решения по средствам указателей.

5. Раскрыть вершину n. Для порожденных вершин посчитать 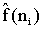. Если порожденных вершин нет то перейти к п2.

6. Связать с теми вершинами n_i- которых нет в списках OPEN и CLOSED посчитанные значения и поместить их в список OPEN. Провести указатели к n.

7. Те порожденные вершины, которые есть в OPEN и CLOSED связать со значениями 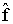, если эти значения меньше, чем вычисленные раньше. Поместить их в OPEN и связать указателями к вершине n.

8. П ерейти к пункту 2.

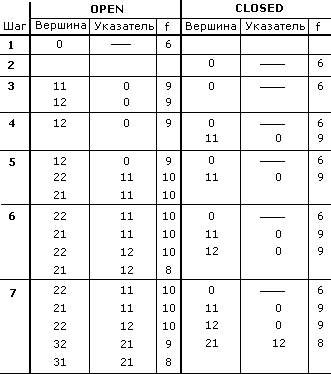
П РИМЕР:

Оптимальный алгоритм перебора

Оптимальным называется алгоритм, который позволяет определить оптимальный путь при минимальном количестве открытых вершин. При этом алгоритм, который гарантирует нахождение оптимального пути будем называть допустимым (не обязательно оптимальным)

Оптимальным будем называть любое решение минимальной стоимости, связывающее начальную и конечную вершины.

В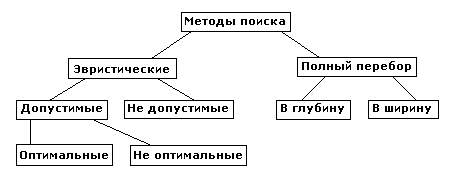 формуле для текущего значения целевой функции первое слагаемое определяется по ходу решения. Второе слагаемое определяется исходя из эвристической информации

Харт, Нильсон и Рафаэль определили условие при котором алгоритм упорядоченного перебора А становится оптимальным становится оптимальным алгоритмом А^*. Это условие сформулировано в следующей теореме:

ТЕОРЕМА:

Если для всех вершин n выполняется условие

где -эвристическое значение n - действительное. И стоимости всех дуг превосходят некоторое число  >0, то алгоритм А будет допустимым.

Выбрав в качестве найбольшей из нижних границ прейдем к тому, что раскрывается наименьшее число вершин, при допустимости алгоритма, т.е. А^* становится оптимальным, если в качестве выбирается

ЗАМЕЧАНИЕ:

Часто эвристическая сила алгоритма может быть повышена если n не является нижней границей, но при этом не сохраняется допустимость алгоритма.