Модуль 1

Практичне заняття 4

Числові функції.

Основні теоретичні відомості

Функція називається числовою, якщо вона визначена при всіх натуральних значеннях аргументу .

Через позначають числову функцію, значення якої для будь-якого натурального числа дорівнює числу всіх його натуральних дільників.

Через позначають числову функцію, значення якої для будь-якого натурального числа дорівнює сумі всіх його натуральних дільників.

Через позначають числову функцію, значення якої для будь-якого натурального числа дорівнює кількості натуральних (цілих невід’ємних ) чисел, взаємно простих з , які не перевищують . Функцію називають функцією Ейлера.

Через позначають числову функцію, значення якої для будь-якого дійсного числа дорівнює найбільшому цілому числу, яке не перевищує . Функцію називають цілою частиною від .

Через позначають числову функцію, значення якої для будь-якого дійсного числа дорівнює різниці . Функція називається дробовою частиною від .

Числова функція називається мультиплікативною, якщо для кожного функція і для будь-яких взаємно простих натуральних чисел і виконується рівність .

Мультиплікативні функції мають такі властивості:

;

1. Добуток мультиплікативних функцій є мультиплікативна функція;

2. Якщо , , , попарно взаємно прості, то .

3. Числові функції , , мультиплікативні. Якщо - канонічний розклад натурального числа , то

, (1)

, (2)

, (3)

Зрозуміло, що , згідно з означенням цих функцій.

Сума значень функції Ейлера для всіх дільників числа дорівнює :

(формула Гаусса) (4)

Зауваження.

1. . В усіх інших випадках може бути тільки парним числом4

2. , якщо ;

3. ;

4. , якщо .

Якщо , то .

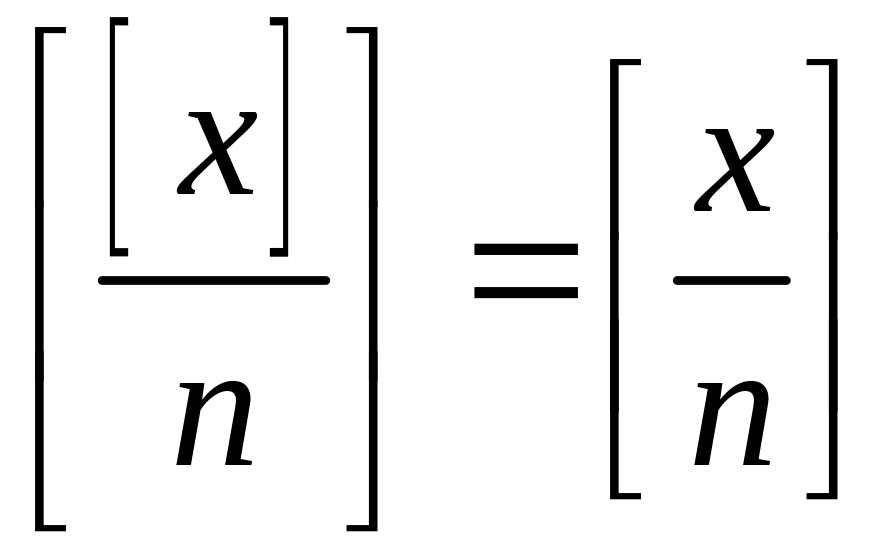Показник простого числа , яке входить до канонічного розкладу натурального числа обчислюється за формулою

, де (5)

- прості числа.

Кількість цілих додатних чисел, які не перевищують і не діляться на жодне з простих чисел , обчислюється за формулою:

(6)

Властивості цілої та дробової частини числа

виконуються властивості:

1. ;

2. ;

3. Якщо , , то ;

4. ;

5. ;

6. , якщо ;

7. , якщо ;

8. і ;

9. ;

10. Для будь-якої кінцевої кількості доданків

11. Якщо , то .

12. Якщо , то ;

13.

.

14.

.

Приклад 1. Знайти число і суму всіх натуральних дільників числа .

Розв’язання. Знаходимо канонічний розклад числа . . Тоді

,

.

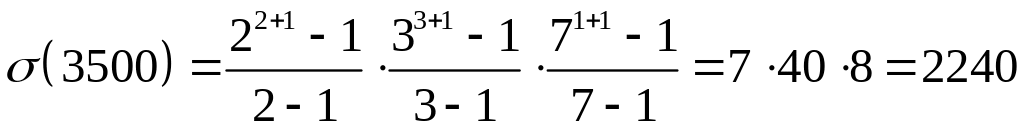Відповідь: , .

Приклад 2. Знайти натуральне число , якщо:

а) має тільки два простих дільники, , ;

б) , , , .

Розв’язання. а) Оскільки , то .

Рівність можлива тільки при і . Тоді .

б) Якщо , то

, ,

, .

Складемо систему рівнянь і розв’яжемо її

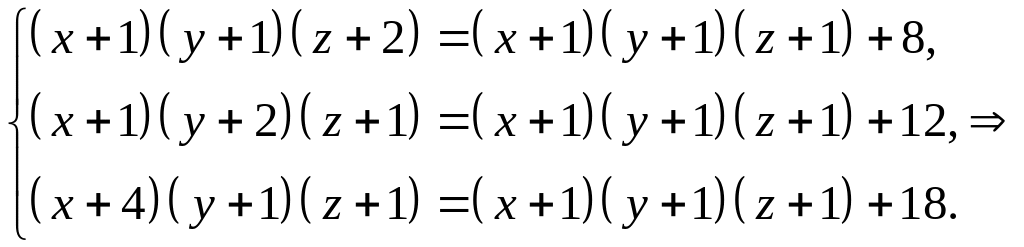
Останні рівності можливі тільки при , , . Тоді .

Відповідь: а) ; б) .

Приклад 3. Нехай – натуральне число. Знайти , якщо і має тільки три простих дільники.

Розв’язання. За умовою , де – прості числа. Тоді , а .

.

Отже, .

Відповідь: .

Приклад 4. Знайти функцію Ейлера для чисел:

а) б)

Розв’язання. а) Знайдемо канонічний розклад числа :

.

Тоді .

б) .

Відповідь: а) ; б) .

Приклад 5. Знайти кількість натуральних чисел, які менші від числа і мають з ним найбільший спільний дільник .

Розв’язання. За умовою , всі значення . Поділимо та на , де всі значення і взаємно прості з . Кількість значень обчислимо за формулою

,

.

Відповідь: Існує чисел менших , які мають з найбільший спільний дільник .

Приклад 6. Розв’язати рівняння .

Розв’язання. Нехай - просте число. Тоді .

, , а - складене число.

Висновок: - складене число.

Нехай , де - прості числа менші . Отже, можуть набувати значень .

Якщо , то ,

якщо , то ,

якщо , то ,

якщо , то ,

якщо , то .

Відповідь: може набувати значень .

Приклад 7. Знайти натуральне число , якщо , де - різні прості числа, і .

Розв’язання. .

Способом підбору знаходимо декілька розв’язків даної задачі. Числа і повинні бути меншими .

1) , ,

2) , ,

3) , ,

4) , ,

5) , .

Відповідь: .

Приклад 8. Розв’язати рівняння .

Розв’язання. .

.

Відповідь: .

Приклад 9. Скількома нулями закінчується число ?

Розв’язання. Відповіддю має бути максимальний степінь числа , на який ділиться число Але . Число входить множником у значно частіше, ніж . Тому розв’язком буде максимальний степінь числа , на який ділиться . Використавши формулу (5), отримаємо, що

Відповідь: Число закінчується -ю нулями.

Приклад 10. Розв’язати рівняння .

Розв’язання. Для знаходження розв’язків рівняння розв’яжемо двосторонню нерівність , яка рівносильна системі нерівностей

.

Відповідь: .

Якщо ж , наприклад, розглянути рівняння , то хоч необхідна умова існування коренів (права частина рівняння ціле число) виконується , проте рівняння коренів не має, бо функція може набувати в області її визначення тільки невід’ємних значень.

Приклад 11. Розв’язати рівняння .

Розв’язання Область визначення , , . Позначимо , . Звідси знайдемо і підставимо його в дане рівняння:

,

.

Матимемо

; ; ;

Множиною розв’язків першої нерівності будуть , які задовольняють умову , а другої нерівності –

, .

Тоді множиною розв’язків системи нерівностей буде

, .

Оскільки - ціле число, то

Тоді

Перевірка.

а)

б)

в)

г)

Відповідь: .

Приклад 12. Розв’язати рівняння .

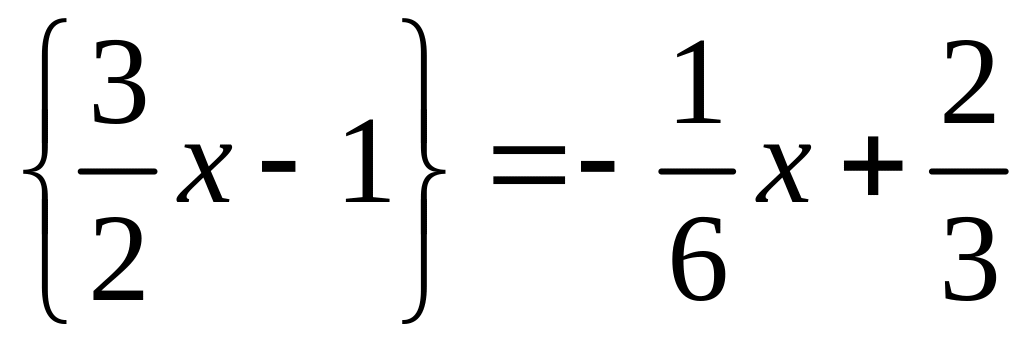Розв’язання. Враховуючи рівність , дістанемо

.

Звідси

,

.

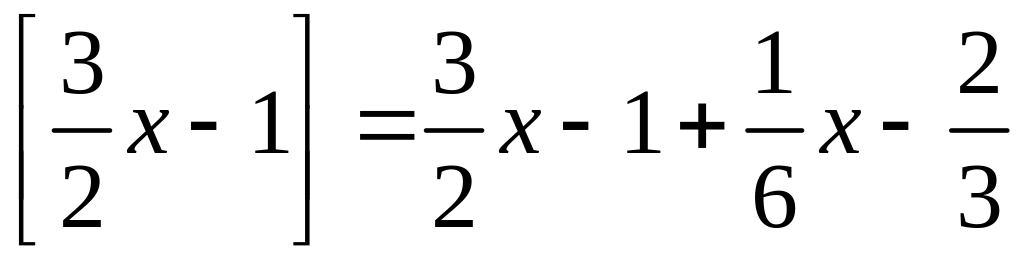Позначимо 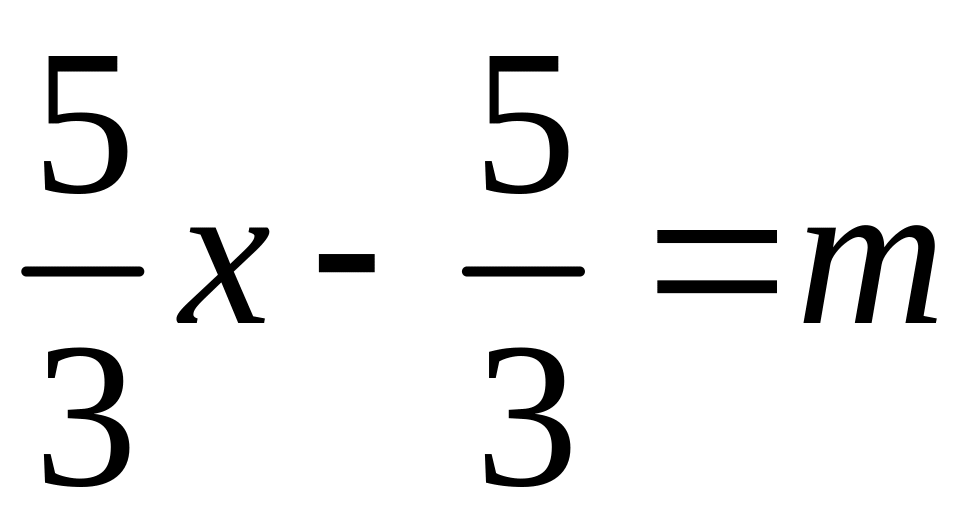, . Виразимо через :

.

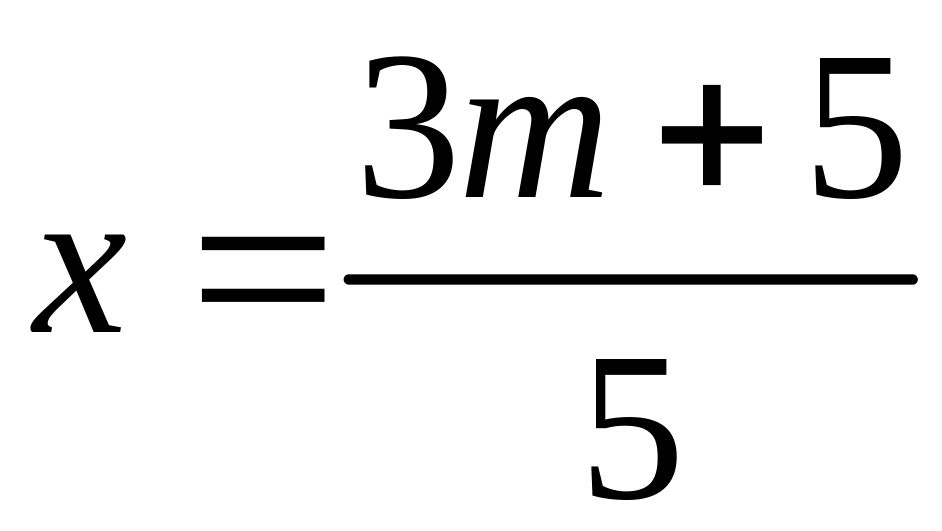Підставимо знайдене значення в останнє рівняння. Матимемо

, .

Тепер повинно задовольняти умову

, ,

.

Цілими розв’язками будуть . Підставляючи по черзі знайдені значення в , дістанемо:

а) , , ;

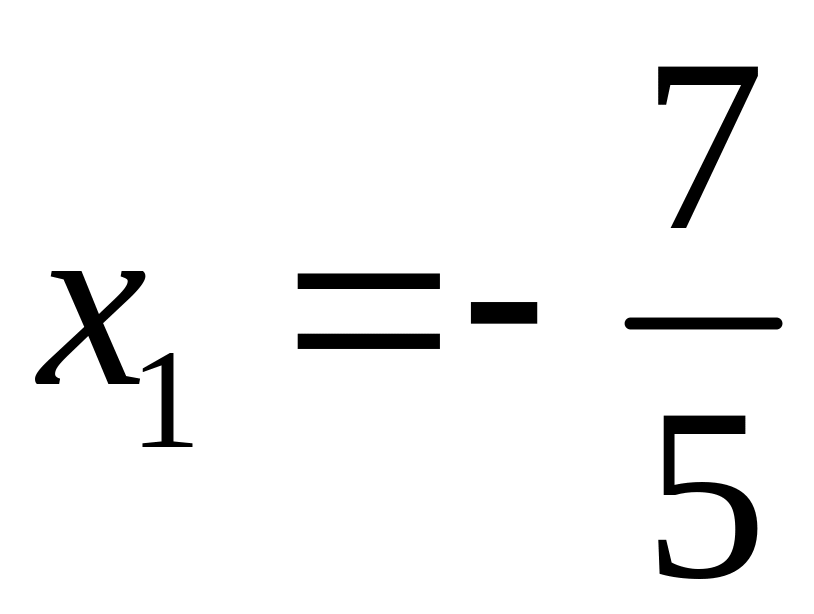б) , , ;

в) , , ;

г) , , ;

д) , , ;

е) , , ;

є) , , ;

ж) , , ;

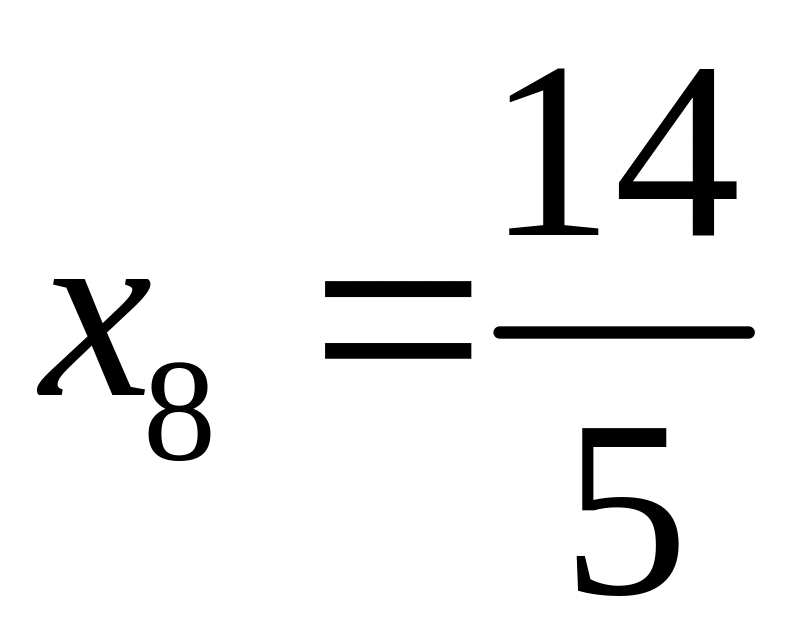з) , , ;

и) , , .

Зауваження. Враховуючи, що функції і лінійні, а значення повторюються через , можна було за першими двома коренями записати решту.

Відповідь: .

Розглянемо побудову графіків функцій, пов'язаних з функціями: ціла частина дійсного числа і дробова частина дійсного числа .