Модуль 3

Лекція 5

Розміщення дійсних коренів многочлена

Розглянемо питання, пов‘язане з розміщенням на дійсній осі коренів рівняння з дійсними коефіцієнтами.

Зробимо зауваження щодо комплексних коренів многочленів. Ці зауваження є наслідками раніше з‘ясованих фактів.

1. Усі корені многочлена лежать усередині круга з центром у точці і радіусом

. (63)

Це випливає з наслідку 1 теореми 21. (Лекція 1 модуль 3).

2. Комплексні корені многочлена з дійсними коефіцієнтами розміщені симетрично відносно дійсної осі.

Далі, переходячи до розгляду дійсних коренів многочленів з дійсними коефіцієнтами, будемо знову позначати змінне буквою , а не .

Теорема 32. Усі дійсні корені рівняння

містяться в інтервалі , де

.

Дійсно, всі комплексні корені лежать у крузі , а тому, якщо серед них є дійсні, то вони повинні потрапити в зазначений інтервал .

Теорему 32 часто називають про межі коренів рівняння. Є немало способів, які дають змогу з більшою точністю встановлювати межі дійсних коренів алгебраїчних рівнянь. Розглянемо один з них, так званий спосіб Ньютона, який дає змогу знайти більш точно межі додатних та від‘ємних коренів многочленів з дійсними коефіцієнтами.

Число , визначене за теоремою 32, дає одночасно верхню межу додатних коренів многочлена і нижню межу його від‘ємних коренів , бо вказує інтервал , в якому лежать усі дійсні корені, якщо вони існують. один з шляхів уточнення меж, між якими слід шукати дійсні корені, полягає в тому, щоб окремо знаходити нижню і верхню межі додатних коренів та нижню і верхню межі від‘ємних коренів даного многочлена, тобто такі чотири числа , що всі додатні корені многочлена лежать в інтервалі , а всі від‘ємні – в інтервалі . Якщо многочлен має корінь нуль, досить розглянути многочлен, утворений з даного діленням на .

Фактично досить знайти спосіб знаходження лише одного з цих чотирьох чисел, наприклад верхньої межі додатних коренів. Знаходження інших трьох меж дійсних коренів рівняння легко звести до знаходження верхньої межі додатних коренів деяких допоміжних рівнянь.

Зробивши в рівнянні заміну змінного , дістанемо рівняння , корені якого зв‘язані з відповідними коренями заданого рівняння співвідношенням . Якщо верхня межа додатних коренів рівняння , тобто , то , звідки видно, що за нижню межу додатних коренів рівняння можна взяти число :

.

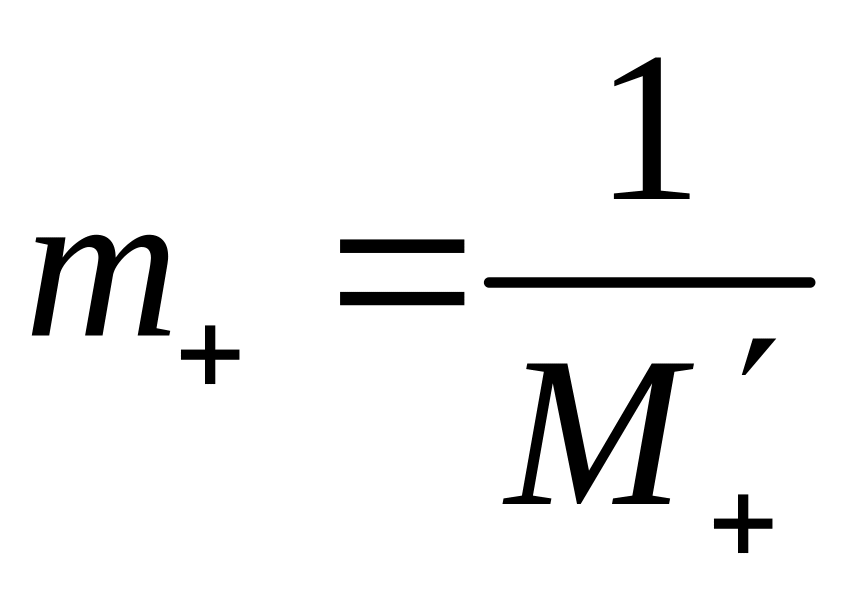Аналогічно, заміна переводить рівняння в рівняння , корені якого зв‘язані з відповідними коренями рівняння рівністю . Якщо всі додатні корені рівняння , то всі від‘ємні корені рівняння . З нерівності видно, що , тобто верхня і нижня межі від‘ємних коренів рівняння виражаються через межі додатних коренів рівняння :

.

Теорема 33 (Ньютона). Число є верхньою межею додатних коренів многочлена , якщо при многочлен має додатне значення, а всі його похідні – невід‘ємні значення.

Доведення. Ураховуючи, що є функція дійсної змінної, для якої справедлива формула Тейлора (відома з курсу аналізу), можемо записати:

,

звідки безпосередньо видно. що при , тобто всі дійсні корені многочлена менші за .

Оскільки знак многочлена і його похідних у точці збігається з знаком відповідних коефіцієнтів розкладу за степенями , на практиці числа зручно підбирати за допомогою схеми Горнера послідовного ділення на . При цьому в більшості випадків немає потреби обчислювати всі коефіцієнти: як тільки в процесі ділення на дістаємо рядок з невід‘ємних чисел, - можна прийняти за верхню межу додатних коренів, бо дальше застосування схеми Горнера ніколи не приведе до від‘ємних коефіцієнтів. Зокрема, якщо заданий многочлен має невід‘ємні коефіцієнти, можна вважати , тобто многочлен не має додатних коренів.

Приклад

Число дійсних коренів

Число дійсних коренів з урахуванням кратності або дорівнює степеню рівняння, або на парне число менше. Будь-яке рівняння непарного степеня з дійсними коефіцієнтами має хоча б один дійсний корінь.

Зрозуміло, що цікаво визначити точне число дійсних коренів.

Обчислюючи значення многочлена в окремих точках, ми можемо знайти, що в деяких точках , він приймає значення різних знаків. Оскільки многочлен – неперервна функція, звідси випливає, що в деякій точці інтервалу він повинен перетворюватися в нуль. (Звісно, це ще не означає, що в інтервалі знаходиться рівно один корінь многочлена ).

Таким способом ми можемо оцінити знизу число дійсних коренів. Однак точне визначення цього числа потребує залучення інших методів.

Наприклад, для многочлена знаходимо: Отже, має корені на кожному з інтервалів Неважко показати, що при а також при Тоді всі дійсні корені многочлена лежать в інтервалі Однак ми не можемо на основі виконаних обчислень стверджувати, що в цьому інтервалі знаходиться лише два корені, тобто, що многочлен має лише два дійсних корені. Це можна було б довести, наприклад, за допомогою теореми Декарта: число додатних коренів многочлена з дійсними коефіцієнтами не перевищує числа змін знака в послідовності його коефіцієнтів.

Існують теореми, наприклад, теорема Штурми, які дозволяють точно визначити число дійсних коренів будь-якого многочлена з дійсними коефіцієнтами.

У багатьох випадках число дійсних коренів рівняння з дійсними коефіцієнтами можна визначити за правилом Декарта. Перш ніж сформулювати це правило, зробимо деякі зауваження.

1. Ми будемо розглядати кількість змін знаків у даній упорядкованій скінченній послідовності дійсних чисел

(64)

розуміючи під цим кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки.

Наприклад, у послідовності є 3 зміни знаків, а в послідовності є 0 змін знаків.

Якщо які-небудь з чисел дорівнюють 0, то при підрахунку числа змін знаків їх до уваги не беруть.

Зауважимо, що коли перше й останнє числа і даної послідовності мають однакові знаки, то кількість змін знаків у послідовності (64) парна; якщо ж і мають протилежні знаки, то кількість змін знаків непарна.

2. Припускатимемо, що розглядуваний многочлен не має кратних коренів, оскільки завжди можна відокремити кратні множники.

Правило Декарта. Число додатних коренів многочлена з дійсними коефіцієнтами

(65)

дорівнює числу змін знаків у послідовності його коефіцієнтів або на парне число менше.

Приклад 1. Для многочлена число змін знаків у послідовності коефіцієнтів дорівнює 4. Отже, за теоремою Декарта він має 4 або 2 додатних дійсних коренів.

Приклад 2. Для лівої частини многочлена число змін знаків у послідовності коефіцієнтів дорівнює 0, тому додатних коренів це рівняння не має.

Приклад 3. Число змін знаків коефіцієнтів у рівнянні дорівнює 1, тому рівняння напевне має один додатний корінь.

Зауваження.

1. Правило Декарта можна застосувати і для оцінки числа від’ємних коренів рівняння з дійсними коефіцієнтами.

Для цього в рівнянні (65) треба зробити заміну змінного Зрозуміло, що число від’ємних коренів даного рівняння дорівнює числу додатних коренів рівняння яке можна оцінити за правилом Декарта.

2. Коли наперед відомо, що всі корені даного рівняння дійсні, то правило Декарта дає точну відповідь на питання про число дійсних коренів, а саме: число додатних коренів дорівнює числу змін знаків у ряді коефіцієнтів многочлена а число від’ємних коренів - числу змін знаків у ряді коефіцієнтів многочлена .

У більшості випадків наперед невідомо, чи всі корені рівняння дійсні. В зв’язку з цим правило Декарта, хоч і зручне з точки зору простоти застосування, не дає повної відповіді на питання про число дійсних коренів рівнянь з дійсними коефіцієнтами та їх розподіл між додатною і від’ємною півосями.

Відокремлення коренів методом Штурма

Далі перейдемо до питання скільки дійсних коренів рівняння з дійсними коефіцієнтами лежить у довільному, наперед заданому інтервалі дійсної осі.

Повну відповідь на це питання дає метод Штурма.

Нехай - деякий многочлен з дійсними коефіцієнтами, Припустимо, що не має кратних коренів.

Знайдемо похідну і побудуємо для та алгоритм, подібний до алгоритму Евкліда; відмінність полягатиме в тому, що всі остачі ми братимемо з протилежними знаками, тобто Позначимо Таким чином, одержимо:

(66)

де так як і взаємно прості (за припущенням, не має кратних коренів) і тому

Послідовність многочленів

(67)

називається рядом функцій Штурма, або просто рядом Штурма.

У методі Штурма нас цікавитимуть не самі функції ряду Штурма або їх значення, а лише знаки числових значень цих функцій. У зв’язку з цим функції ряду (67) можна знаходити з точністю до сталого додатного множника, тобто, виконуючи ділення з остачею, домножати на сталі множники; ці множники обов’язково повинні бути додатні, щоб не змінювались знаки значень многочленів.

Приклад. Знайти ряд Штурма для многочлена

Розв’язання. Знайдемо ряд Штурма для даного многочлена. Позначимо і Перед діленням на , для зручності, помножимо на 9:

Остача , тому за слід узяти . Далі ділимо на :

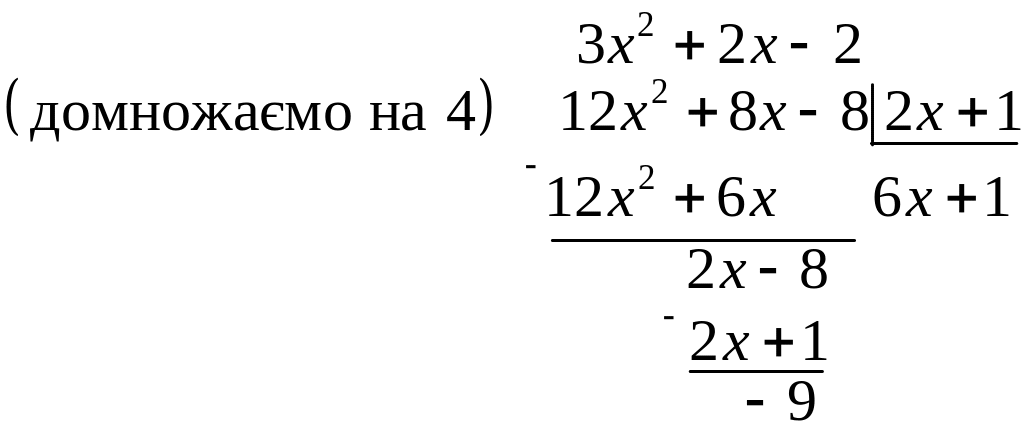
Остача а тобто можна узяти Отже, остаточно маємо:

Введемо поняття числа змін знаків у ряді Штурма. Візьмемо в ряді функцій (67) де - якесь дійсне число. Тоді скінченна послідовність функцій (67) перетворюється в послідовність чисел ,

Число змін знаків у цій послідовності позначатимемо через і називатимемо його числом змін знаків у ряді Штурма в точці .

Приклад 2. Для розглянутого вище многочлена

а) при маємо:

У послідовності чисел , очевидно, дві зміни знаків, тобто

б) при маємо: тобто для цього значення дістаємо одну зміну знаків:

Зауважимо, що при зростанні від до число змін знаків у ряді Штурма змінилося: Як виявиться далі, це пов’язано з тим, що в інтервалі міститься один корінь многочлена