8. Критерій Пірсона (χ2- критерій). Узгодження гіпотези з результатами спостережень.

Критерій узгодженості Пірсона - один з найвідоміших критеріїв χ2, тому його часто і називають просто "критерій хі-квадрат". Використовується для перевірки гіпотези про закон розподілу.

Ґрунтується на групованих даних. Область значень передбачуваного розподілу   ділять на деяке число інтервалів. Після чого будують функцію відхилення ρ по різницях теоретичних імовірностей попадання в інтервали групування й емпіричних частот.

Нехай X=(X1,…, Xn) — вибірка з розподілу  . Перевіряється проста гіпотеза   проти складної альтернативи  . Нехай A1,…, Ak — інтервали групування в області значень випадкової величини з розподілом  . Позначимо для j=1,…,k через νj число елементів вибірки, що потрапили в інтервал Aj: ,

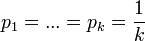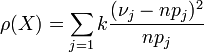і через pj > 0 — теоретичну ймовірність   попадання в інтервал Aj випадкової величини з розподілом  . З необхідністю, p1 + ... + pk = 1. Як правило, довжини інтервалів вибирають так, щоб  . Нехай   (1).

Етапи перевірки статистичних гіпотез

Формулювання основної гіпотези H0 і конкуруючої гіпотези H1. Гіпотези повинні бути чітко формалізовані в математичних термінах.

Задання вірогідності α, що називається рівнем значущості і що відповідає помилкам першого роду, на якому надалі і буде зроблений висновок про правдивість гіпотези.

Розрахунок статистики φ критерію такий, що:

її величина залежить від початкової вибірки  ;

по її значенню можна зробити висновки про істинність гіпотези H0;

сама статистика φ повинна підкорятися якомусь невідомому закону розподілу, так як сама φ є випадковою в силу випадковості  .

Побудова критичної області. З області значень φ виділяємо підмножину   таких значень, по яким можна судити про суттєвість розбіжностей з припущенням. Її розмір вибирається таким чином, щоб виконувалась рівність  . Ця множина   і називається критичною областю.

Висновок про істинність гіпотези. Спостережувані значення вибірки підставляються в статистику φ і по попаданню (або непопаданню) в критичну область   виноситься ухвала про відкидання (або ухвалення) висунутої гіпотези H0.

Областю значень функції (відображення)   називається множина B⊂Y така, що f(X) = B.

Множина Y зовсім не обов'язково збігається з областю значень f. У загальному випадку, B є лише підмножиною Y.

9. Метод найменших квадратів. Пряма регресії.

Метод найменших квадратів — метод знаходження наближеного розв'язку надлишково-визначеної системи. Часто застосовується врегресійному аналізі. На практиці найчастіше використовується лінійний метод найменших квадратів, що використовується у випадкусистеми лінійних рівнянь. Зокрема важливим застосуванням у цьому випадку є оцінка параметрів у лінійній регресії, що широко застосовується у математичній статистиці і економетриці.

Лінійний випадок

Для надлишково-визначеної системи m лінійних рівнянь з n невідомими 

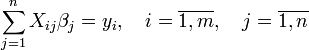
чи в матричній формі запису:

зазвичай не існує точного розв'язку, і потрібно знайти такі β, які мінімізують наступну норму:

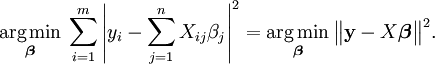
Такий розв'язок завжди існує і він є єдиним:

хоч дана формула не є ефективною через необхідність знаходити обернену матрицю Якщо дано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку економетричну модель, яка б найкраще описувала існуючу залежність. Одним з методів є лінійна регресія. Лінійна регресія передбачає побудову такої прямої лінії, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю пряму одержуємо значення прогнозу. Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої.

16