Випадкова величина. Функція розподілу випадкової величини. Щільність розподілу. Приклади.
Випадковою
величиною є будь-яка (не обов'язково
числова) змінна 
,
"значення" якої 
утворюють множину 
елементарних
подій,
або, іншими словами, позначають точки
в просторі вибірок.
Відповідний розподіл
імовірностей називається
розподілом випадкової величини
. [2]
Множина елементарних подій являє собою можливі значення випадкової величини , називається областю значень цієї величини .
Властивості
Випадкова
величина X — це вимірна функція,
визначена на даному вимірному
просторі 
,
тобто, вона визначається шляхом
зіставлення кожної елементарної
події з
деяким дійсним
числом.
Більш формально:
називається
випадковою величиною, якщо 
,
де 
-- σ-алгебра
Борелевих множин на 
.
Нехай x1, x2,
… — значення випадкової величини X.
Одне і те саме значення xj може
відповідати, взагалі кажучи, різним
елементарним подіям. Множина усіх цих
елементарних подій утворює складену
випадкову подію, що полягає в тому,
що X = xj. Ймовірність цієї події
позначається 
.
Система рівнянь:
визначає розподіл ймовірностей (слід відрізняти від функції розподілу ймовірностей) випадкової величини X.
Очевидно, що:
та 
.
Якщо
дві або більше випадкових величини X1, X2,
…, Xn визначено на одному просторі
елементарних подій, то їх спільний
розподіл задається системою рівнянь,
в яких всім комбінаціям 
, 
і т. д.
призначаються визначені ймовірності.
Випадкові
величини називаються незалежними,
якщо для довільної комбінації значень 
, 
,
…, 
виконується
рівність:
Тобто, якщо Xk залежить лише від k-го випробування, то випадкові величини X1, X2, …, Xn взаємно незалежні.
Ймовірність випадкової величини
Ймовірність випадкової величини дорівнює інтегралу ймовірностей взятому по її області значень:
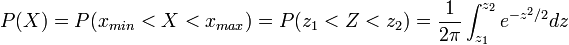
де
; 
—
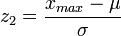граничні значення нормованої величини 
;
—
це середнє
значення величини
;
— cтандартне
відхилення цієї
величини.
Функція розподілу випадкової величини.
Нехай дискретна випадкова величина задана законом розподілу. Розглянемо подію, яка полягає в тому, що випадкова величина Y прийме яке–небудь значення менше будь–якого числа X. Ця подія має певну ймовірність.
xi |
X1 |
X2 |
… |
Xn |
Pi |
P1 |
P2 |
… |
Pn |
Позначимо
При зміні X будуть змінюватися і ймовірності. Отже F(x) можна розглядати як функцію змінної величини X.
Функцією розподілу випадкової величини Y називається функція F(x), яка виражає для кожного X ймовірність того, що Y прийме яке-небудь значення менше заданого.
F(x) – постійна на інтервалах та має скачки в точках, що відповідають її значенням.
Означення
Нехай випадкова величина ξ є абсолютно неперервною, тоді її функція розподілу допускає представлення
,
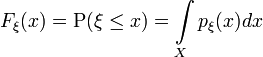де
—
невід'ємна інтегровна
за Лебегом функція,
яка називається функцією густини
імовірності випадкової величини ξ.
Зауваження
Функція густини імовірності існує лише для абсолютно неперервних випадкових величин.
Властивості
,
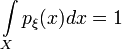
де f(t) — характеристична
функція випадкової
величини ξ.