Уравнение Шредингера.

  В классической механике основной задачей является нахождение ускорения тела в любой момент времени а (t), если известны все силы F(t), действующие на тело:  

В квантовой механике основная задача ставится совершенно иначе. Требуется найти некоторую волновую функцию Ψ(x,y,z), если известно для квантовой частицы, в каком силовом поле она находится. Уравнение для волновой функции Ψ(x,y,z) и называется уравнением Шредингера: .

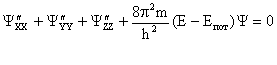Это дифференциальное уравнение второго порядка в частных производных. Здесь: - вторая производная от волновой функции по аргументу – координате Х (аналогично - частные производные по другим пространственным координатам), m- масса частицы, Е - её полная энергия, - потенциальная энергия квантовой частицы. Для электрона в атоме Е_пот = -к * Q / r , где к = 9*10⁹ Н*м²/Кл² - коэффициент пропорциональности в законе Кулона, Q - заряд ядра атома, r - расстояние от ядра. На рис.1 приведен график зависимости потенциальной энергии электрона в атоме от расстояния до ядра.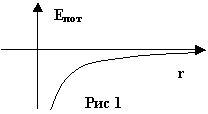

Упрощения.

а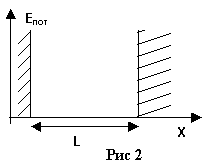 ) Будем рассматривать только одномерный случай (движение только вдоль оси Х). Тогда уравнение упрощается:

(это уже обыкновенное дифференциальное уравнение)

б) электрон может находиться в ограниченной области 0 . Характер зависимости при этом заменяется «прямоугольной ямой» с бесконечными стенками. Внутри «ямы» , вне «ямы» - ¹[1].

Тогда уравнение Шредингера сводится к дифференциальному уравнению:

Запись означает, что волновая функция является функцией, зависящей, от координаты Х. Точно такое же по структуре уравнение было рассмотрено для гармонических колебаний:

Поэтому по аналогии с уравнением гармонических колебаний, для которого решением являлась гармоническая функция: запишем общее решение для уравнения Шредингера:

, где

     и - это так называемые постоянные интегрирования. Их следует найти из граничных условий:

а) следовательно

Отсюда

б)

Отсюда при : или , или

Так как , то

Таким образом, получается условие квантования энергий электрона в атоме.

,где n - главное квантовое число.

Вывод: В отличие от теории Бора полученные условия квантования энергий не требует введения каких либо дополнительных постулатов.

Анализ решения

1). Если подставить в формулу все значения при L = 0,1 м расстояние между уровнями (Е₂ - Е₁) равно 10^-37Дж 10^-16эВ. Такие разности энергий мы просто не воспринимаем и макромир для нас ощущается не дискретным, а непрерывным.

2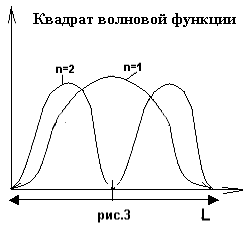 ). При L=10^-10 м аналогично получается Е₂ - Е₁ 4 эВ. Это значение примерно соответствует энергии фотонов видимого света. И мы отчетливо можем различать такие энергии и тем самым можем «отразить» дискретную природу микромира.

3). Вид волновой функции: . Квадрат волновой функции, умноженный на приращение ∆х | *∆х| - характеризует вероятность нахождения частицы в области ∆х. Приведенный на рисунке 3 график представляет характер распределения электронов в потенциальной яме при различных значениях главного квантового числа n. Значение L/2 соответствует по теории Бора первому Боровскому радиусу.