
- •Г.В. Соколовська с.Ю. Соколовський тригонометричні рівняння та нерівності
- •§1 Основні означення та формули тригонометрії
- •Графіки тригонометричних функцій
- •Основні тригонометричні формули
- •1. Формули, що зв’язують тригонометричні функції одного аргументу
- •2. Формули додавання
- •3. Формули зведення
- •4. Формули подвійного аргументу
- •5. Формули, що перетворюють суму і різницю тригонометричних функцій на їх добуток
- •6. Формули, що перетворюють добуток тригонометричних функцій на суму і різницю
- •§2 Обернені тригонометричні функції
- •Графіки обернених тригонометричних функцій
- •§3 Тригонометричні рівняння.
- •Введення допоміжного аргументу.
- •§4 Розв’язування найпростіших тригонометричних нерівностей.
- •Вправи для самостійного розв’язування.
§4 Розв’язування найпростіших тригонометричних нерівностей.
Вправа
30. Розв’язати
нерівність
 .
.
Розв’язання.
При
значеннях
![]() ,
що задовольняють нерівність, відповідні
точки одиничного кола мають ординату
не меншу, ніж
,
що задовольняють нерівність, відповідні
точки одиничного кола мають ординату
не меншу, ніж
![]() .
Множина таких точок – це дуга кола
.
Множина таких точок – це дуга кола
![]() (рис.
12), всі точки якої знаходяться не нижче
прямої
(рис.
12), всі точки якої знаходяться не нижче
прямої
![]() .
Точка
.
Точка
![]() має
ординату
має
ординату
![]() і належить
правому півколу, тому в якості відповідного
значення аргументу
і належить
правому півколу, тому в якості відповідного
значення аргументу
![]() слід
взяти значення
слід
взяти значення
 .
.

Тепер
треба уявити собі, що ми здійснюємо
обхід дуги
![]() від точки
від точки
![]() до
точки
до
точки
![]() проти
ходу годинникової стрілки. Тоді
проти
ходу годинникової стрілки. Тоді
![]() і, легко зрозуміти, що
і, легко зрозуміти, що
 .
Таким
чином, отримано такі розв’язки нерівності
.
Таким
чином, отримано такі розв’язки нерівності
 .
Але
до цього моменту
розв’язки
шукали лише на проміжку
.
Але
до цього моменту
розв’язки
шукали лише на проміжку
 ,
який має довжину
,
який має довжину
![]() .
Завдяки
періодичності синуса, всі інші розв’язки
утворюють додаванням до вже знайдених
розв’язків чисел виду
.
Завдяки
періодичності синуса, всі інші розв’язки
утворюють додаванням до вже знайдених
розв’язків чисел виду
![]() .
Одержимо
відповідь:
.
Одержимо
відповідь:
 .
.
Вправа
31. Розв’язати
нерівність
 .
.
Розв’язання.
На
рисунку 13 зображено дугу
![]() одиничного
кола, яка лежить нижче прямої
одиничного
кола, яка лежить нижче прямої
 .
Точки
.
Точки
![]() та
та
![]() не входять до множини, що розглядається,
оскільки їх ординати дорівнюють
не входять до множини, що розглядається,
оскільки їх ординати дорівнюють
![]() .
Легко бачити, що
.
Легко бачити, що
 .
Обходимо дугу
.
Обходимо дугу
![]() від точки
від точки
![]() до
до
![]() за годинниковою стрілкою.
за годинниковою стрілкою.

Тоді
 .
Всі розв’язки нерівності з проміжку
.
Всі розв’язки нерівності з проміжку
 довжини
довжини
![]() будуть такими:
будуть такими:
 .
.
Враховуючи
періодичність синуса отримаємо всі
розв’язки нерівності:
 .
.
Вправа
32. Розв’язати
нерівність
 .
.
Розв’язання.

На
рисунку 14 зображено дугу
![]() одиничного
кола, яка лежить праворуч від прямої
одиничного
кола, яка лежить праворуч від прямої
 .
Точки
.
Точки
![]() та
та
![]() належать множині, що розглядається. Як
бачимо,
належать множині, що розглядається. Як
бачимо,
 .
Обходимо дугу за годинниковою стрілкою.
Тоді
.
Обходимо дугу за годинниковою стрілкою.
Тоді
 .
Враховуючи періодичність косинуса,
одержимо відповідь:
.
Враховуючи періодичність косинуса,
одержимо відповідь:
 .
.
Вправа
33. Розв’язати
нерівність
![]() .
.
Розв’язання.

Період
тангенса дорівнює
![]() .
Тому знайдемо спочатку всі розв’язки
нерівності, що належать інтервалу
.
Тому знайдемо спочатку всі розв’язки
нерівності, що належать інтервалу
 ,
а потім скористаємось періодичністю
тангенса. Побудуємо лінію тангенсів.
Якщо
,
а потім скористаємось періодичністю
тангенса. Побудуємо лінію тангенсів.
Якщо
![]() є розв’язком нерівності, то відповідна
точка
є розв’язком нерівності, то відповідна
точка
![]() лінії тангенсів повинна мати ординату,
що не перевищує
лінії тангенсів повинна мати ординату,
що не перевищує
![]() .
Відповідна дуга
.
Відповідна дуга
![]() (з
кінцями в точках
(з
кінцями в точках
![]() та
та
![]() )
зображена на рисунку 15. Зауважимо, що
точка
)
зображена на рисунку 15. Зауважимо, що
точка
![]() належить,
а
належить,
а
![]() не
належить множині, що розглядається. Як
бачимо
не
належить множині, що розглядається. Як
бачимо
 .
Обходячи
дугу
.
Обходячи
дугу
![]() за годинниковою стрілкою, одержимо всі
розв’язки з інтервалу
за годинниковою стрілкою, одержимо всі
розв’язки з інтервалу
 .
Вони будуть такими:
.
Вони будуть такими:
 .
Враховуючи періодичність тангенса,
отримаємо відповідь:
.
Враховуючи періодичність тангенса,
отримаємо відповідь:
 .
.
Вправа
34. Розв’язати
нерівність
![]() .
.
Р озв’язання.
озв’язання.
Запишемо
нерівність у вигляді
 .
Побудуємо лінію котангенсів. Відповідна
дуга
.
Побудуємо лінію котангенсів. Відповідна
дуга
![]() (з
кінцями в точках
(з
кінцями в точках
![]() та
та
![]() )
зображена на рисунку 16. Тоді
)
зображена на рисунку 16. Тоді
 ,
а
,
а
![]() .
.
Одержимо:
 або
або
 .
.
Відповідь:
 .
.
Вправа
35. Розв’язати
нерівність
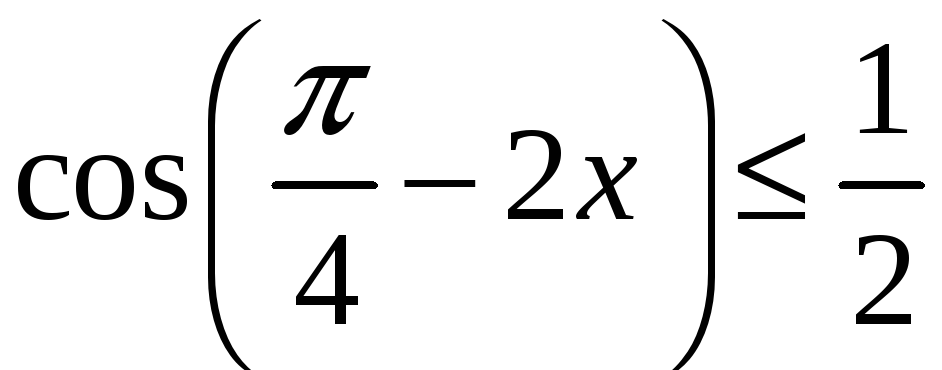 .
.
Розв’язання.
Відповідна
дуга
![]() (з
кінцями в точках
(з
кінцями в точках
![]() та
та
![]() ),
що зображена на рисунку 17, обходиться
проти ходу годинникової стрілки.
),
що зображена на рисунку 17, обходиться
проти ходу годинникової стрілки.
Як
бачимо,
 ,
а
,
а
 .
.

Отже
аргумент косинуса
 задовольняє нерівність:
задовольняє нерівність:
 .
.
Звідки
маємо:
 або
або
 .
Замінивши в остаточній відповіді
.
Замінивши в остаточній відповіді
![]() на
на
![]() ,
отримаємо:
,
отримаємо:
 .
.
Вправи для самостійного розв’язування.
![]() Обчислити:
Обчислити:
-
а)
 ;
б)
;
б)
 .
. -
а)
 ;
б)
;
б)
 :
в)
:
в)
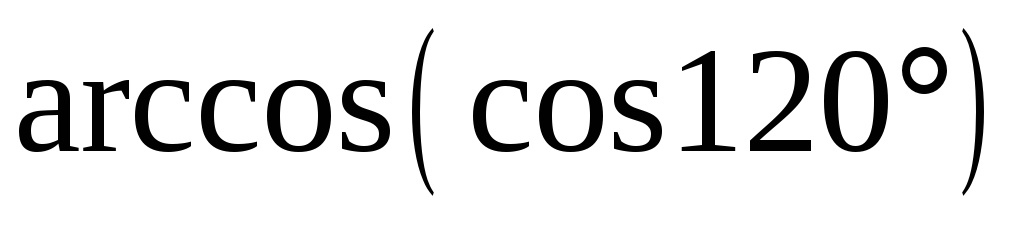 ;
г)
;
г)
 ;
д)
;
д)
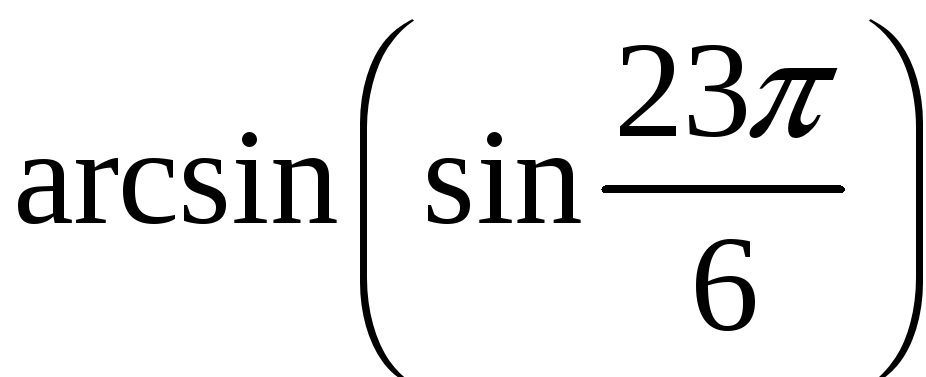 ;
е)
;
е)
 ;
э)
;
э)
 ;
ж)
;
ж)
 .
. -
а)
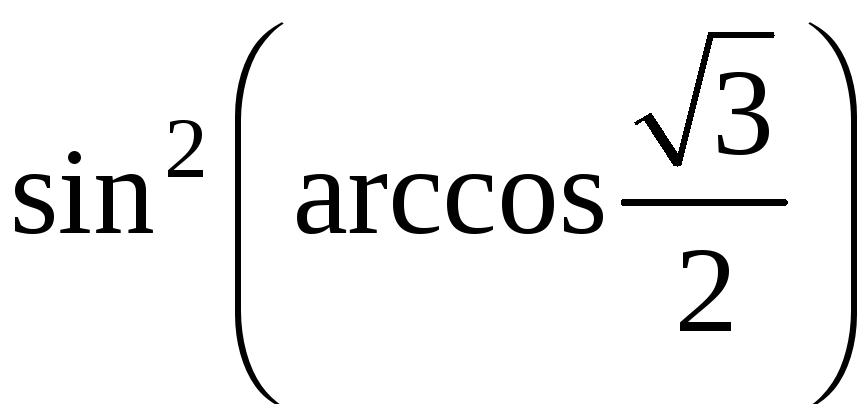 ;
б)
;
б)
 :
в)
:
в)
 ;
г)
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
 ;
э)
;
э)
 ;
ж)
;
ж)
 ;
з)
;
з)
 .
.
![]() Довести тотожність:
Довести тотожність:
-
а)
 ;
б)
;
б)
 .
.
![]() Розв’язати
рівняння:
Розв’язати
рівняння:
-
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
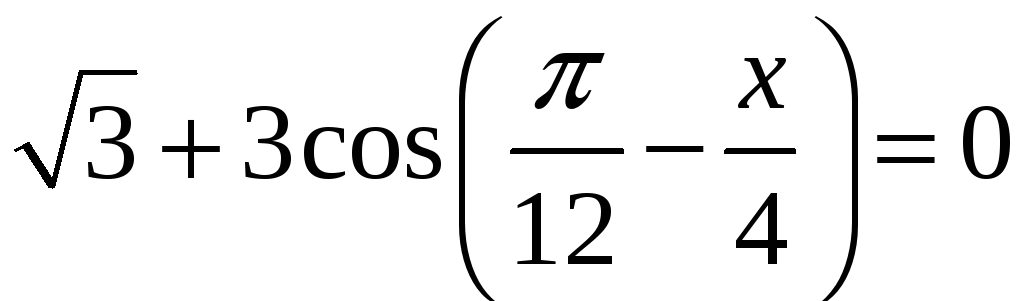 .
. -
а)
 ;
б)
;
б)
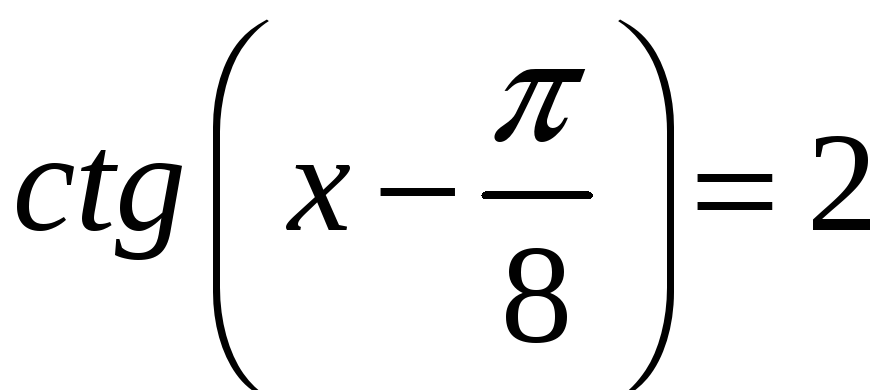 ;
в)
;
в)
 .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
д)
;
д)
 е)
е)
 ;
э)
;
э)
 ;
ж)
;
ж) .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
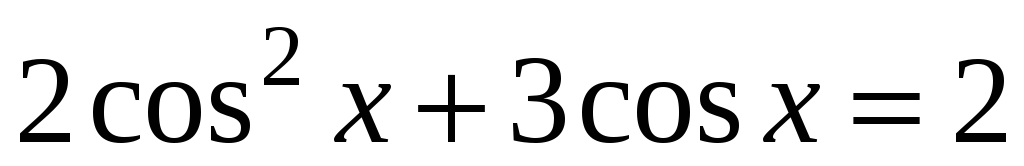 ;
г)
;
г)
 ;
д)
;
д)
 е)
е)
 ;
э)
;
э)
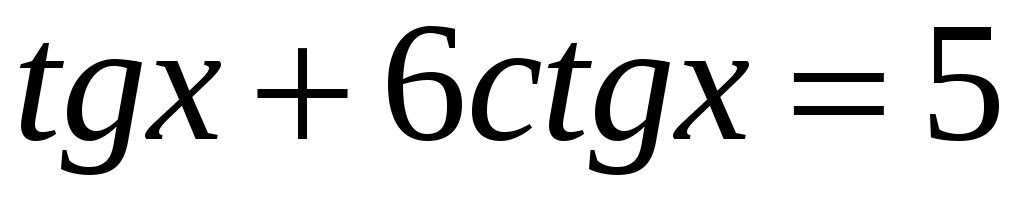 ;
ж)
;
ж)
 .
. -
а)
 ;
б)
;
б)
 .
. -
а)
 ;
б)
;
б)
 .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
д)
;
д)
 .
.
-
Застосувати універсальну тригонометричну підстановку а)
 ;
б)
;
б)
 ;
в)
;
в) .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
-
а)
 ;
б)
;
б)
 ;
в)
;
в)
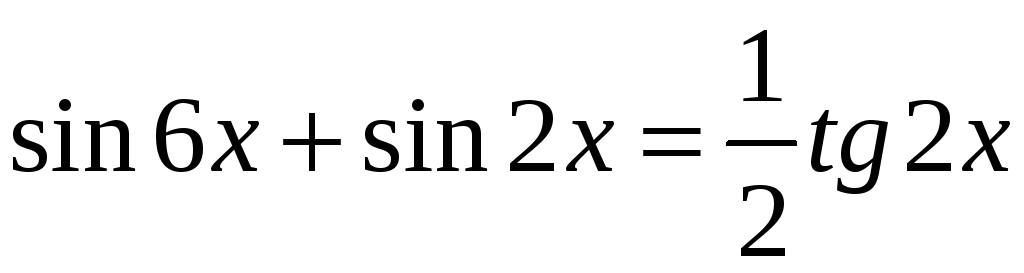 ;
г)
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
 .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
д)
;
д)
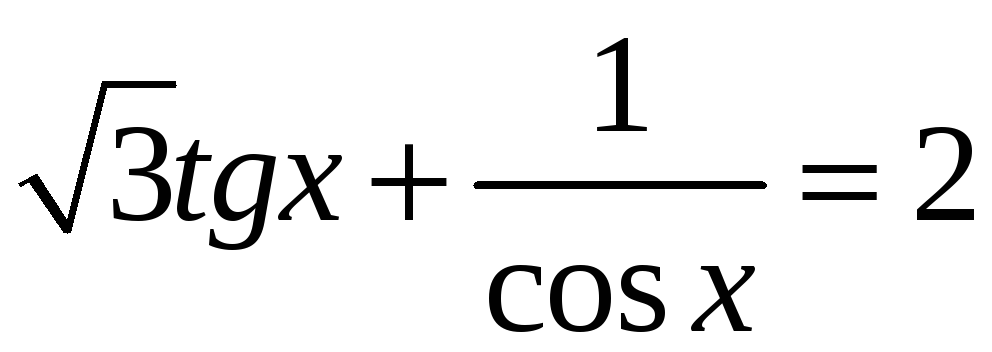 .
. -
а)
 ;
б)
;
б)
 .
.
![]() Розв’язати
нерівність:
Розв’язати
нерівність:
-
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
а)
 ;
б)
;
б)
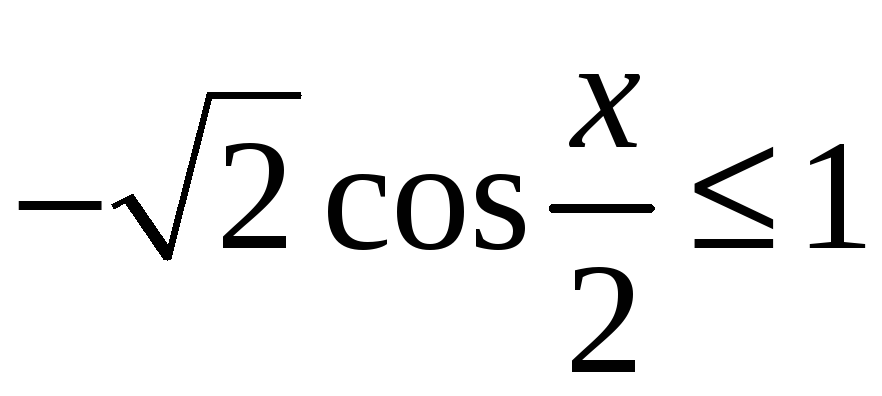 ;
в)
;
в)
 .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
